前の記事からの続きだが, 文章題の話ではないのでタイトルを改めた. 倍概念 (「量」に対する数の倍作用と言うべきものである) を使って分数を説明することもできる. 以下はその概略である.
1) 単位分数
n は (0 でない) 整数とする. 量 A が量 B の n 倍と同じであるとき, 量 B は「量 A の 1/n」という.
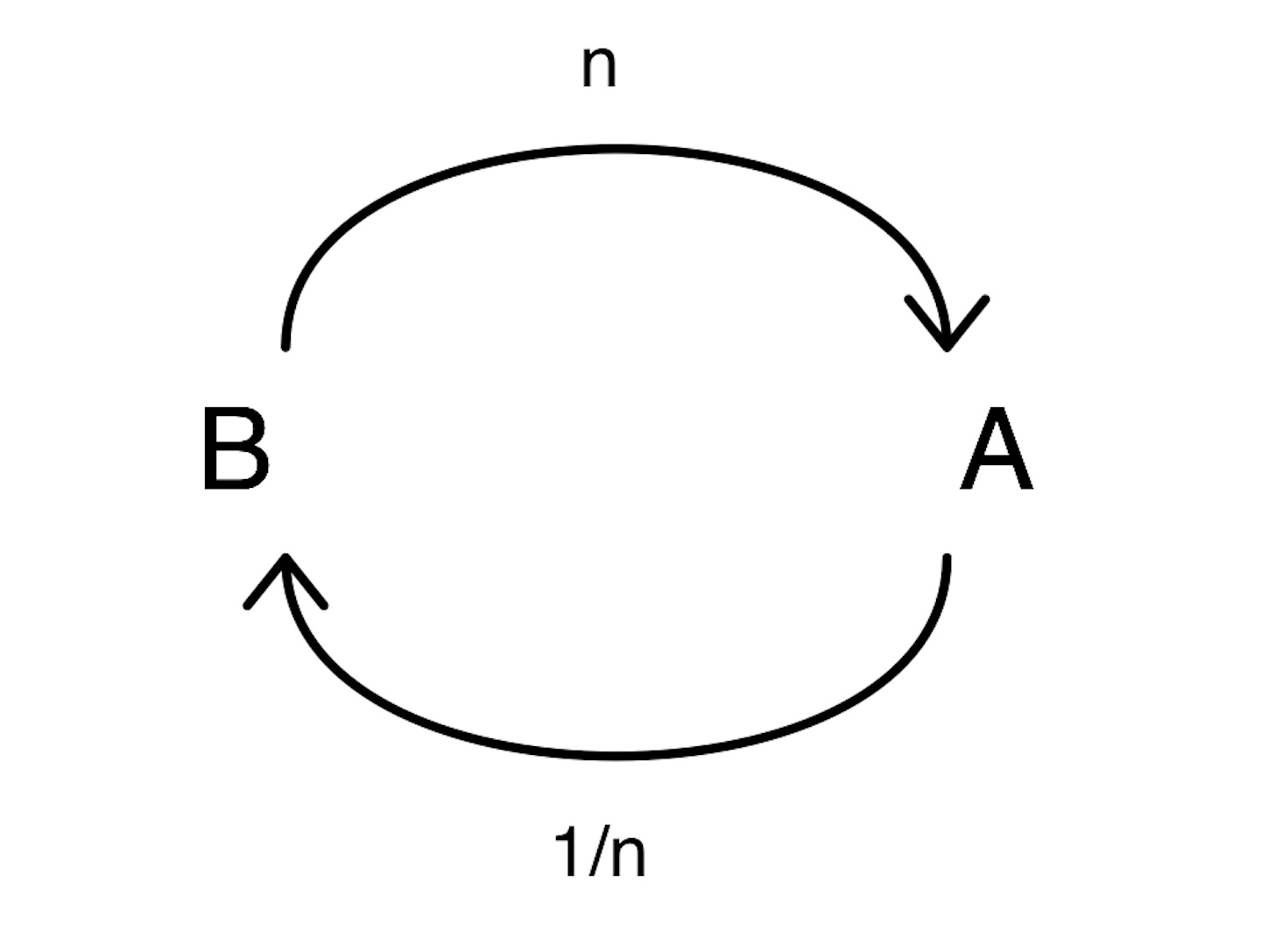
※ これは小学校 2 年生で習う. (分数は小学校で 5 年にわたって習うのである!) //
2) 一般の分数
量 A と量 B の大きさを比較するのに第 3 のある量 C があって,
A は C の p 倍である.
B は C の q 倍である.
が同時に成り立つとする (C が存在しない場合は無理数*1を考えないといけないが, もちろん無理数は算数の範囲外である). 後者から C は 「B の 1/q」だから, 前者に代入して C を消去すると,
A は「B の 1/q」の p 倍である.
これを簡単に,
A は B の p/q 倍である.
というが, 気をつけないといけないのは単位量は「B の 1/q」ということである. (倍は整数の範囲で考えて, 端数は単位量の方にくりこんでしまう方が説明が簡単だし, 想像しやすい. なお, このような単位を「部分単位」と呼ぶことがある. 「普遍単位」と区別するためだと思う. なお, 数を整数の範囲で考える理由について, 別の言い方をすれば,「数」がまだ整数に過ぎなかった頃の, 稚ない, しかしどこか湿った郷愁を煽りたてる原風景を虚構として考えてみたいということである.)
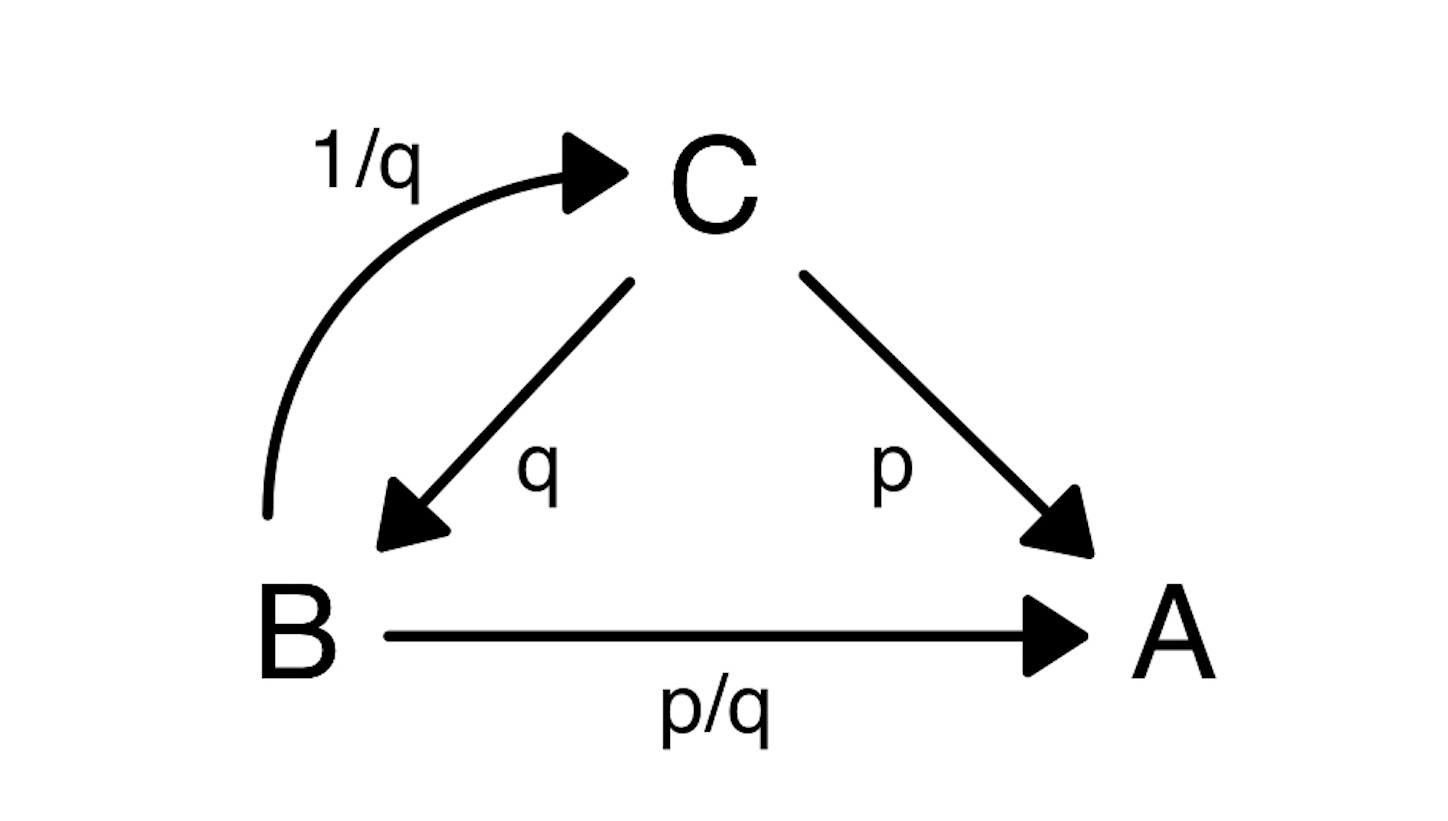
※ 比で表せば, A : B = p : q ということである. //
※ B は A の q/p 倍であり, 逆数の関係になっている. //
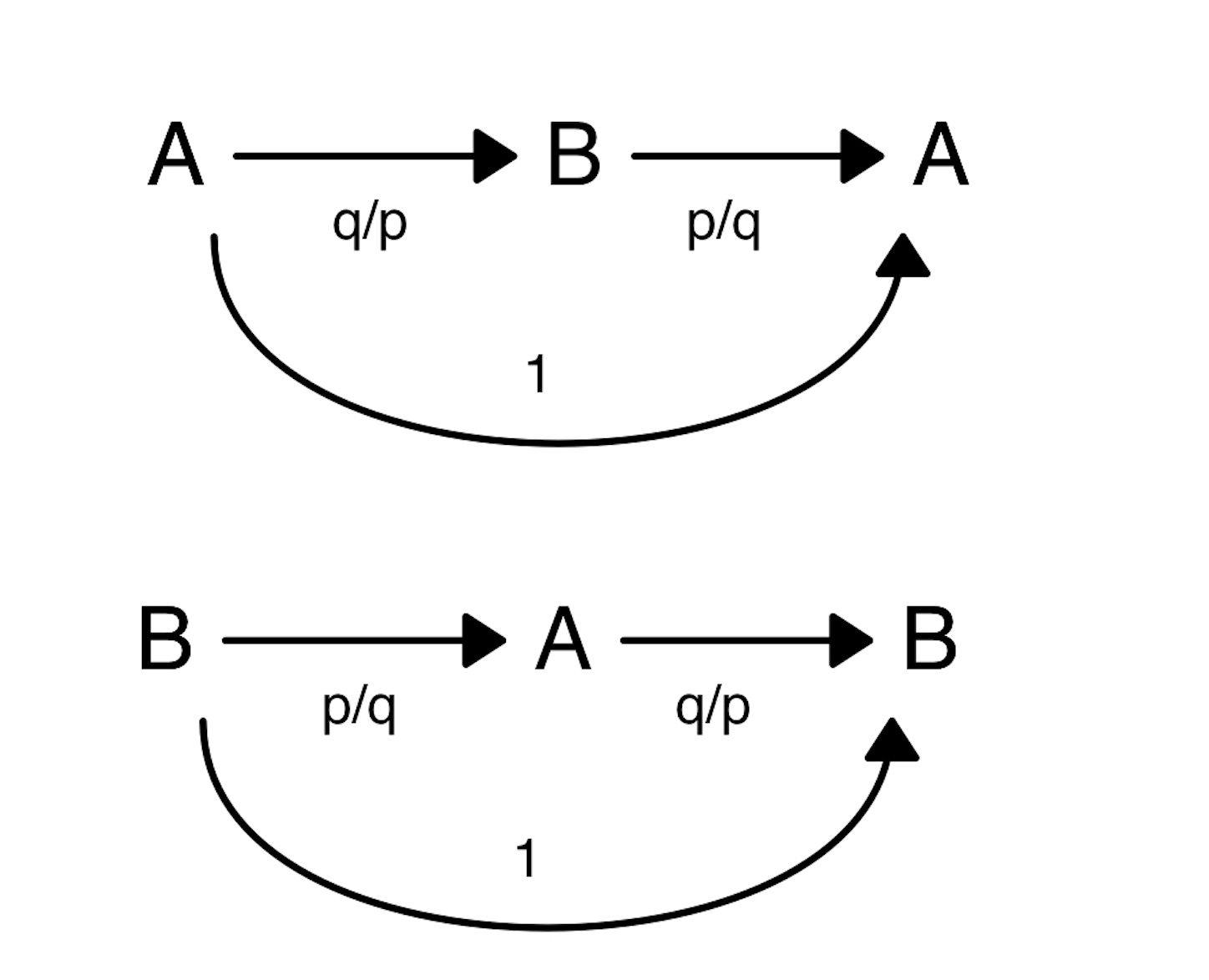
※ 注として, 仮定より A の q 倍は B の p 倍に等しい. したがって, A は「B の p 倍の 1/q」である. つまり,「B の 1/q」の p 倍 と「B の p 倍の 1/q」は同じ大きさである. (最大公約数と最小公倍数の存在 *2 がこの交換を保証することで分割分数と商分数の観点は統合される.) //
※ 量分数というのは, B として “1 m” (本当は単に “m” でよいのだが) のような普遍単位 (量) をとったものである. 「1 m の 1/q」という部分単位は “1/q m” と表される. 直前に述べたことにより, たとえば 2/5 m = 1 m × 2 ÷ 5 という商分数の定義 (5 年生で習う) は, 今まで習った 1/5 m × 2 と一致する. 別の見方をすれば, 1 m × 2 ÷ 5 = 1 m ÷ 5 × 2 のように ÷ と × のどちらでも先に計算してよいから という対等な表記が適しているといえるのかもしれない. //
ところで C の取り方には任意性がある. つまり C の 1/2, 1/3, … をとっても A と B の大きさの比較は可能であるから, これらを同一視する必要があり, 通常は (しばしば審美的, 慣習的な理由により) 互いに素な p, q を代表にとって表わす. (単位の取り方により測定値は変わるのである.)
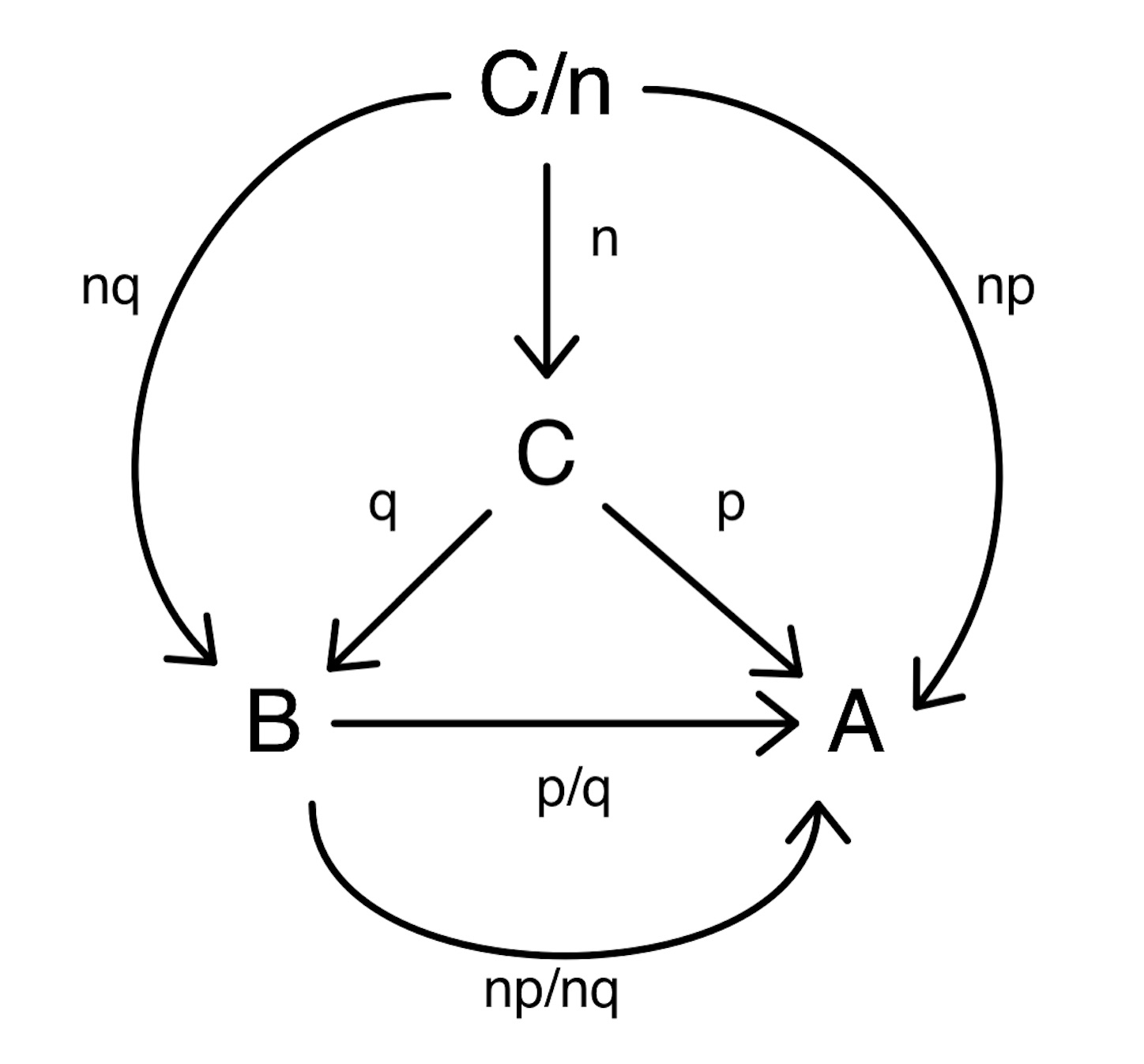
また分数同士の大小関係は, 分母 (下のわる数字のこと) と分子 (上のかける数字のこと) のどちらかを揃えれば比較できる. 分母と分子に同じ自然数をかけて, 同値な (同じ類に属する) 分数を作ることを「倍分」と呼ぶ. 通常は分母の方を揃えるので, この操作を「通分」という特別な名称で呼ぶ.
※ a/b と c/d が等しいとき, ad/bd と bc/bd を比較して ad = bc となる. 逆も明らかに成立つ. (比でいう「内項の積と外項の積は等しい」が比が等しいことの同値な言い換えであることに相当する.) //
3) 分数のたし算•ひき算
通分すれば単位量が同じになるので, たし算が可能になるのは, 通常の倍計算と同じである. またひき算はたし算の逆計算である.
4) 分数のかけ算
これは, A が B の n/m 倍, B が C の q/p 倍のとき A は C の何倍かを求めることである.
きちんと書けば,
A が「B の 1/m」の n 倍, B が「C の 1/p」の q 倍のとき A は C の何倍かを求めることである.
さらにいいかえて (倍分して),
A は「B の 1/mq」の nq 倍である.
B は「C の 1/mp」の mq 倍である.
後者から「B の 1/mq」は「C の 1/mp」と等しいことがわかるから, 前者より,
A は「C の 1/mp」の nq 倍になる. すなわち,
A は C の nq/mp 倍である.
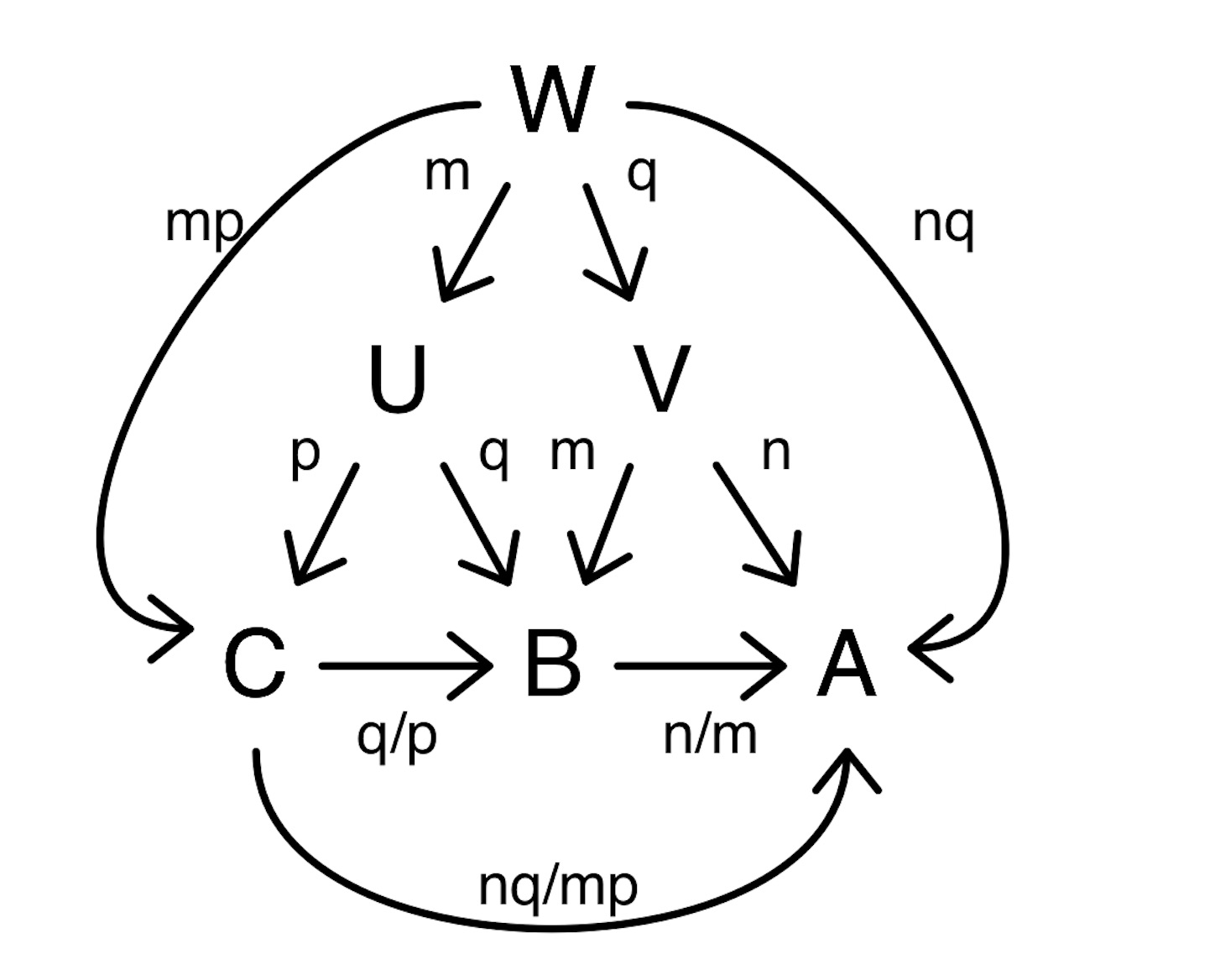
※ ようするに連比計算をすればよいのである.
A : B = n : m, C : B = p : q だから,
A : B : C = nq : mq : mp
したがって, A : C の比の値は nq/mp である. //
5) 分数の割り算
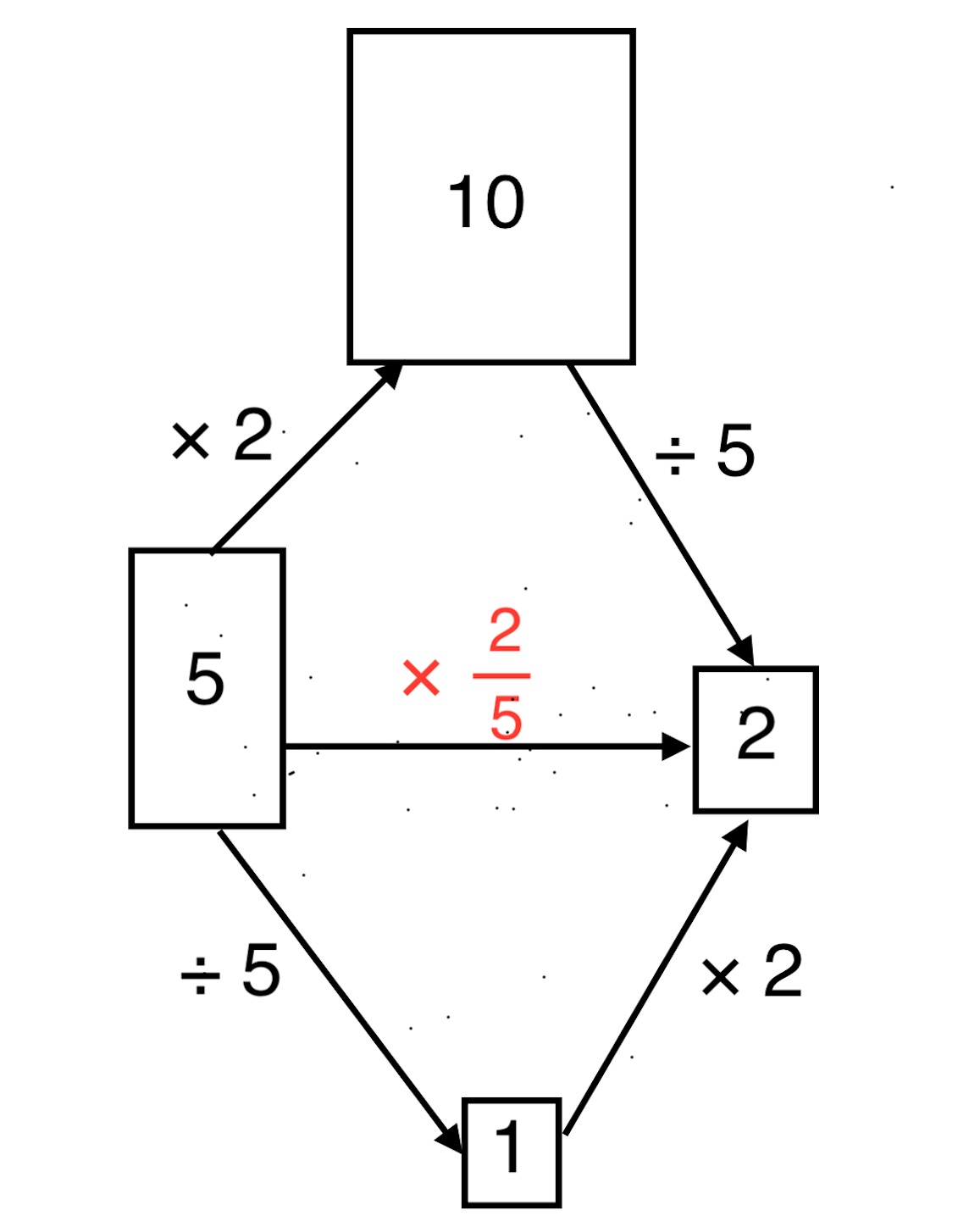
まず, x の q/p 倍が n/m であるとき, x を求める. (算数用語で, 「等分除」と呼ばれたりする. つまり (単位 × a) ÷ b のことである.)
※ なお, ここでは “m”, “L", “kg” などの (普遍) 単位を “1” で表わすことにする. 以前にも書いたが「単位」は単なる名前などではなく, 測定 (単位の何倍かを決めることに他ならない) の比較基準となるある「量」そのものを表わしている. 一方「何倍」の「何」が「数」である. 単位の測定は単位の 1 倍である.//
「n/m の 1/q」は「x の 1/p」 に等しい.
「n/m の 1/n」は「1 の 1/m」 に等しい.
つまり,
「n/m の 1/nq」は「x の 1/np」 に等しい.
「n/m の 1/nq」は「1 の 1/mq」に等しい.
したがって「x の 1/np」が 「1 の 1/mq」 に等しい. すなわち x は「1 の 1/mq」の np 倍, つまり 1 の (np/mq = n/m × p/q ) 倍である.
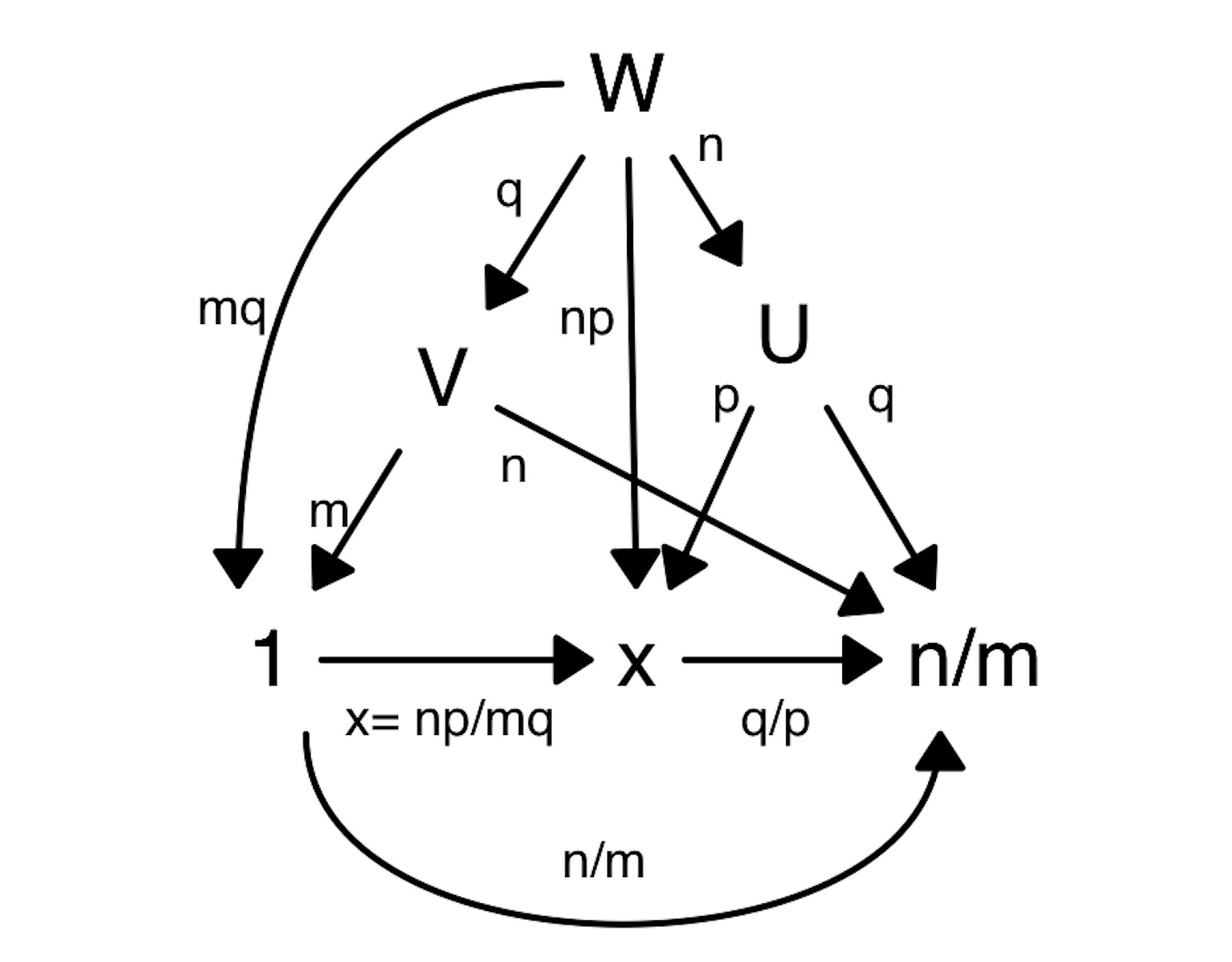
※ 連比だと,
1 : n/m = m : n, x : n/m = p : q から,
n/m : x : 1 = nq : np : mq
だから, x = np/mq
//
※ 下の図のようにみれば, かけ算はすでに求まったので, 直ちにわかる.
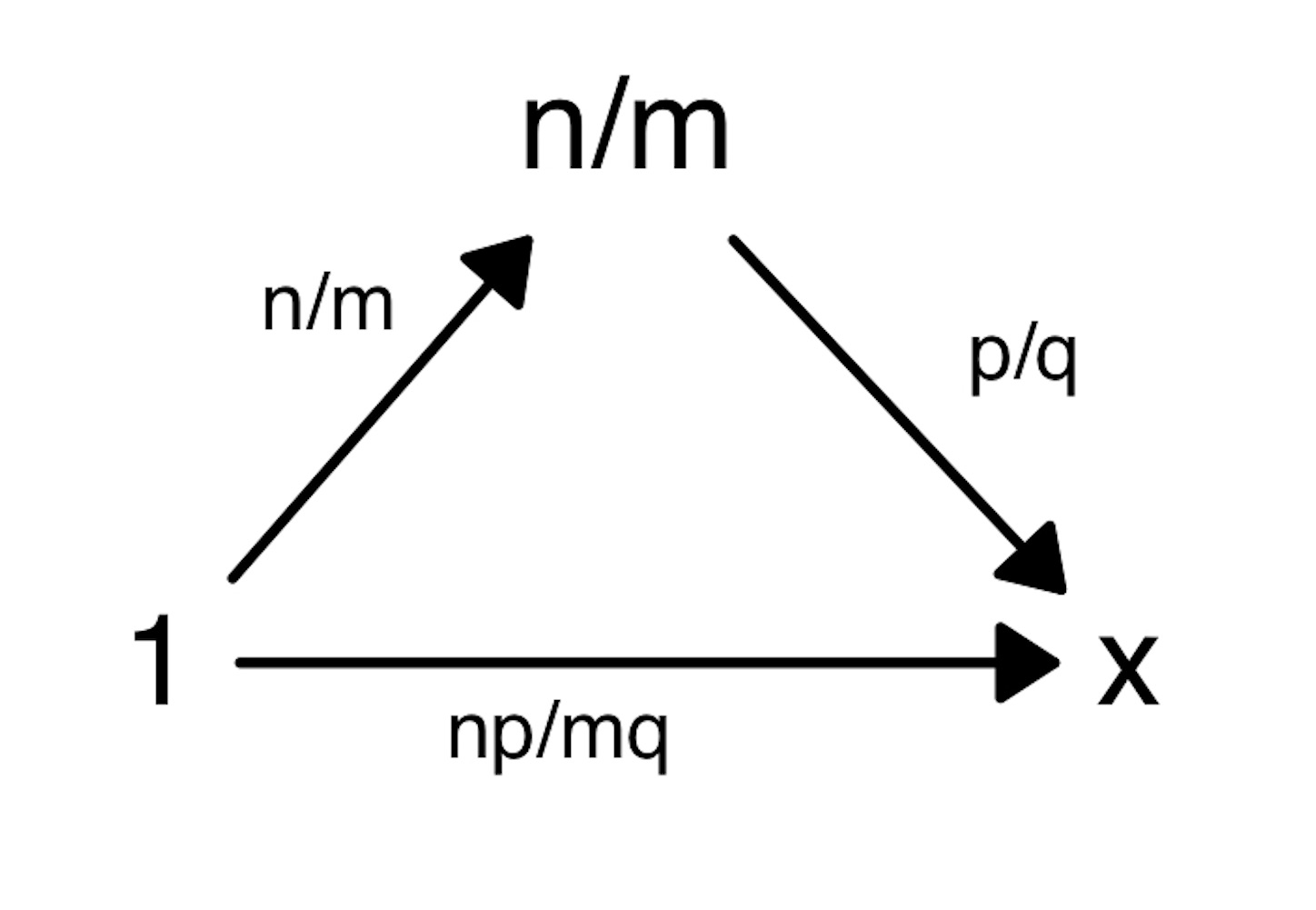
//
つぎに, q/p の x 倍が n/m であるとき, x を求める. (算数用語で, 「包含除」と呼ばれたりする. つまり, (単位 × a) ÷ (単位 × b) = a ÷ b のことである*3.)
「n/m の 1/n」は「1 の 1/m」に等しい.
「q/p の 1/q」は「1 の 1/p」に等しい.
つまり,
「n/m の 1/np」は「1 の 1/mp」に等しい.
「q/p の 1/mq」は「1 の 1/mp」 に等しい.
したがって,
「n/m の 1/np」は 「q/p の 1/mq」に等しい.
つまり,
「q/p の 1/mq」の np 倍が n/m だから,
x は np/mq である.
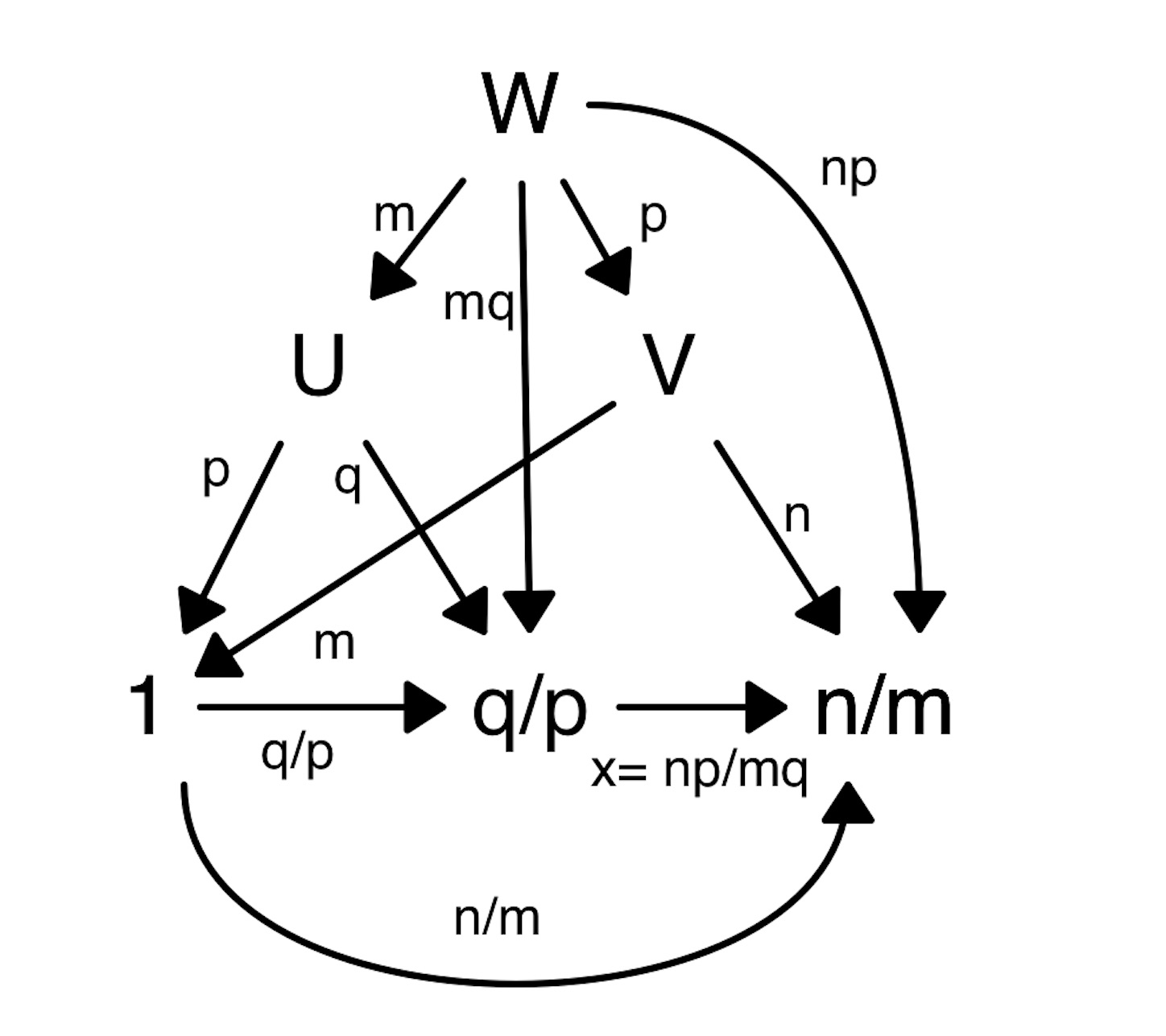
※ 連比だと,
1 : q/p = p : q
1 : n/m = m : n
だから,
n/m : q/p : 1 = np : mq : mp
したがって,
n/m : q/p = np/mq
//
※ 先程と同様, 以下のように見れば直ちに求まる.
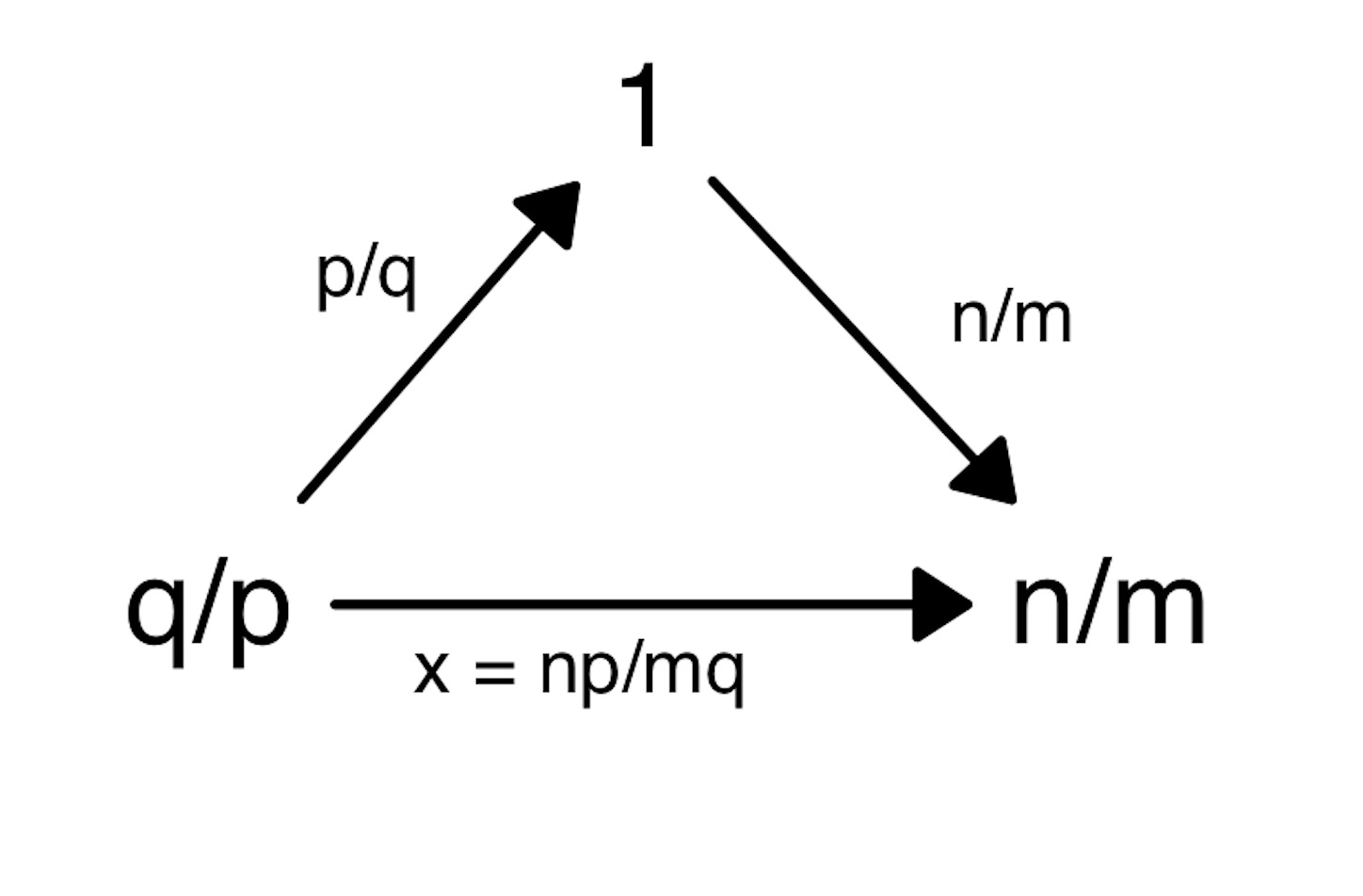
//
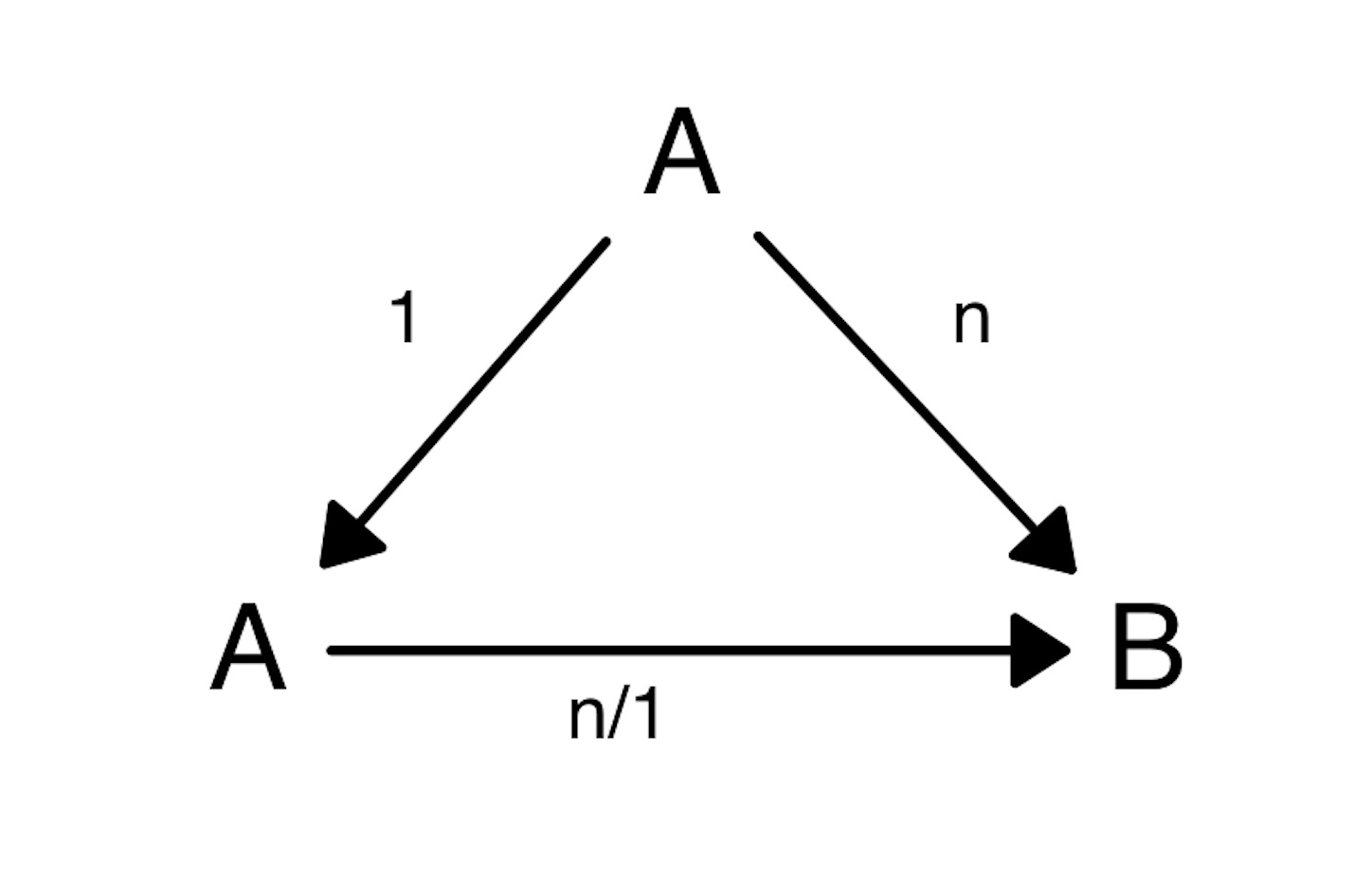
※ 商分数の証明
下の図から明らかなように, 整数 n は, n/1 と等しい.
分数の割り算がわかったので,
a ÷ b = a/1 ÷ b/1 = a/b
となる.
//
※ 小数は分数に帰着できるといってしまえばそれまでだが,「小数の倍」は少し発想が違う. 小数の倍は, A を B を基準にして比較する場合に, B の整数倍であまりがでたら, そのあまりを「B の 1/10」で倍を測り, それでもあまりがでたら 「B の 1/100」 で倍を測ることを以下続けていくという極限に通じる方法であり, これは素直に了解できると思う. なお, 小数の場合は分母には素因数が 2 と 5 の分数しか使わないのだから, 既約分数で分母に 2 と 5 を除く素因数があれば通分しても当然 10 の累乗にできないから循環小数になる. (なお, もう一つの量の比較の仕方として連分数による方法があるが省略する.) //
*1:無理数を表わす英語の “irrational number” は「整数の比 (ratio) で表わすことができない (実) 数」という意味である. 有理数は「稠密」であるが「完備」ではない.
*2:最大公約数の存在はユークリッド互除法により保証されるし, 最小公倍数は自然数の空でない集合が最小値をもつという原理から公倍数が存在することさえ言えればよい.
*3:ここで, 「単位 ÷ 単位 = 1」は, 数の計算の ÷ を量に適用しているので間違いであり, 本当は双対基底の みたいな議論から始めて, (線型空間の) テンソル積
の縮約にまで言及することが必要だとは思うが, ここでは深入りしない. 量を単位が基底となる線型空間として考え, テンソル積
を使うと, たとえば「面積」は, (タテの長さ)
(ヨコの長さ) という (2, 0) テンソルの同型として, 「速さ」は (距離)
(時間)* という (1, 1) テンソルの同型として計算の意味合いをもっと明確にできる. 秒*(3秒) = 3 であるから, 秒* は, (3 秒) から係数を取り出すことで, (3 秒) という時間を「秒」という単位で測定していると解釈できる. (3秒)*(3秒) は 3 秒を単位として, 3 秒を測定するのだから 1 であり, このことから, (3秒)* = (1/3) × 秒* である. 「速さ」は正比例という関数で, (時間, 距離) について分数のような同値関係 ——(時間の k 倍, 距離の k 倍) も同値 ——をもつが, 時間を双対な (時間)* に移せば, ( (時間)*, 速さ) はテンソル積の同値関係を満たすのである. ここでテンソル積の同値関係とは, たとえば, ( (時間)* の k 倍, 距離) は ( (時間)*, 距離の k 倍) と同値というようなことどもである (面積が等しい長方形のタテ, ヨコの長さの組すべてを同じ類に入れるようなことどもである).