年理科の入試問題から. いままでの延長で解ける. ところで, 秋山武太郞先生の本を読むとコンパスのことが「兩脚器」と書いてあった.
【問】

【解】
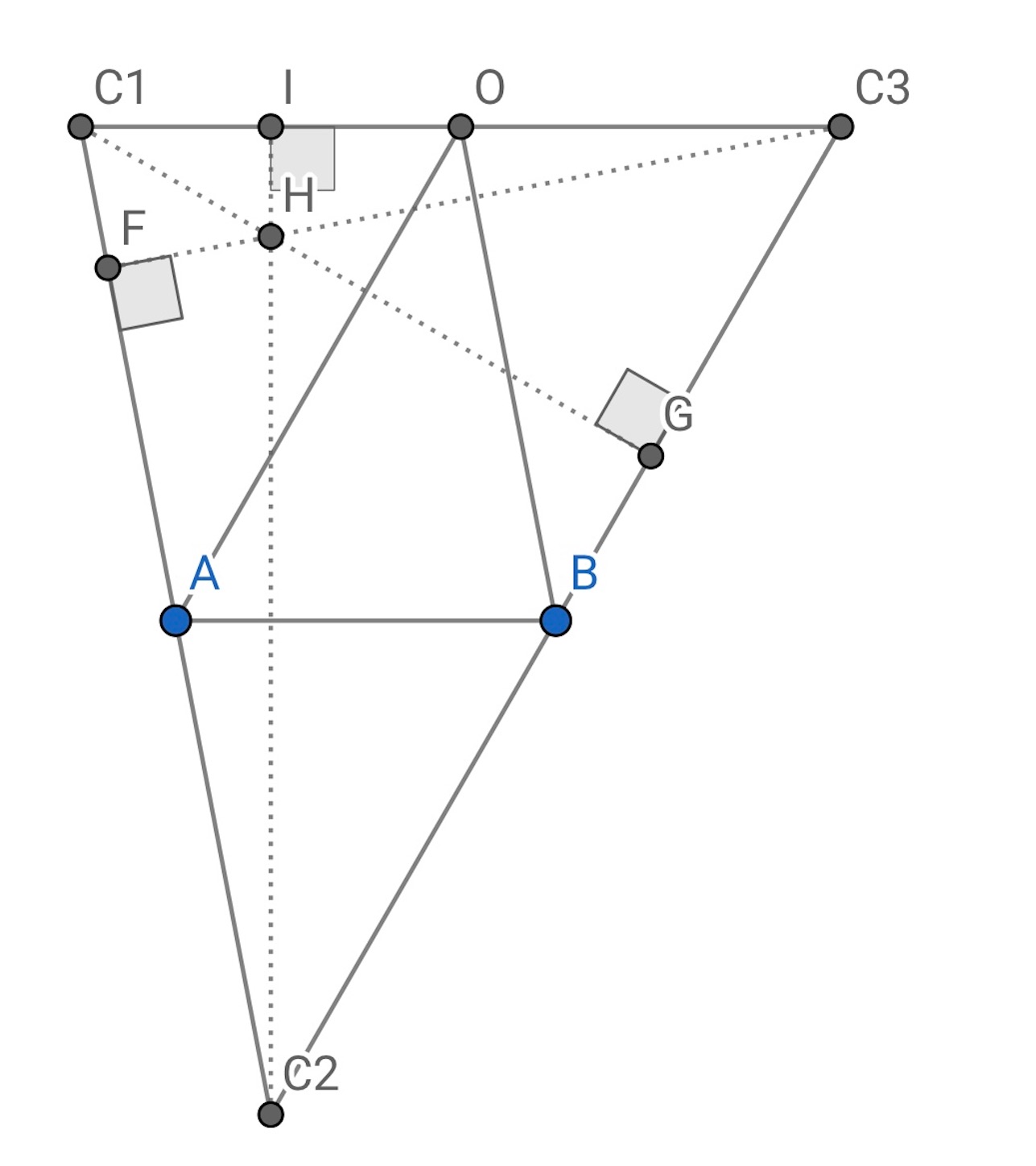
(1) 展開図を書くと の
つの辺 (
,
,
) の中点を結んだものが
になっている. 垂線の足
は, 前の記事でやったように,
から辺
,
から辺
,
から辺
に下ろした垂線の交点であり,
の垂心である.
とおいて,
から, で
.
とおいて,
から, . したがって,
.
天秤法により,
と求まる. したがって,
であるが, あとは と
を
と
で表す計算をひたすらやれば,
となる.
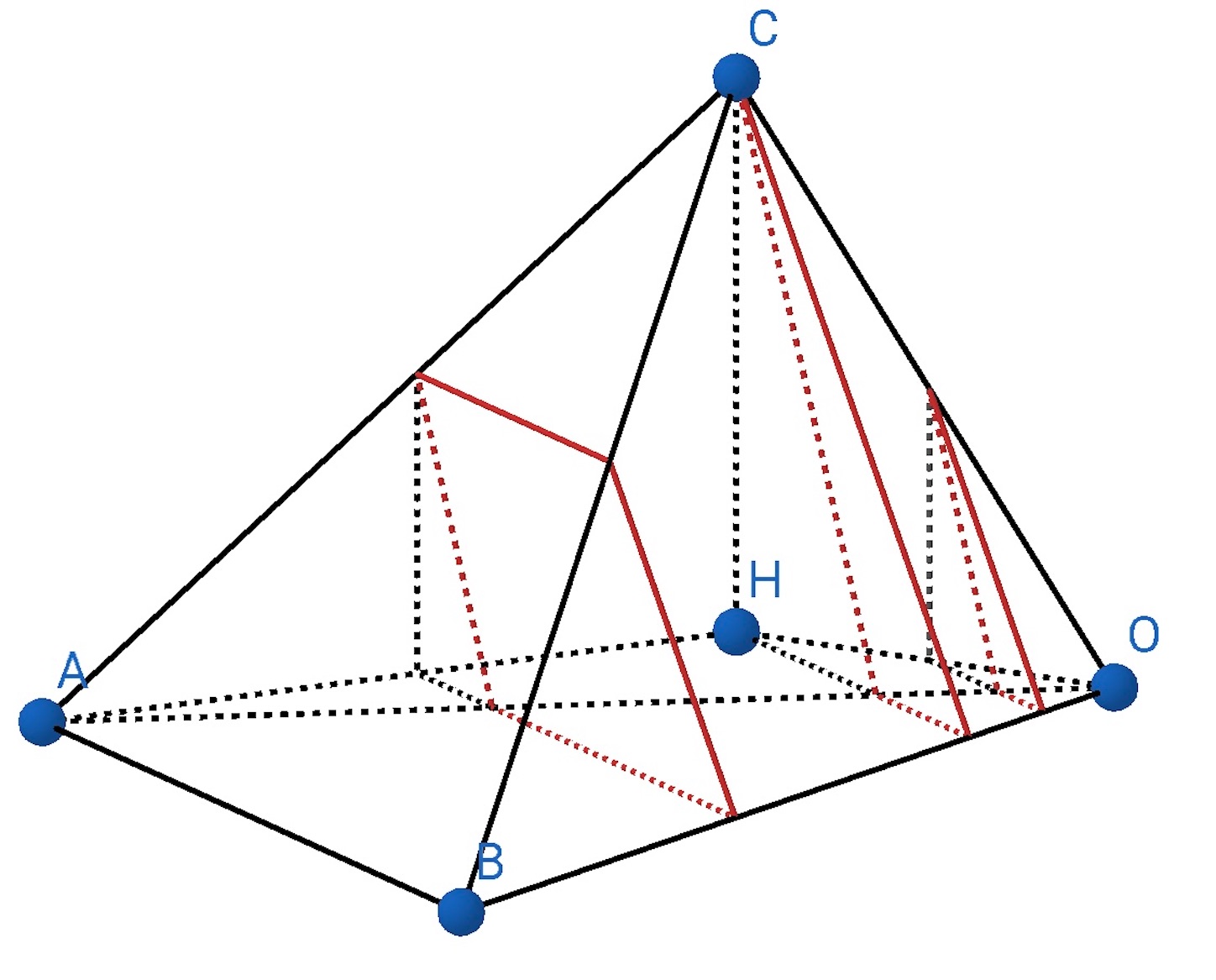
まず切り口の平面が, 頂点
を含むときがすぐに作図できる. 他のところの切り口は、この切り口に平行である (
つの平行平面は, これに交わるどんな直線も同じ比に分けるという定理がある. これは平行
平面を第
の平面で切れば, その
つの交線は平行であるということと, 平面幾何の平行線の比例の定理からの帰結である).
まず, を求める.
とおいて, 方べきの定理より,
から, . したがって,
から,
に下ろした垂線の足を
とすると
以上から,
のとき, 切り口は三角形で, 底辺は
, 高さ
は,
から,
したがって, 面積は,
である.
次に のとき, 切り口は台形で, その下底の長さは,
, 上底の長さ
は,
から, となる. また高さ
は,
から,
以上より,
(3)
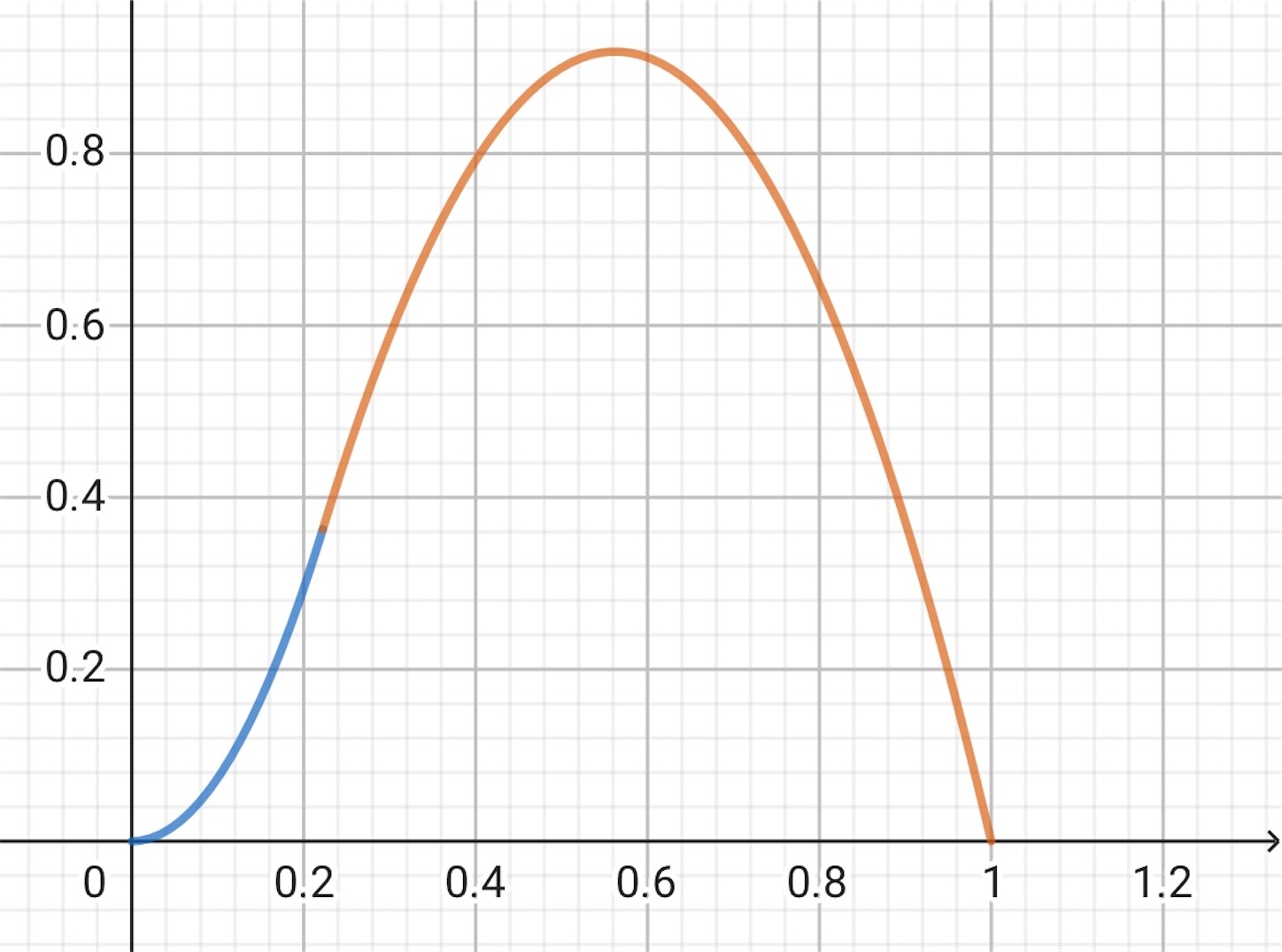
最大値は, 切り口が台形の場合で, のとき,
となる.
//