同一法 - ノリの悪い日記

同一法による証明の例. 下の図のように直角三角形 $ABC$ の斜辺 $BC$ の中点を $D$ とするならば $AD = BD$ というのをわざわざ同一法を使って証明してみる. 円周角は中学 $3$ 年生にならないと習わない. (ただ, 平行四辺形の特別な場合である長方形の対角線を考えればすぐにわかることではある.)

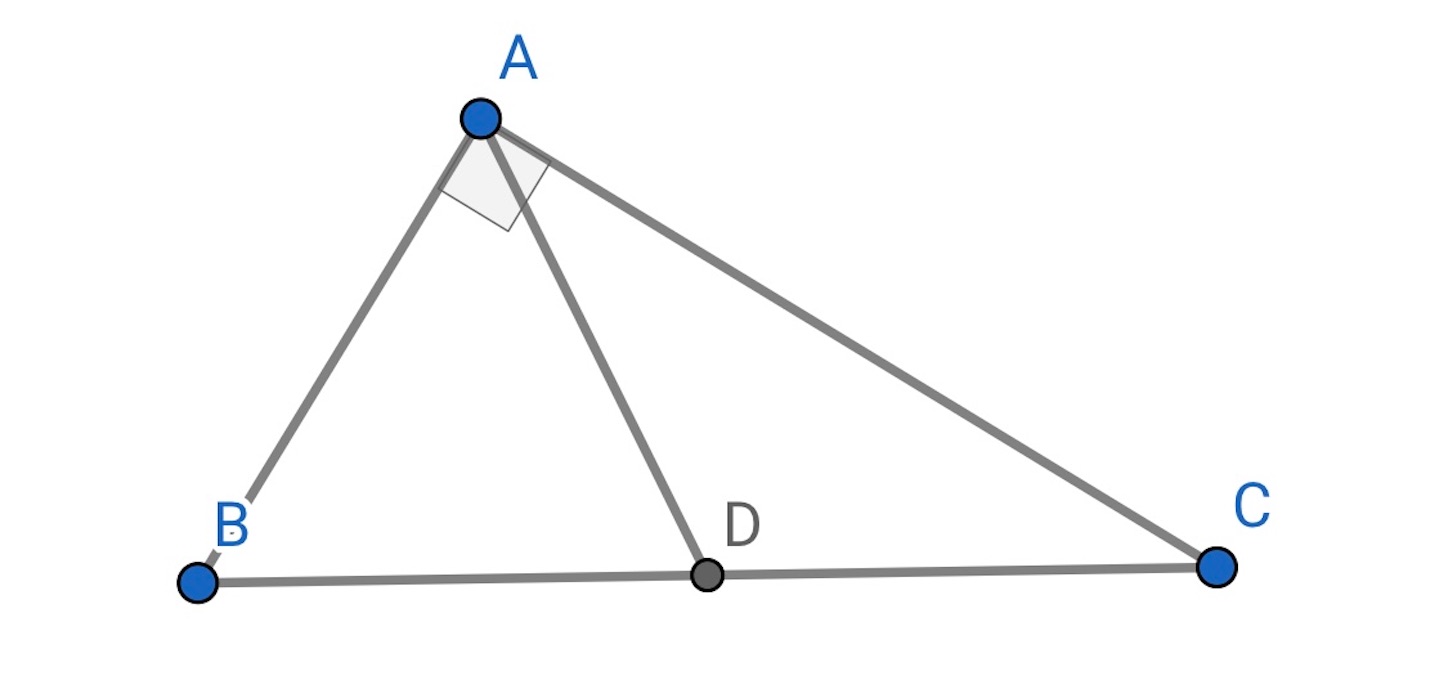
【証明】

直角三角形の斜辺である線分 $BC$ 上の点として, $\angle BAD' = \angle B$ となるように点 $D'$ をとる. $\angle B$ は鋭角だから, そのような点 $D'$ は線分 $BC$ 上にいつも存在する. $\triangle D'AB$ は二等辺三角形となるので, $AD = BD'$ である. このとき, $\angle B + \angle C = 90^\circ$ だから, $\angle D'AC = \angle C$ であり, $\triangle D'AC$ も二等辺三角形となって, $BD' = AD' = CD'$ , すなわち点 $D'$ は線分 $BC$ の中点 $D$ である.

$2$ 点を結ぶ線分の長さが $0$ のとき, その $2$ 点は同一とみなされる. 線分 $BC$ 上の任意の点において, $BX = XC$ を満たす点 $X$ が, $D$ 以外に $D_1$ もそうだとすると,

$BD + DC = BC$ ,
$BD_1 + D_1 C= BC$

から, 仮定から,

$BD = BD_1 = BC/2$

となって,

$BD_1 + D_1D = BD$ ,
$BD + DD_1 = BD_1$

のどちらであったとしても, $DD_1=0$ であり, $D= D_1$ で同一である.

したがって, 線分 $BC$ 上の点において, 中点 $D$ はただ一点存在するので, 逆も成立し, 線分 $BC$ 上の点が中点 $D$ であるならば,

$AD = BD$

である. //

※ 含意命題 $\forall x; p(x) \rightarrow q(x)$ において, 条件 $p(x)$ の真集合を $P$ , 条件 $q (x)$ の真集合を $Q$ とする. $\forall x; p(x) \rightarrow q(x)$ が真であることと, $P \subset Q$ であることは同値であった. ここで, 真集合 $Q$ の要素がひとつしかないとする. $Q$ の部分集合は空集合 $\emptyset$ と $Q$ 自身である. したがって,このとき, $P$ が空集合 $\emptyset$ でなく, かつ, $P \subset Q$ であれば $P = Q$ である. これは条件 $p (x)$ と条件 $q(x)$ が同値 (必要十分) であることを意味する. このことにもとづいた証明を「同一法」ということがある.

教科書にもある同一法の有名な例は, ピタゴラスの定理の逆証明である. ピタゴラスの定理は, 「二辺の長さがそれぞれ $a$ , $b$ の任意の三角形で, その二辺の挟角が $90^\circ$ ならば, 残りの辺の長さ $c$ は $c^2 = a^2 + b^2$ を満たす」というものである. ここで, 結論の条件 $c^2 = a^2 + b^2$ を真にする集合の要素は, 三角形の合同という同値関係が与えられている場合, ひとつの三角形しかない. なぜなら, 別の三角形が真集合に含まれると仮定し, その辺の長さが $a$ , $b$ , $c'$ だとすると, $c$ も $c'$ も結論の条件を真にするので,