大学入試問題から - ノリの悪い日記

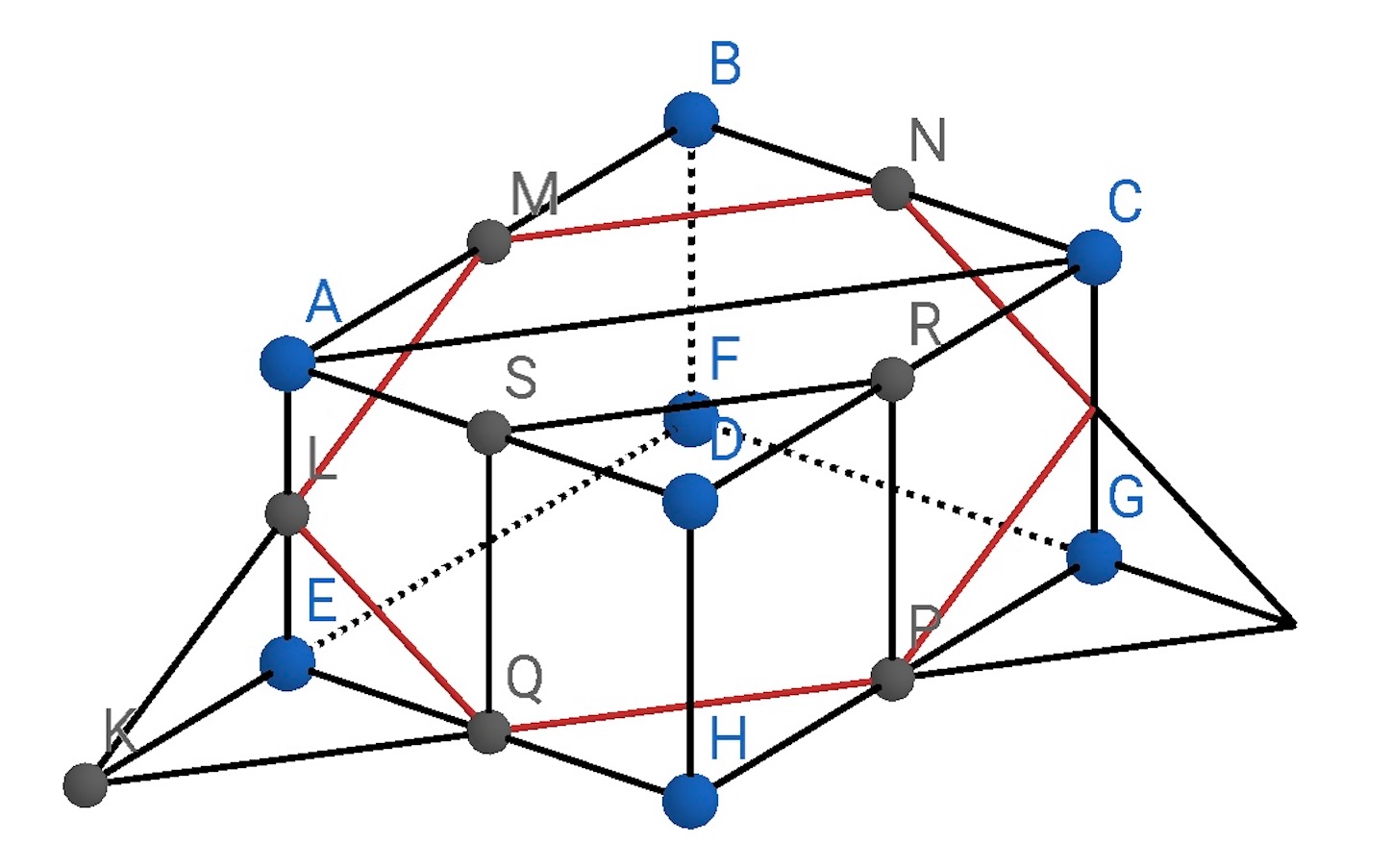
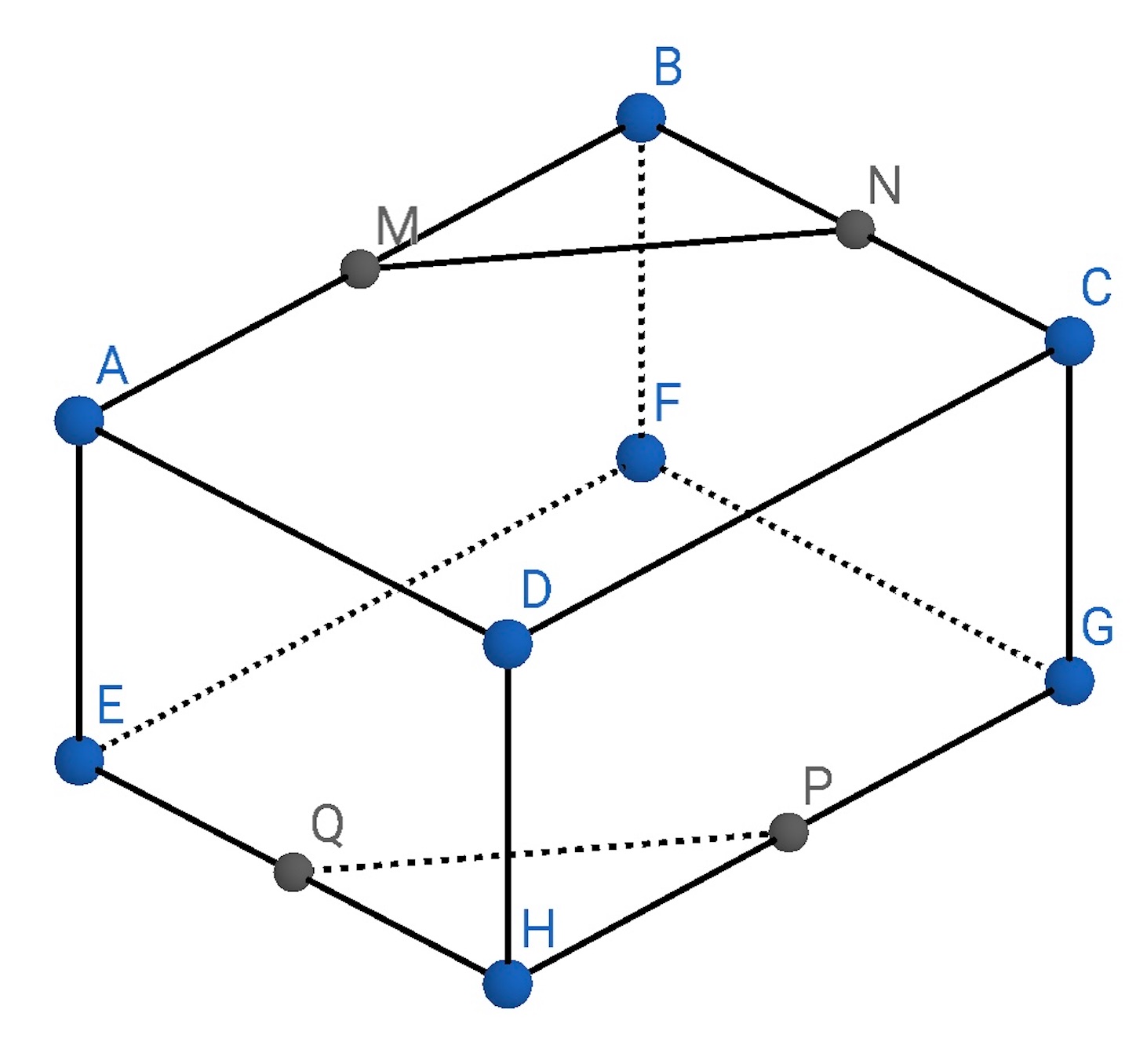
熊本大学の入試問題らしい.

【問】
図の直方体において, $4$ 辺 $AB$ , $BC$ , $GH$ , $HE$ の中点をそれぞれ $M$ , $N$ , $P$ , $Q$ とするとき, 次のことを証明せよ.

$(1)$ 線分 $MN$ , $PQ$ は同一平面上にある.

$(2)$ 上の平面と線分 $AE$ との交点は $AE$ の中点である.

【証明】
1) 辺 $AD$ , $CD$ の中点をそれぞれ $S$ , $R$ とする. 平面 $AEHD$ において, 四角形 $SQHD$ は平行四辺形 (長方形) であるから, $SQ$ と $DH$ は長さが等しく平行である. 同様にして, $DH$ と $RP$ は長さが等しく平行である.

いま, $RP$ 上の点 $X$ を任意にとり, $SQ$ と点 $X$ を含む平面 $\alpha$ を考える. $DH$ と $SQ$ (平面 $\alpha$ と平面 $AEDH$ の交線) が平行なので, $DH$ は平面 $\alpha$ に平行である. したがって, $DH$ は平面 $\alpha$ と平面 $DHGC$ の交線 (これを直線 $l$ とする) と平行である. ところが $RP$ も $DH$ と平行である. 平面幾何における「平行線の公理」は, 「定直線外の定点をすぎてこれに平行な直線はただ一つある」というものであり, $X$ から $DH$ に二本の異なる平行線が引けることはないので, $RP$ と直線 $l$ は同じである. $SQ$ と平面 $DHGC$ は平行であり, かつ $SQ$ と $RP$ がともに含まれる平面が存在するから, $SQ$ と $RP$ は平行である.

以上より, $SQ$ と $RP$ は長さが等しく平行であるから, 四角形 $SQPR$ は平行四辺形である. よって, $SR$ と $QP$ は平行である.

平面 $ADCB$ において中点連結定理により, $SR$ は $AC$ と平行, 同様にして, $AC$ は $MN$ に平行である. 平行線の公理から, $SR$ と $MN$ は平行であることがいえる (もし, $SR$ と $MN$ が交わるとすると, その交点から, $AC$ に異なる $2$ 本の平行線が引けることになって矛盾する).

以上から, $MN$ は $SR$ に平行, $SR$ は $QP$ に平行であるから, 先程とまったく同じ議論により, $MN$ と $QP$ は平行であり, 線分 $MN$ と $PQ$ は同一平面上にある (線分 $MN$ と $PQ$ を含む平面がただ一つ存在する).

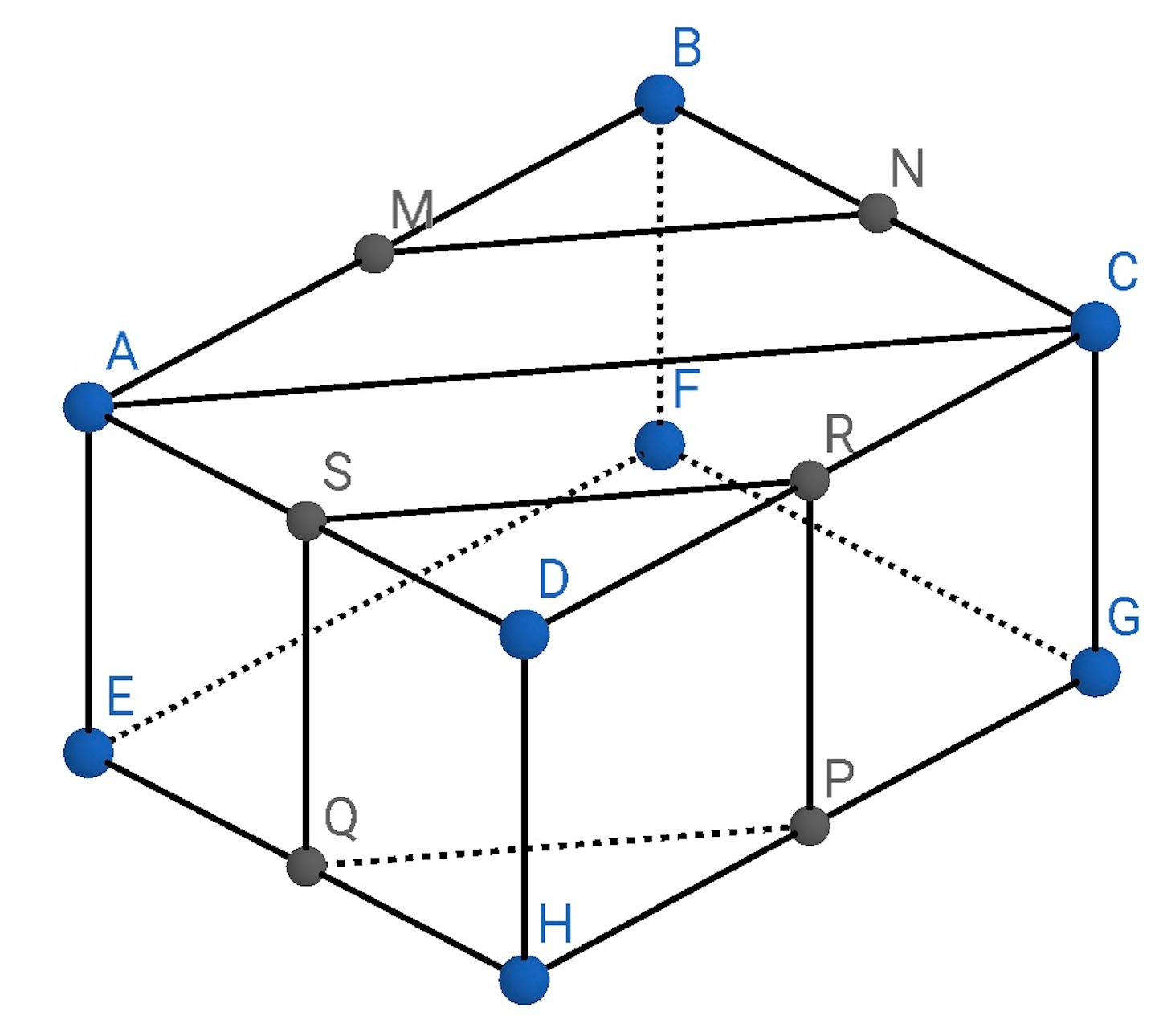
(2) 略解. 下図において, $\triangle QEK$ と $\triangle QHP$ は合同であるから, $EK = HP$ となり, このことから, $\triangle LAM$ と $\triangle LKE$ も合同であることがわかる. したがって, $AL = LE$ である.