年度の問題.
【問】
下の図のように 辺が
の立方体
があります. この立方体の対角線
上に,
となる点
をとります. このとき, 次の問に答えなさい.
と
が相似であることを証明しなさい.
線分
の長さを求めなさい.
つの点
,
,
,
を頂点とする立体の体積を求めなさい.

【解】
(1)
点 ,
,
はひとつの平面を決定する.
,
から,
は平面
に垂直である. したがって,
である. 仮設より,
である. ゆえに,
となる. は共通角で等しい.
組の角が等しいので,
と
は相似である.

(2)
だから,
答えは, である.
(3)
つ前の記事で示したのと同様にして,
は, 平面
に平行である. したがって, 三角錐
の体積は, 三角錐
の体積に等しい.
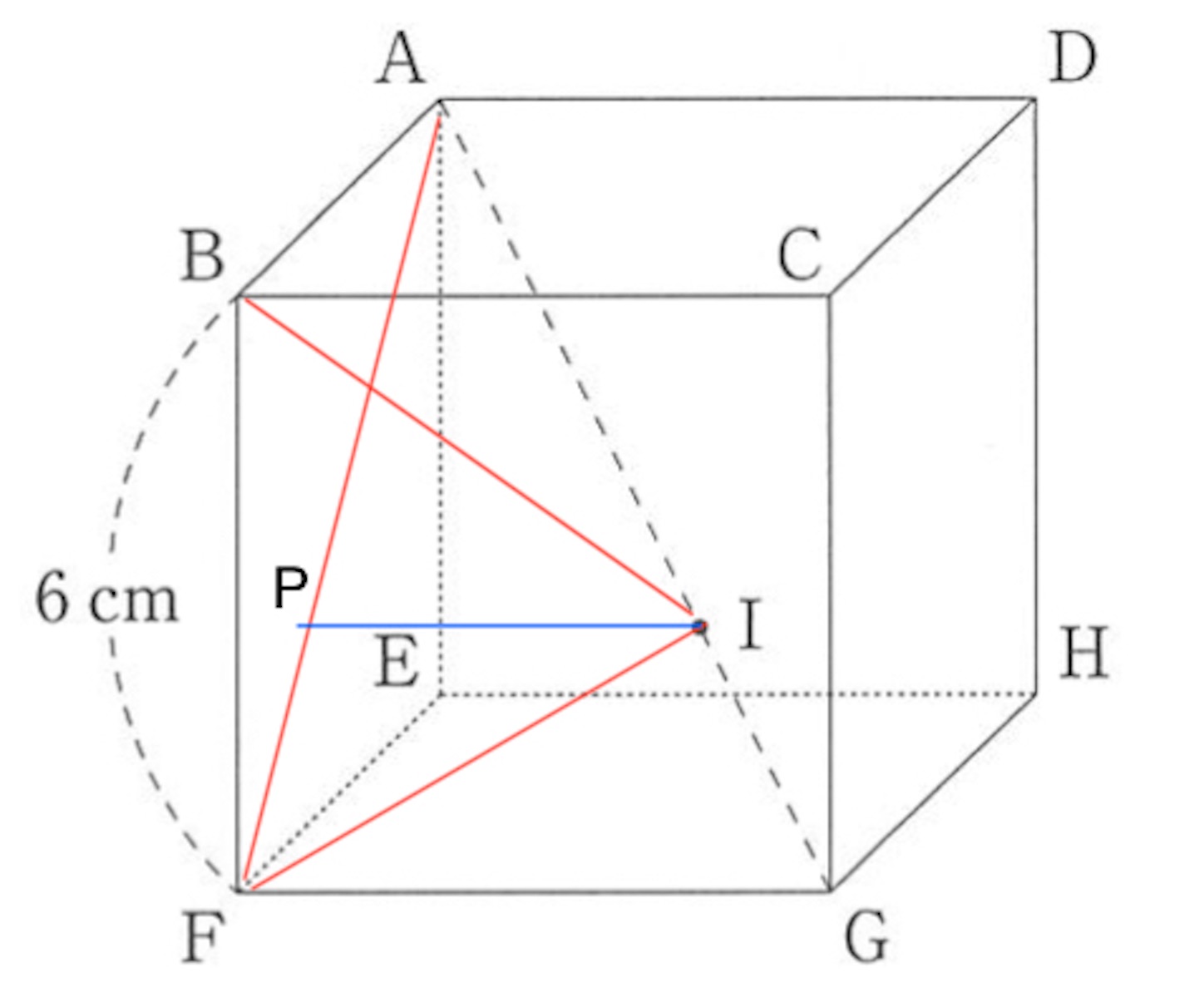
に
から下ろした垂線
の長さを求める (平面
は
を含んでいるので, 平面
に垂直である). 相似三角形の面積比から,
したがって,
だから, 求める体積は,
答えは, である. (つまり, 三角錐
の
の体積である.) //