わかる幾何学 - ノリの悪い日記

秋山武太郎の『わかる幾何學立體篇』(昭和七年) をパラパラと見ていたら, かなりの内容が, 以前感心したので紹介した昭和七年創刊の旧制中学生向けの学習雑誌の記事の内容とかぶっていることに気がついた. あの記事の内容は, 『わかる幾何學立體篇』がベースにあるダイジェストなのだ. 道理で素晴らしいはずである. 秋山武太郎のことは, いろいろな人が書いているが, 湯川秀樹も『旅人』にこう書いている. ただ, ここに書いてある「わかる幾何学」は, 平面幾何の方だとは思うが内容は未見である.

幾何学によって、私は考えることの喜びを教えられたのである。何時間かかっても解けないような問題に出会うと、ファイトがわいてくる。夢中になる。夕食に呼ばれても、母の声は耳に入らない。苦心惨憺の後に、問題を解くヒントがわかった時の喜びは、私に生きがいを感じさせた。　
幾何の教科書に出ている問題は、どんどん先の方まで解いてしまった。いろいろな参考書や問題集を買ってきて、片っぱしから解いて行った。秋山武太郎という人の「わかる幾何学」という本が、そのころ出版された。西洋の数学者に関するエピソードが、チョッピリ入っていた。この本が一番面白かった。

もう一つ気がついたのは, 二直線の位置関係である「ねじれ」という用語を昭和初期のこの当時は一切使っていないことである. 秋山先生は単に, 「同一平面中にない二直線」または「交わらずかつ平行でもない二直線」と呼んでいる. 以前紹介した学習雑誌の記事もそう呼んでいる. 「ねじれ」というのは英語の “skew” の訳らしいが, いったいいつから使われ始めたのだろう. まあ, 「同一平面中にない二直線」は, 「どんな平面も両方を含めない二直線」だとは思う. 空間の $2$ 直線の位置関係の命題は全称命題なのか存在命題なのか読んでもわからないことがある.

ところで, すでに書いてきたように, 「平面と平面が垂直」という情報をもっと活用すると少なくとも高校入試問題レベルの解答が大幅に簡単になることが多い. ただし次のことだけは知っておく必要がある. (もちろん, 秋山先生の著作には証明まで含めて詳しく書いてある.)

定理: 平面 $P$ の垂線を平面 $Q$ が含んでいるならば, 平面 $P$ と平面 $Q$ は垂直である.

平面 $P$ と平面 $Q$ が垂直のとき, 平面 $P (Q)$ 上の点から平面 $Q (P)$ に垂線を下ろすには, その点から, 平面 $P$ と平面 $Q$ の交線に垂線を下ろせばよい.

たとえば, これを使ってずっと前に解いた東京都立高校 $2017$ 年入試問題を解いてみる.

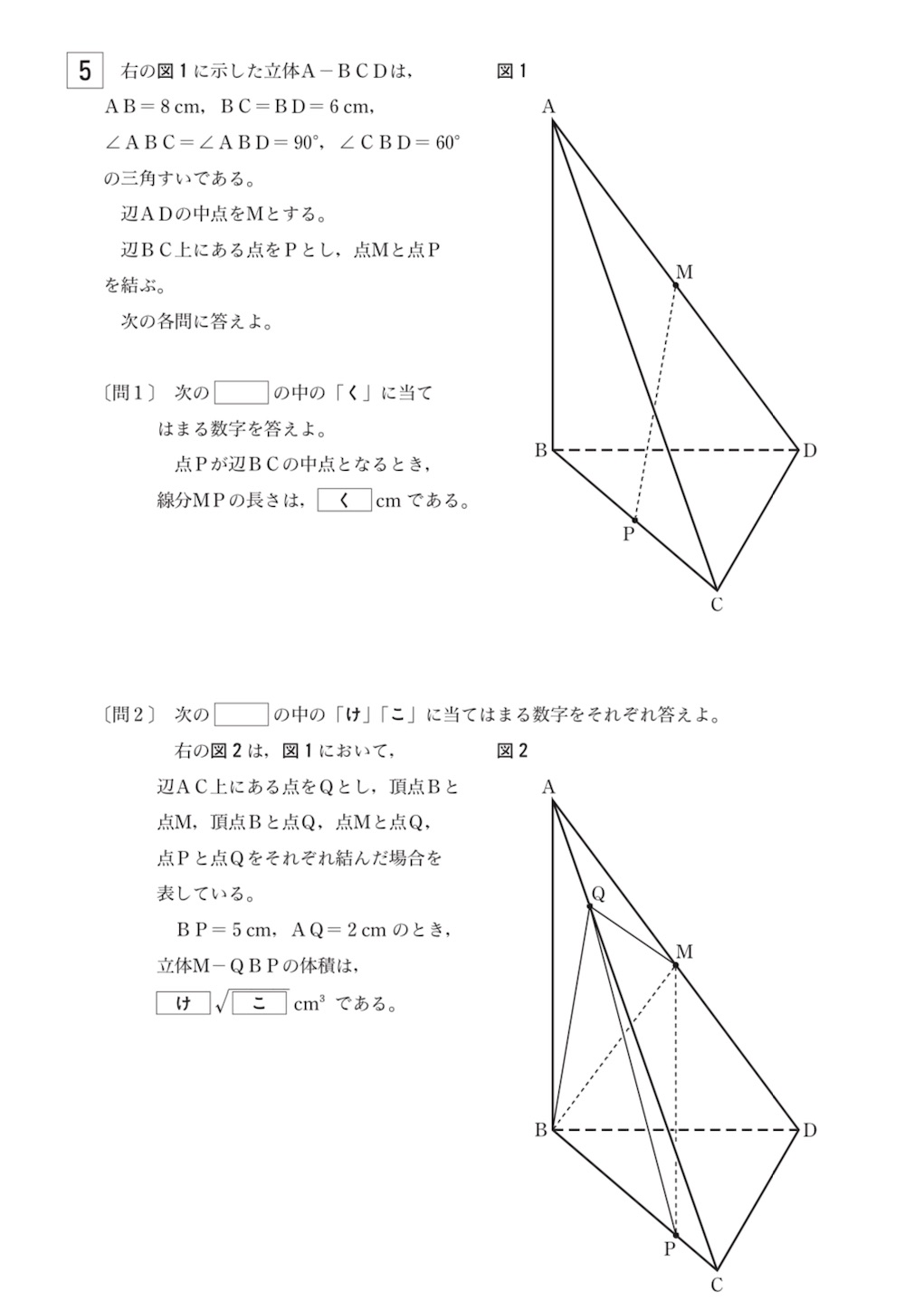
問題の条件から, $AB$ は平面 $BCD$ に垂直である. したがって, $AB$ を含む平面 $ABC$ も平面 $ABD$ も平面 $BCD$ に垂直である.

問 $(1)$

$M$ から平面 $ABD$ と平面 $BCD$ の交線 $BD$ に垂線 $MQ$ を下ろせば, $MQ$ は平面 $BCD$ に垂直だから, $\angle MQP = 90^\circ$ である. $AB$ と $MQ$ は平行だから中点連結定理より $MQ = 4$ , $Q$ は $BD$ の中点なので, $PQ = 3$ である. したがって,

$MP = \sqrt{4^2 + 3^2} = 5$

問 $(2)$

問(1) の図をそのまま流用する ( $P$ は前問のままの位置).

$D$ から $BC$ に垂線 $DP$ を下ろせば, $DP$ は平面 $ABC$ への垂線である. 平面 $APD$ は, $DP$ を含むから, 平面 $ABC$ と平面 $APD$ は垂直である. したがって, $M$ から, $AP$ に垂線 $MR$ を下ろせば, $MR$ は, 平面 $ABC$ に垂直である. $MR$ と $DP$ は平行なので, 中点連結定理により,