ノリの悪い日記

古今東西の映画、ポピュラー音楽、その他をいまここに交錯させながら随想します。

別解?

立体幾何初歩 中学数学

ネットを見ていたら, 下図において, 側面がすべて長方形の三角柱で, AB = 5, BC =3 , AD =6 , \angle{ABC} = 90^\circ のとき, 点 A から, 平面 CDE に下ろした垂線の長さを求めよという問題があった.

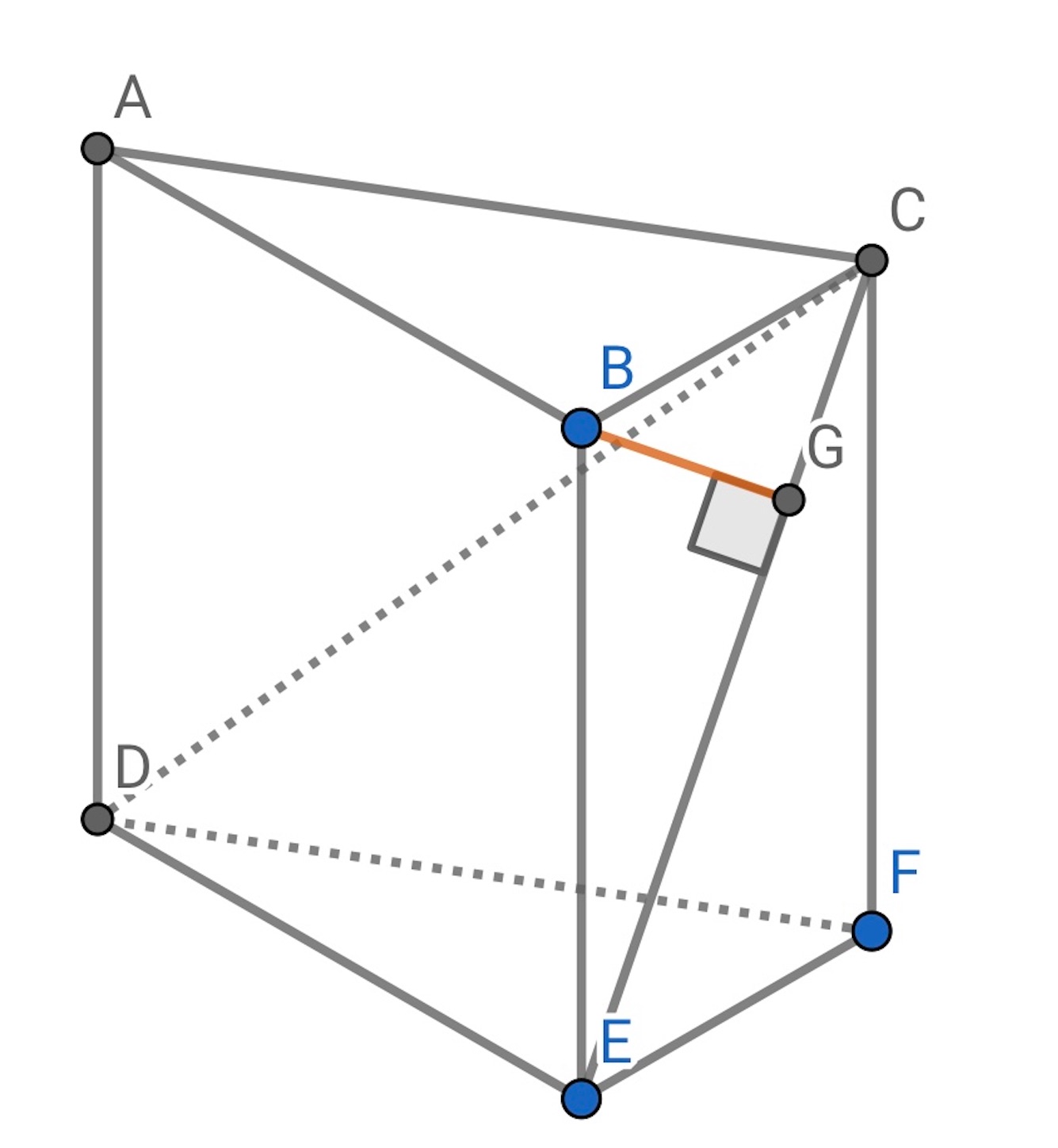
普通に三角錐の体積から求めれば良いのだが, 別解といわれる方法がどうもしっくりこないので, じゃあ自分だったらどう解くのか考えてみた.

まず, DE は BE とも EF とも垂直なので, DE は, 平面 BEFC に垂直である. 平面 CDE は, DE を含むので, 平面 BEFC と平面 CDE は垂直である. 二つの平面の交線は CE であり, したがって, B から平面 CDE に下ろした垂線の長さは, 交線 CE に下ろした垂線 BG の長さである.

ところで直線 AB は平面 ADEB に含まれているが, 平面 ADEB と平面 CDE の交線は, 直線 DE である. 直線 AB と直線 DE は平行である. つまり, 直線 AB は平面 CDE と共有点を持たないので, 直線 AB と平面 CDE は平行である. したがって, 点 A から平面 CDE に下ろした垂線の長さは, BG の長さに等しい.

EC = \sqrt{3^2 + 6^2} = 3\sqrt{5}
\triangle BCE = 9

だから,

\displaystyle{BG = \frac{6}{\sqrt{5}} = \frac{6}{5} \sqrt{5} }

で, 点 A から平面 CDE に下ろした垂線の長さは

\displaystyle{\frac{6}{5} \sqrt{5} }

である.
//