ノリの悪い日記

古今東西の映画、ポピュラー音楽、その他をいまここに交錯させながら随想します。

雑記 (2)

初等幾何 中学数学

ネットで見かけた問題をただやってみた. どこかの高校入試の問題だと思う.

問題の要旨は一辺の長さが 4 の正方形 ABCD で, 辺 AB 上に点 E を BE = 1, 辺 BC 上に点 F を BF= 3 になるようにとって、図のようにするとき、 \triangle GEF と \triangle GBF の面積比を求めよというものである。

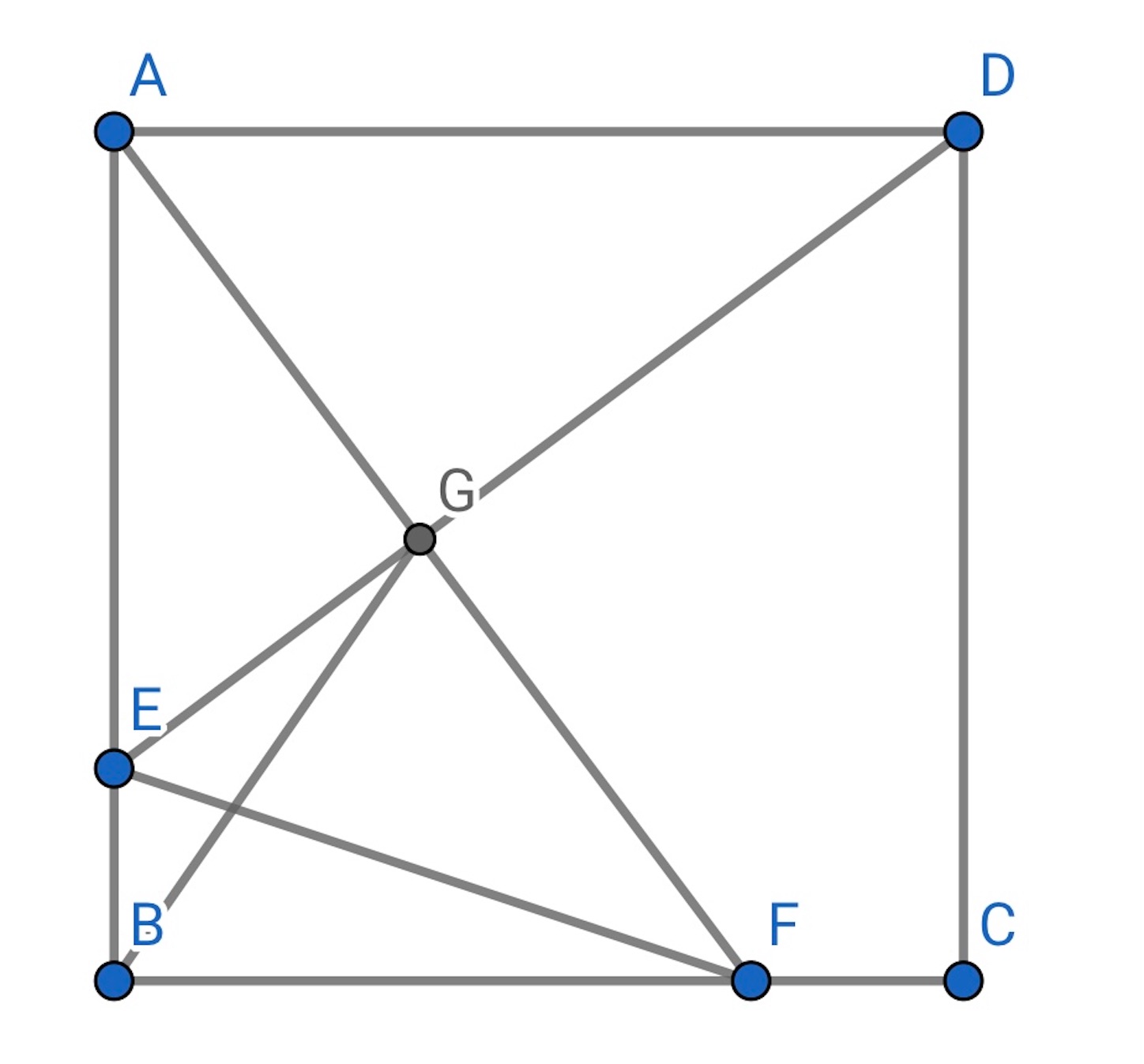
(解)

四角形 EBFG の頂点は同一円周上にある。まず、相似から、

\displaystyle{EG=\frac{9}{5}},
\displaystyle{GF=5-\frac{12}{5}=\frac{13}{5}}

である。補角をなす場合の面積比を考えれば、

\displaystyle{ \triangle EBG: \triangle GBF \\ =1 \times \frac{9}{5}: \frac{13}{5} \times 3 \\ = 3:13 }

\displaystyle{ \triangle GEF: \triangle BEF \\ = \frac{9}{5} \times \frac{13}{5} : 1 \times 3 \\ = 39:25 }

したがって、

\displaystyle{ \triangle GEF: \triangle GBF \\ = \frac{39}{64}: \frac{13}{16}\\ = 3:4 }

である。//

※ こんなことをしなくても、もっと簡単なのは、 B から AF に垂線を下ろしてその足 (点 H とする) との距離を相似で求めると、

EG: BH = 3:4

だから、底辺共通より

\displaystyle{ \triangle GEF: \triangle GBF = 3:4 }

である。