雑記 - ノリの悪い日記

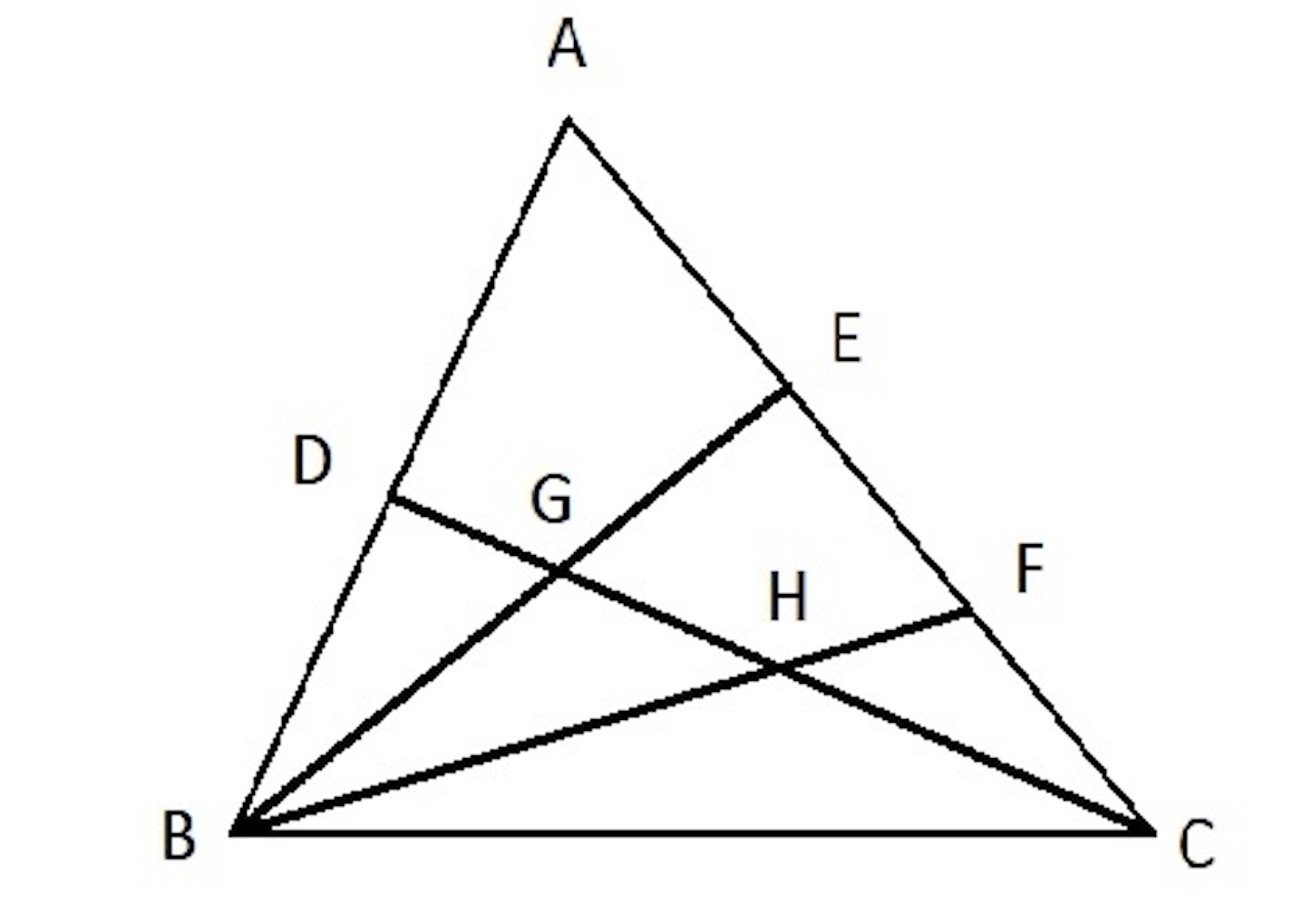
前に紹介した、神奈川県公立高校の2019年入試問題で、解き方はいろいろあるのだが、面積比を使って長さの比を求めるやり方は意外と簡単だなあと最近思ったので、ちょっと記事にしておく。この問題は実際の入試で正答率 2 % 台だったのである。

【問】
三角形 $ABC$ があり、辺 $AB$ の中点を $D$ とする。また辺 $AC$ を三等分した点のうち、点 $A$ に近い点を $E$ , 点 $C$ に近い点を $F$ とする。さらに線分 $CD$ と線分 $BE$ の交点を $G$ , 線分 $CD$ と線分 $BF$ の交点を $H$ とする。三角形 $BGD$ の面積を $S$ , 四角形 $EGHF$ の面積を $T$ とするとき、 $S$ と $T$ の比を最も簡単な整数の比で表しなさい。

(解)

$\displaystyle{ BG:GE=\triangle DBC: \triangle EDC}$ ,
$\displaystyle{ BH:HF=\triangle DBC: \triangle FDC}$

である。三角形 $ABC$ の面積を $1$ とおけば、

$\displaystyle{\triangle DBC=\frac{1}{2}}$
$\displaystyle{\triangle EDC=\frac{1}{2} \times \frac{2}{3}}$
$\displaystyle{\triangle FDC=\frac{1}{2} \times \frac{1}{3}}$