陥没地帯 (295) - ノリの悪い日記

シムソンの定理の初等幾何による証明が出てきたのでスタイネル (Steiner) の定理の初等幾何による証明もみておく.

【定理】

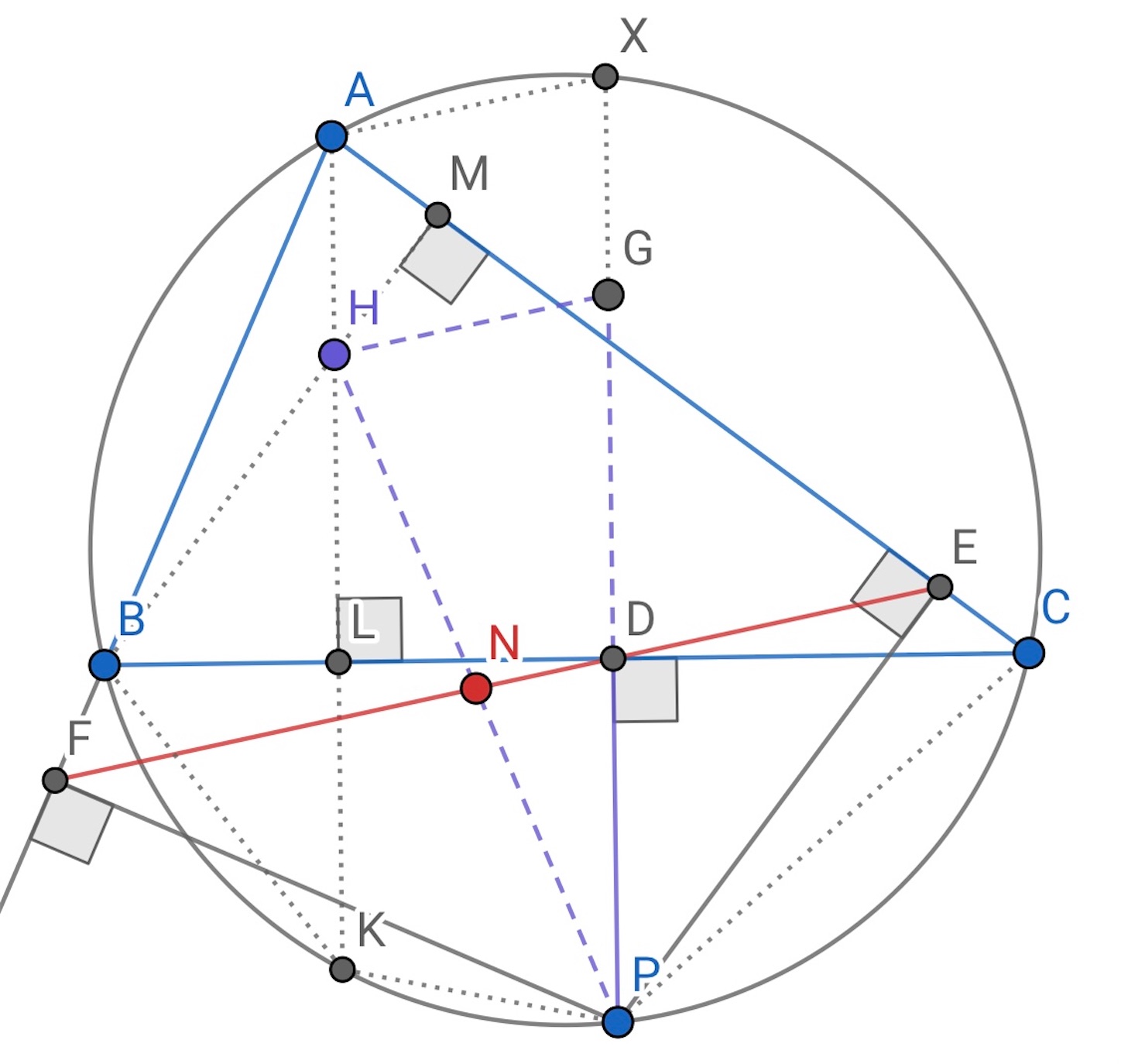
$\triangle ABC$ の垂心を $H$ とし, 外接円周上の $1$ 点を $P$ とすると, 点 $P$ の $\triangle ABC$ に関するシムソン線は線分 $PH$ の中点を通る.

f:id:noriharu-katakura:20211201232253j:plain

【証明】

最初に記号の定義をする.

シムソン線上の点 $D$ , $E$ , $F$ をそれぞれ, $P$ から $BC$ , $CA$ , $AB$ に下ろした垂線の足とする.

$PH$ の中点を $N$ とする.

$A$ から $BC$ に下ろした垂線の足を $L$ とし, $AL$ が再び外接円と交わる点を $K$ とする. また, $B$ から $CA$ に下ろした垂線の足を $M$ とする.

$BC$ を対称軸として $P$ の対称点を $G$ とし, 直線 $PDG$ が再び外接円と交わる点を $X$ とする.

次に証明の方針であるが,

$ND$ は $\triangle PGH$ の辺 $PG$ の中点と, $PH$ の中点を結んだ線であるから, 中点連結定理により, $ND$ と $HG$ は平行である. したがって, $HG$ と $DE$ が平行であることが証明できれば, $N$ はシムソン線 $FDE$ 上にあるといえる.

$HG$ と $DE$ が平行であることの証明:

$\angle GDE = \angle HGD$ であることを示すことによって証明する.

まず, $\angle PDC = \angle PEC = 90^{\circ}$ なので, 点 $D$ , $P$ , $C$ , $E$ は同一円周上にある。

したがって, $\angle GDE = \angle ACP$ であるが, $\angle ACP = \angle AXP$ なので, $\angle GDE = \angle AXP$ である. $XP$ と $AK$ は平行であるから,

$\angle AXP + \angle KAX = 180^{\circ}$

である. 四角形 $AKPX$ は円に内接しているから,

$\angle KPX + \angle KAX = 180^{\circ}$

したがって,

$AXP = \angle KPX$

である. これから, $\angle KPX = \angle HGD$ がいえると, $\angle GDE = \angle HGD$ がいえ, $HG$ と $DE$ が平行であることが証明できる.

$\angle KPX = \angle HGD$ であることの証明:

$\triangle HBL$ と $\triangle HAM$ は相似だから, $\angle HBL = \angle HAM$ である. ところが, $\angle HAM = \angle KAC = \angle KBC= \angle KBL$ なので, $\angle HBL = \angle KBL$ である. したがって, $\triangle HBL$ と $\triangle KBL$ は合同であり, $LH = LK$ である. したがって, $KP$ と $HG$ は $BC$ について対称であり, このことから, $\angle KPX = \angle HGD$ であることがいえた.

以上から $HG$ と $DE$ は平行であり, したがって, $N$ はシムソン線上にある.
//