年共通テスト, 数学
から. 黄金比 (この問題では
) を使って計算を効率よくやることについては, 記事
で触れておいた.
【問】
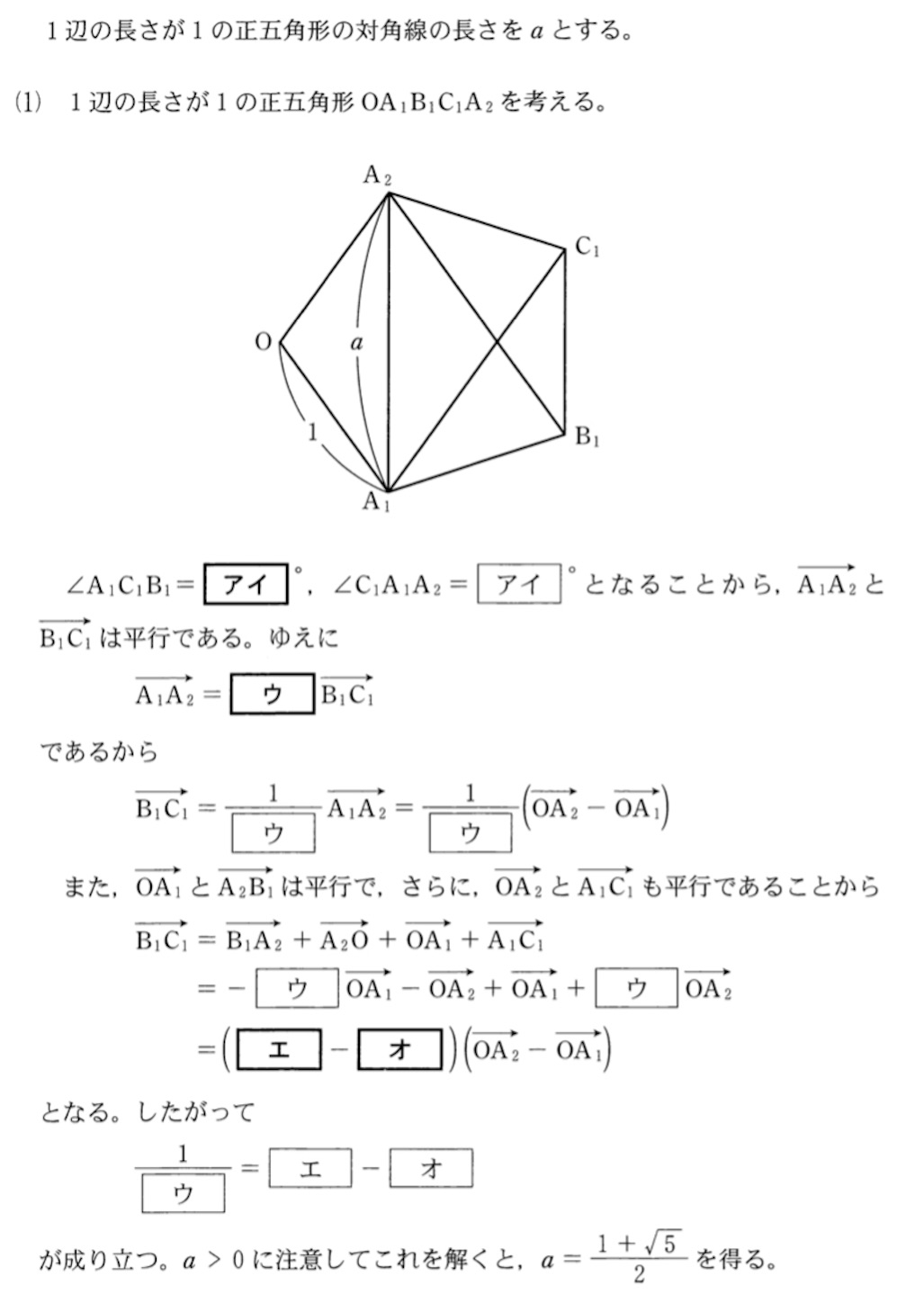
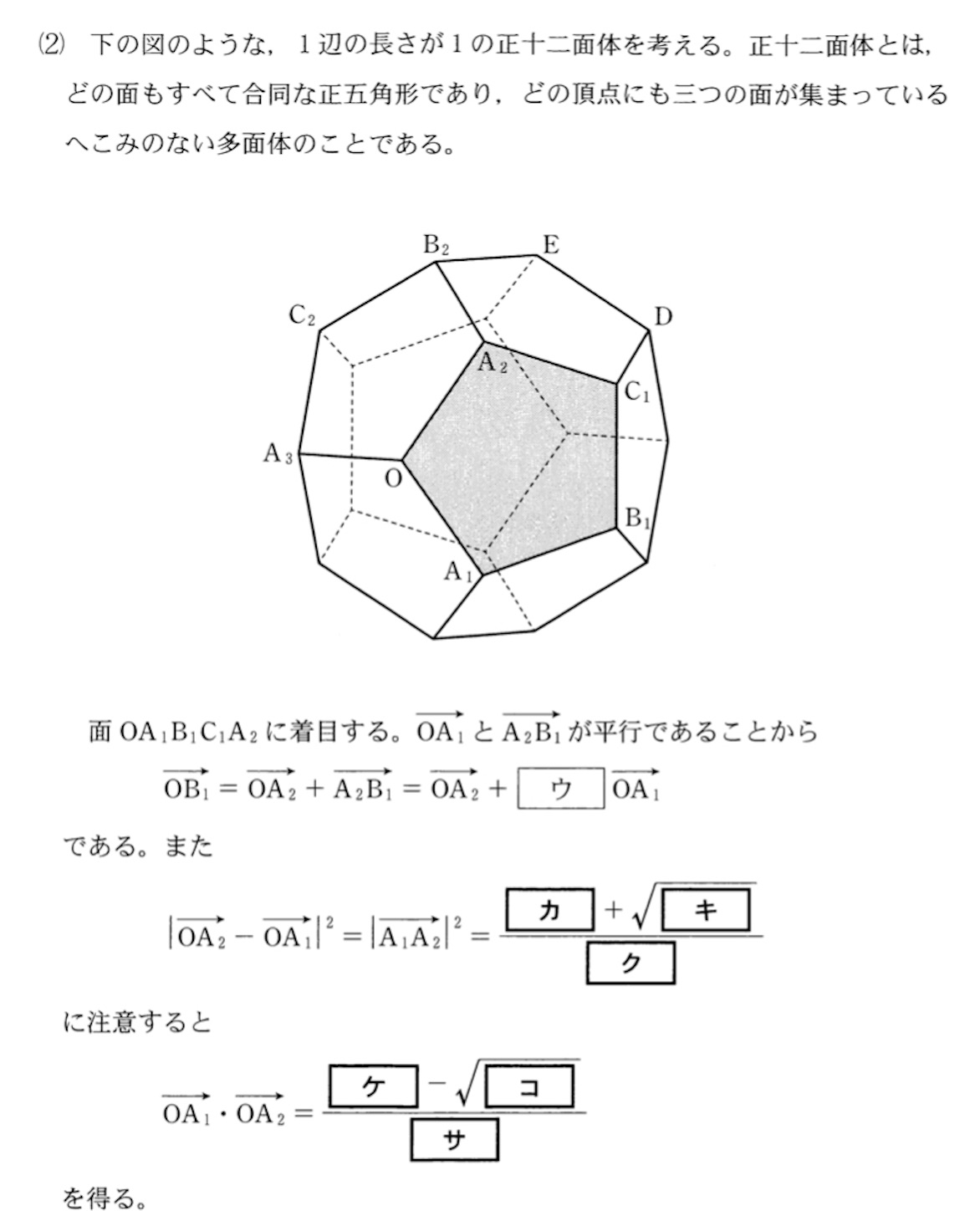
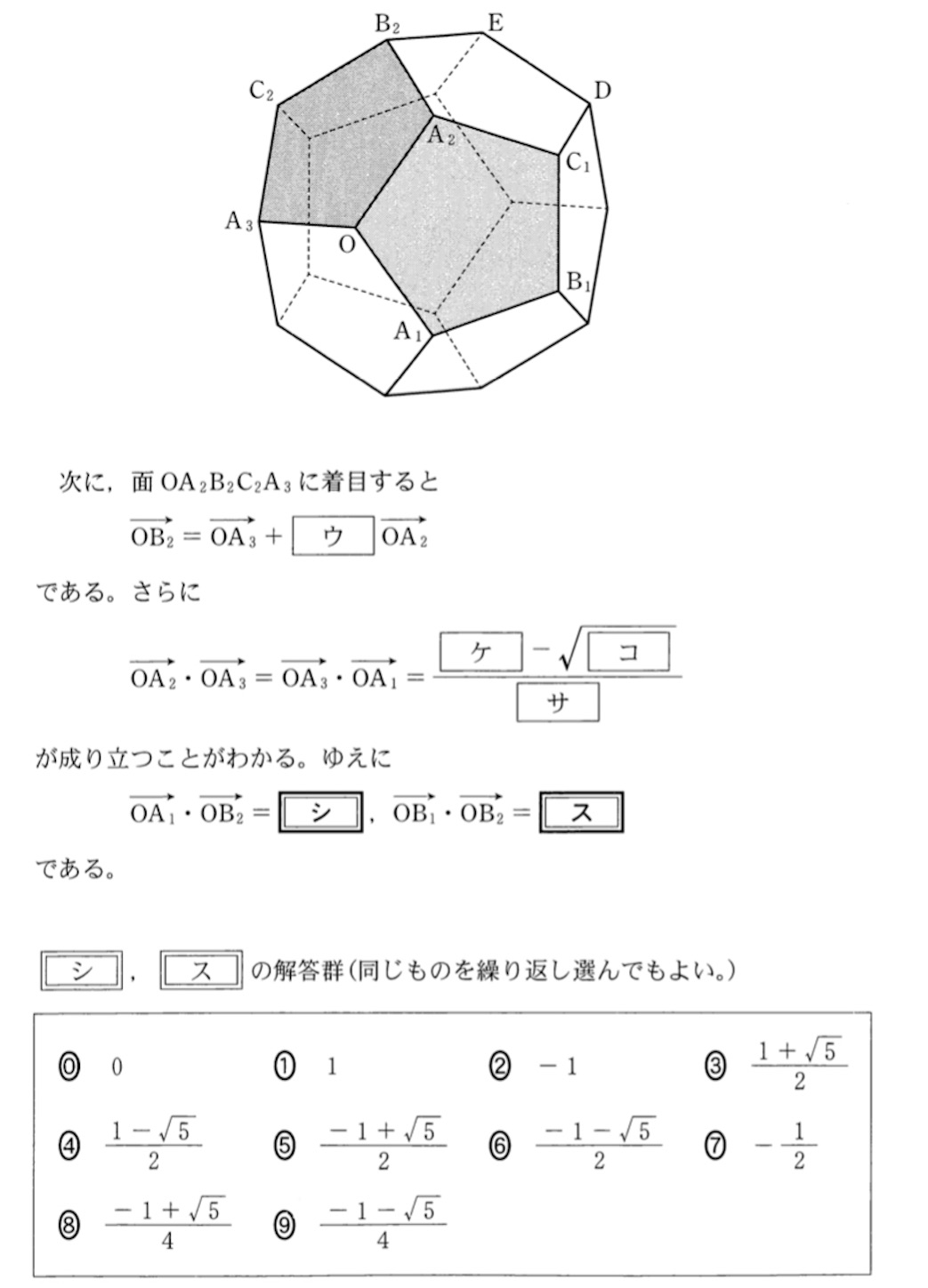
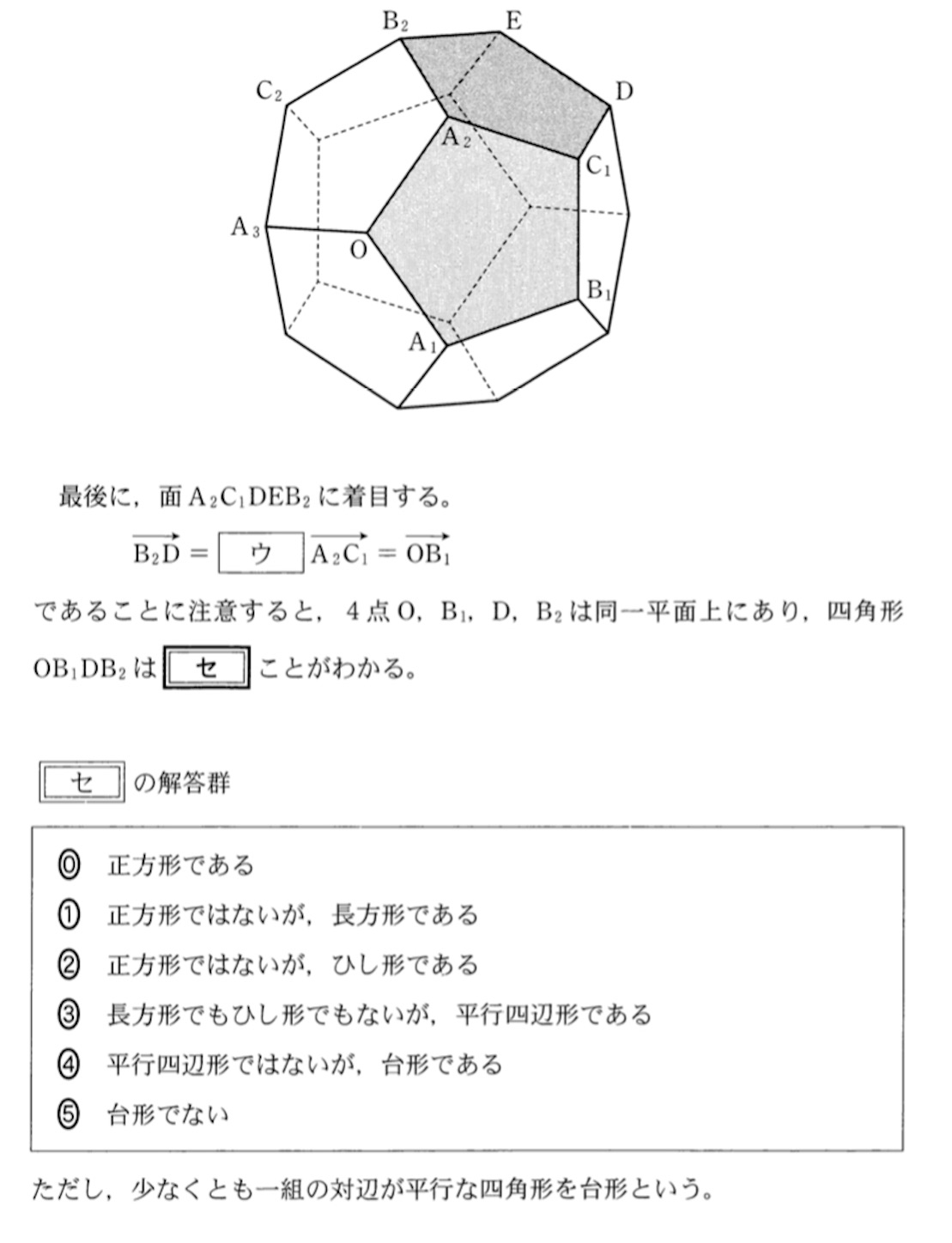
【解】
また,
したがって,
つまり,
したがって, 四角形 は正方形である.
//
年共通テスト, 数学
から. 黄金比 (この問題では
) を使って計算を効率よくやることについては, 記事
で触れておいた.
【問】




【解】
また,
したがって,
つまり,
したがって, 四角形 は正方形である.
//