ノリの悪い日記

古今東西の映画、ポピュラー音楽、その他をいまここに交錯させながら随想します。

陥没地帯 (284)

高校数学 初等幾何

センター試験の過去問題から, もう 1 問, 2013 年の図形問題をやってみることにした. 設問の中の OD の長さがわからないで, そのまま沈没した受験生が多かったとあるが, それは何かの世迷いごとで, まさかなあと思ってしまう.
※ なお, 記事 (187) には, 2017 年センター試験の図形問題がある.

【問】
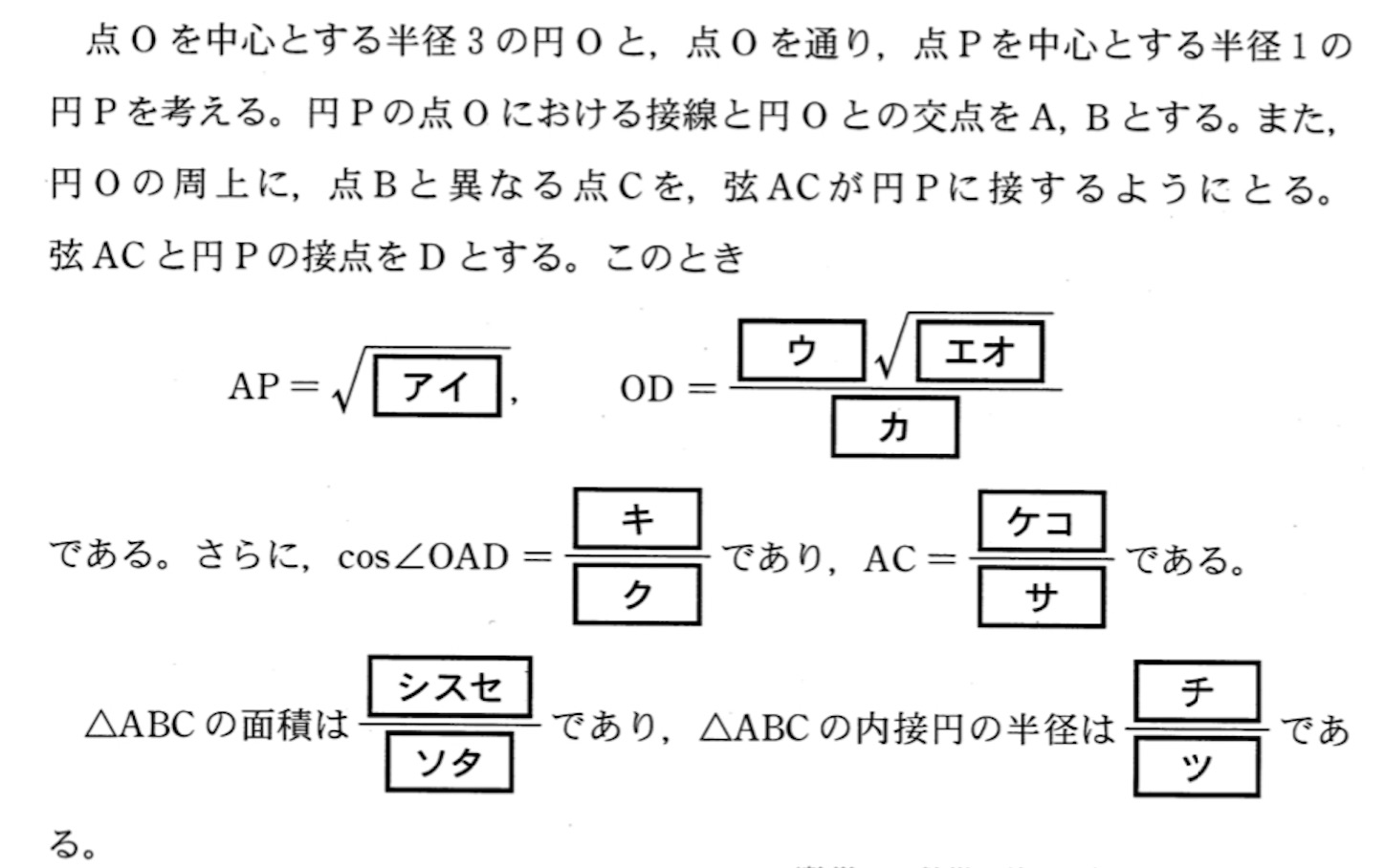
f:id:noriharu-katakura:20211121214209j:plain
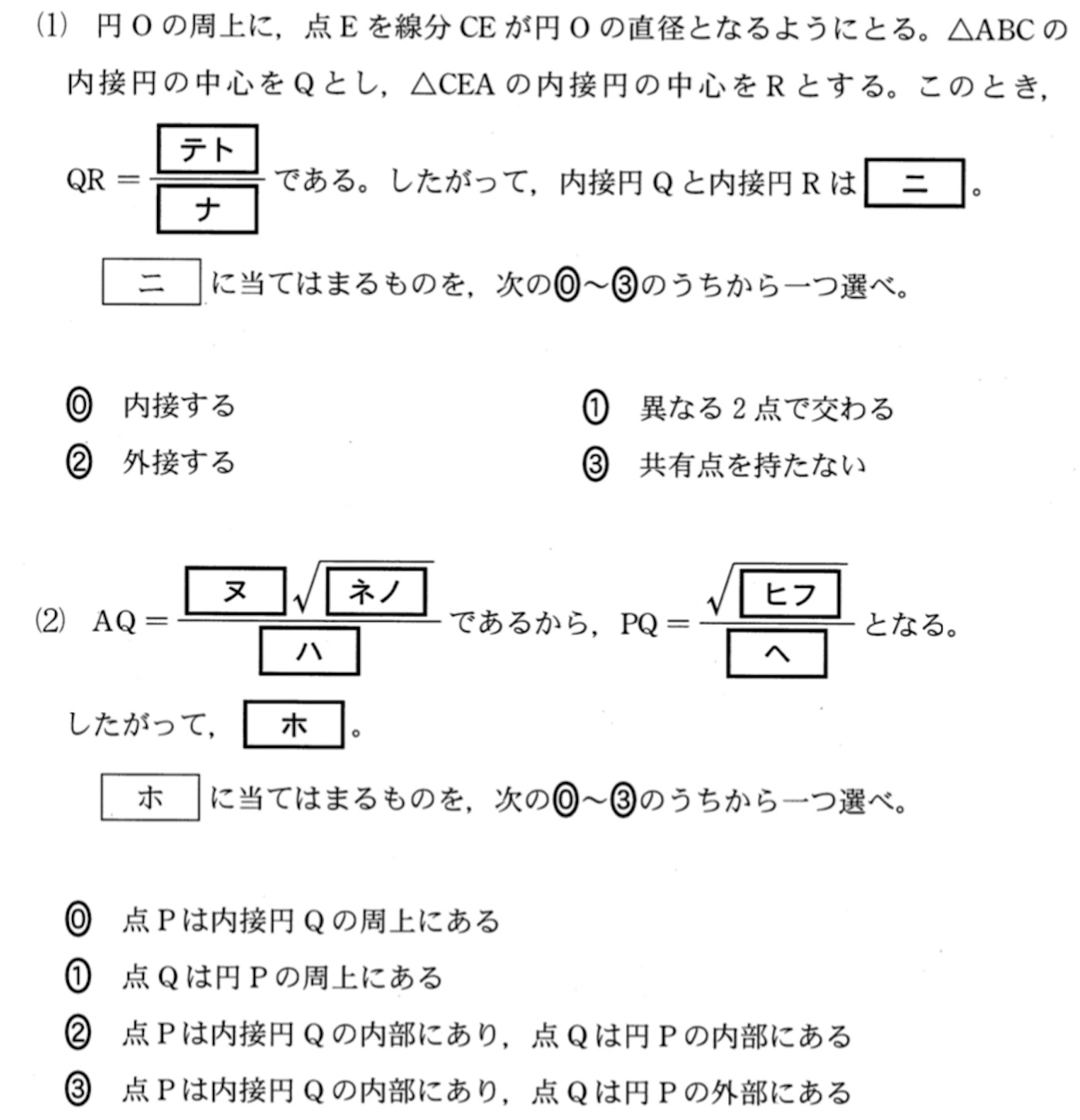
f:id:noriharu-katakura:20211121210314j:plain

【解】
AP = \sqrt{3^2 + 1^2} = \sqrt{10}

点 O, A, D, P は同一円周上にあるので, トレミーの定理から,

\sqrt{10}\cdot OD = 1 \cdot 3 + 1 \cdot 3
\displaystyle{OD = \frac{3\sqrt{10}}{5}}

※ 対角線 OD , AP は直交していることから, 直角三角形の相似を使って OD を求めることや, 下の三角関数から求めることは, 別解としてすぐに思いつく. //

\angle PAD = \angle PAO = \theta とおくと, \angle OAD = 2\theta であり,

\displaystyle \sin \theta = \frac{1}{\sqrt{10}}, \displaystyle \cos \theta = \frac{3}{\sqrt{10}}

から,

\displaystyle{ \cos 2\theta = 1-2\sin^2 \theta = \frac{4}{5}}
\displaystyle{ \sin 2\theta = 2\sin \theta \cos \theta = \frac{3}{5}}

\displaystyle{AC =BA\cos 2\theta = \frac{24}{5}}
\displaystyle{BC =BA\sin 2\theta = \frac{18}{5}}

\displaystyle{ \triangle ABC = \frac{1}{2}\cdot \frac{24}{5} \cdot \frac{18}{5} = \frac{216}{25}}

\displaystyle{s = \frac{1}{2}\left(6+ \frac{24}{5} + \frac{18}{5}\right) = \frac{36}{5}}

内接円の半径 r は,

sr = \triangle ABC から,

\displaystyle{ r = \frac{216}{25} \cdot \frac{5}{36}= \frac{6}{5}}

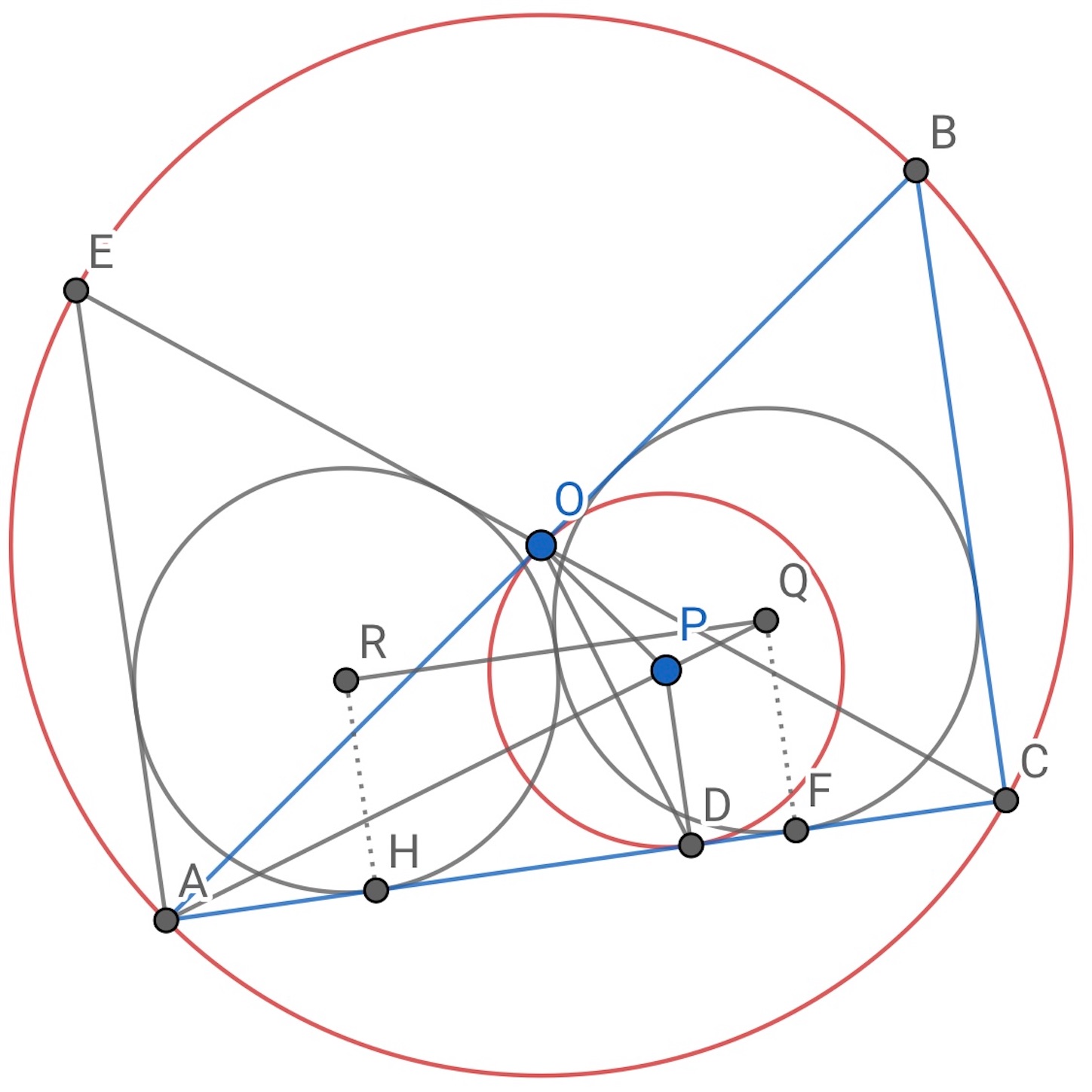
f:id:noriharu-katakura:20211122003825j:plain

(1)
QR = FH = AC - AH- CF

ここで,

\displaystyle{CF = AH = \frac{6}{5} }

なので,

\begin{align} QR= \frac{24}{5} -2 \cdot \frac{6}{5} = \frac{12}{5} \end{align}

したがって, 円 Q と円 R は互いに外接している.

(2)
A, P, Q は同一直線上にある.

AQ \cdot \sin \theta = r だから,

\displaystyle{ AQ = \frac{6\sqrt{10}}{5} }

\displaystyle{PQ = AQ - AP = \frac{\sqrt{10}}{5} }

したがって, 点 P は円 Q の内部にあり, 点 Q は円 P の内部にある.
//