散歩していたら, 菊の展示をやっていたので, ちょっと覗いたら, 肥後菊があった. 伊勢菊もあったけれど, 花の状態は少しよくなかった.


年, センター試験の数学
は平均点が例年の中でもっとも低いので, 難易度が高いとされる問題をやってみた. 最初の問は図形の問題だが, はっきり言って, どこが難しいのかなあ. ただ基本公式を当てはめていくだけで容易に解けるし, 公立高校入試の図形問題の方がよほど難しいものが出題されている気がする. たしかに作図は上手く描かないとちょっとゴチャゴチャはしてくるけれど…… もう
つの問は, 場合の数と確率の問題で, これは, 確率において場合の数をどう数えるかという基本がしっかり理解されていないと, 最初から間違ってしまう恐れがあり, そういった意味では, 以降のほとんどの問を落としてしまう可能性があるという点で, 怖い問題であるといえるだろう.
【問 】

【解】
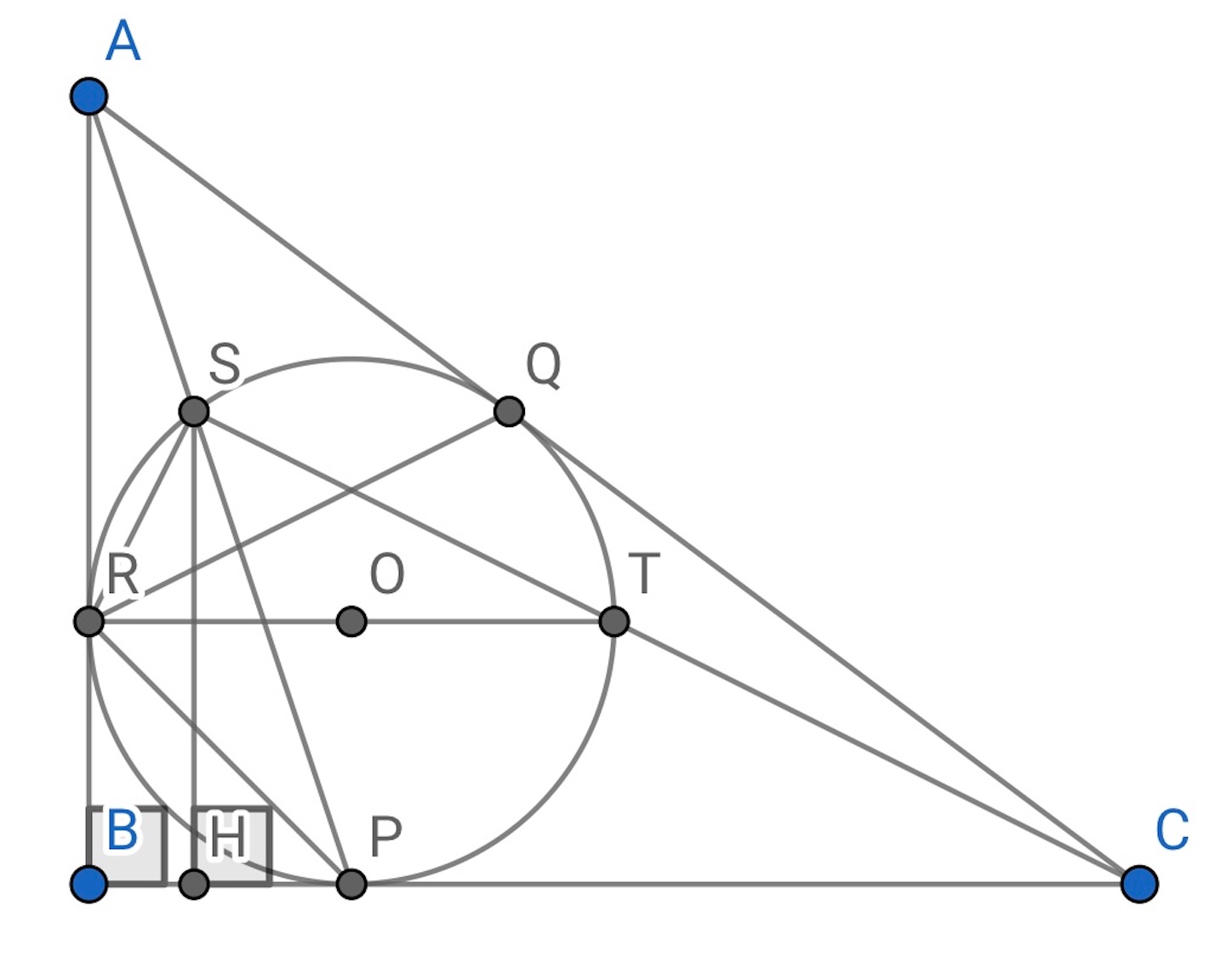
とする *1.
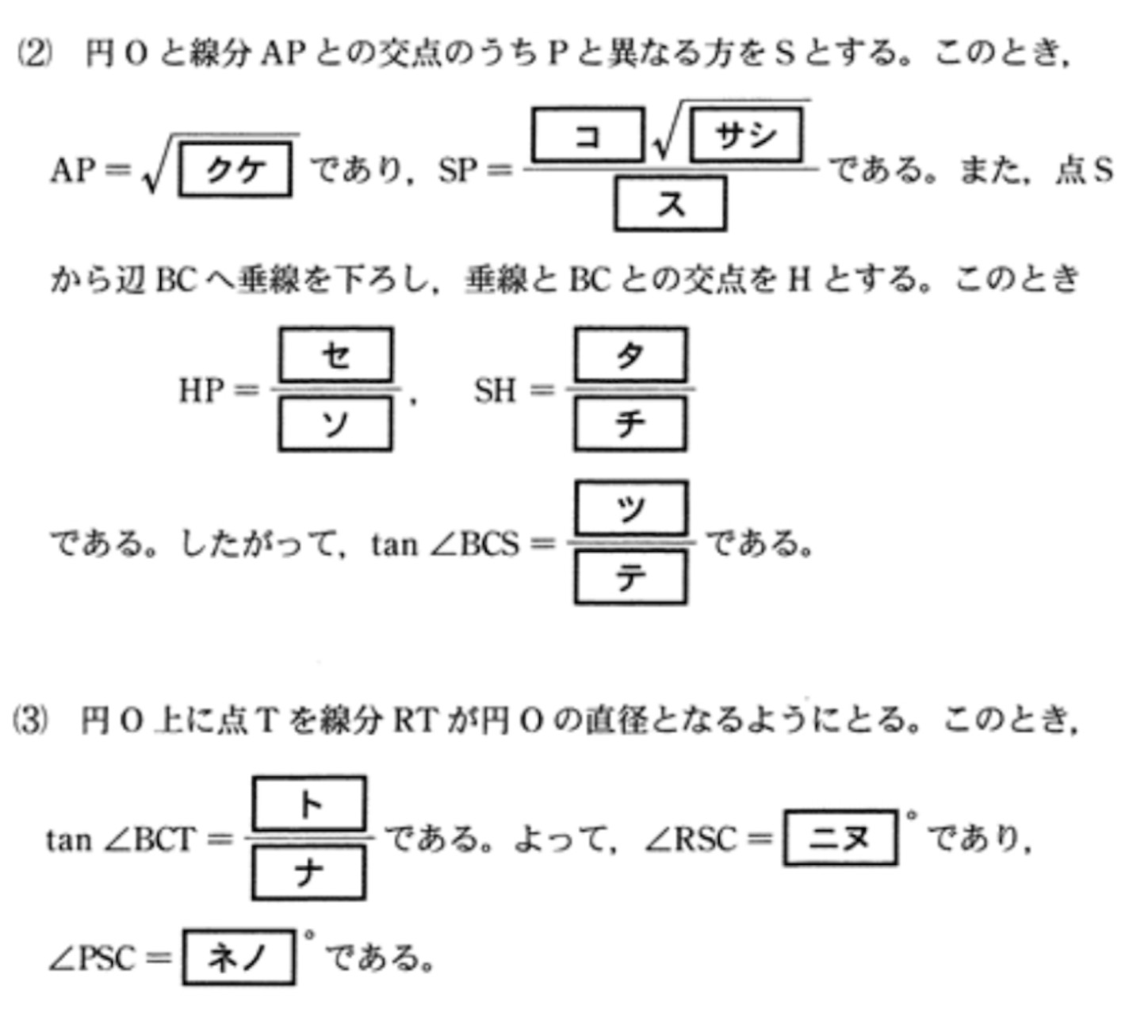
内接円の半径を
とすれば,
だから,
となる.
だから, 余弦定理により,
したがって,
である. また, 正弦定理より,
となって,
である.
なので, ピタゴラスの定理から,
である. 方べきの定理から,
これから,
三角形の相似より,
したがって,
であるから,
であることは, から,
に垂線を下ろせばすぐわかる. このことから,
は, 線分
上の点であることがわかった. したがって,
である. また, 円周角から,
である.
//
【問 】

【解】
ある意味, 最初の問に即答できるかが一番重要なことであると思う. この場合, すべての玉を区別して考えるので, 最初の問は, 個の区別された球から
個を取り出す (取り出しただけで玉は並べない) 場合の数を訊いているのだから, 単に組合せを計算すればよいのである. なお, 赤と白の玉は, (番号, 色) で識別されている.
※ ここでの「玉」は, 写像 相でいえば, 区別された
個の箱に, 5 個の区別されないボールをたかだか
個入れる問題であることに注意する. 問題の「玉」が, モデルの方では「箱」に対応しているのがややこしい. 具体的なモノに喩えたモデルは分かりやすいが, しばしば適用の際に混乱する元になる. *2 また, 後の問題の数え上げではその都度, 異なるモデルで考えなければならない. //
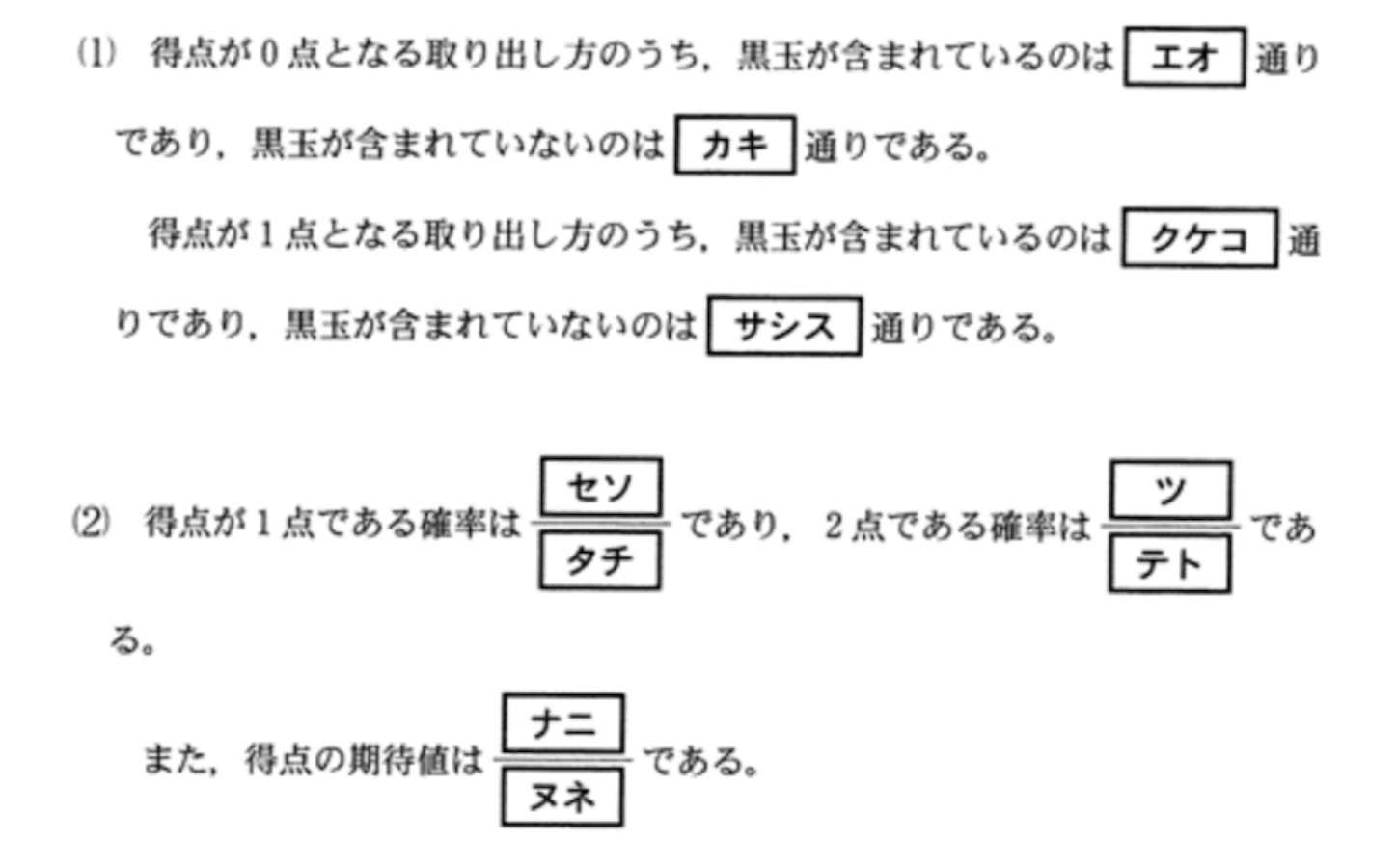
得点が
となる組合せ方は, まず, 黒玉が含まれている場合, 残り
個の玉の番号はすべて異なっていなければならず, また選択した番号それぞれに, 赤と白の玉のどちらかを割り当てるので,
通りである.
※ 今度は, から
番まで番号のついた区別されたボールから,
個を選択し, 赤と白の箱のどちらかへ投げ入れるモデルで数えている. //
また, 黒玉が含まれていない場合は, 個の玉の番号はすべて異なっていなければならず, それぞれの番号に, 赤と白のどちらかを割り当てるので, 組合せ方は,
通りである.
同様に, 得点が 点の場合は, まず, 黒玉が含まれていると, まず
から
までの数から
つを選択し (赤, 白両方を対応させ), 残る
つの番号から
つの番号を選択して赤または白のどちらかを対応させるから,
通りである. また, 黒玉が含まれていない場合は, 個の玉の番号は
組だけ同じで, 他の
つの番号はすべて異なっていなければならないので,
通りである.
得点が 点の場合も検算のためにここでやっておくと, まず, 黒玉が含まれている場合, 残り
個の玉の番号は
組が同じなので,
通りである. また, 黒玉が含まれていない場合は, 個の玉の番号は
組が同じで, 他の
つの番号は異なっているので,
通りである. 以上, すべて合計すると,
なので, よさそうである. 得点が 点の場合が,
通り, 得点が
点の場合が,
通り, 得点が
点の場合が,
通りで, 合計
通りである.
得点が
点である確率は,
得点が 点である確率は,
期待値は,
である.
//