ファインマンの経路積分は難しいけれども, ファインマンの微分は, 大学入試問題にも使える. 年の大阪大学理系の問題から.
【問】

【解】
のとき,
だから,
である. 対数関数は単調増加だから,
のとき,
,
のとき,
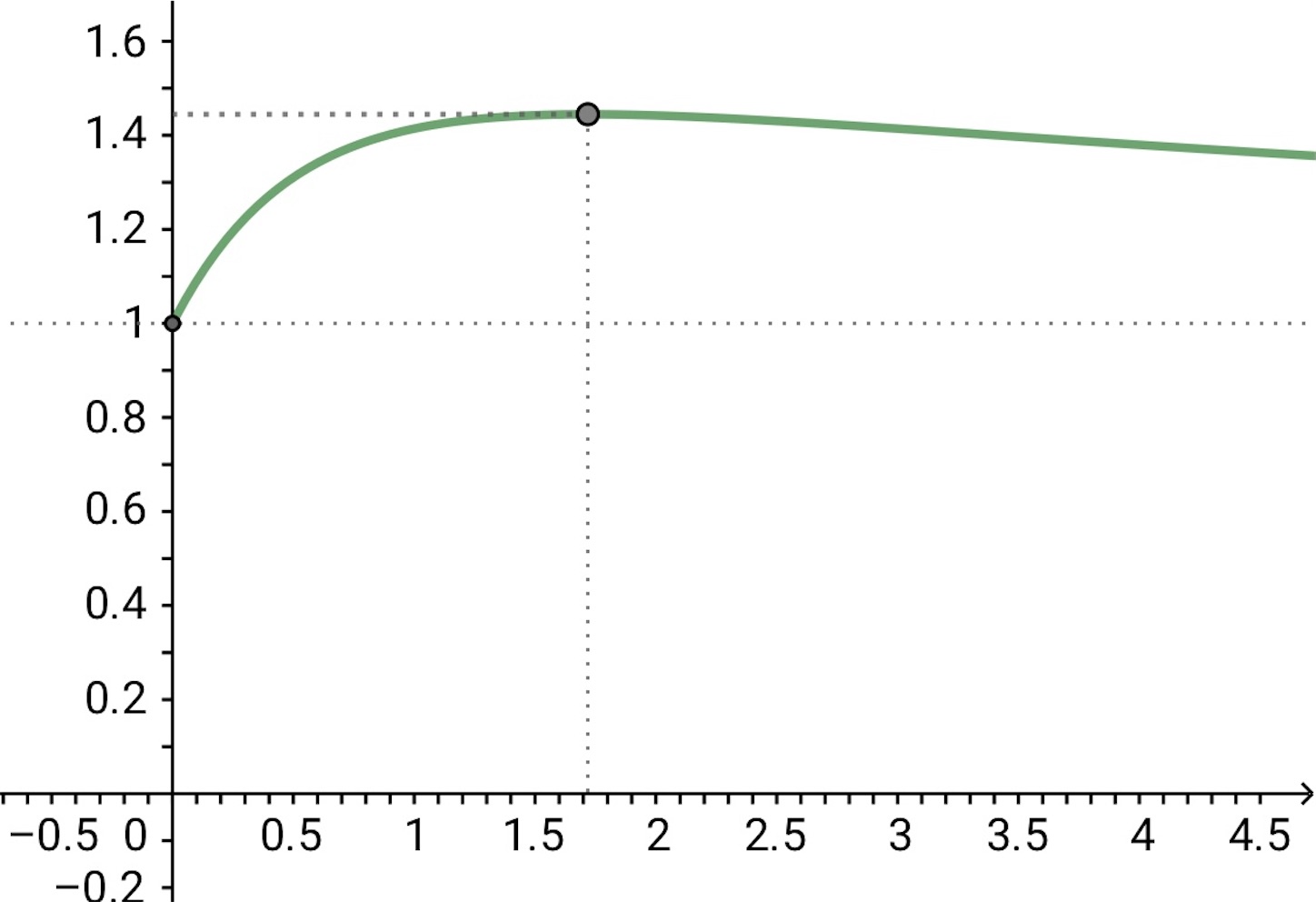
である. したがって,
は,
で最大値
をとる.
と表わすことができるから,
したがって,
一方,
//
ファインマンの経路積分は難しいけれども, ファインマンの微分は, 大学入試問題にも使える. 年の大阪大学理系の問題から.
【問】

【解】
のとき,
だから,
である. 対数関数は単調増加だから,
のとき,
,
のとき,
である. したがって,
は,
で最大値
をとる.
と表わすことができるから,
したがって,
一方,

//