陥没地帯 (236) - ノリの悪い日記

有限増分定理は, 森毅の著作「現代の古典解析」で知った. 彼が訳したディユドネの「現代解析の基礎」では, 平均値の定理として「有限増分定理」を紹介している. ディユドネは,

平均値の定理の真価は等式にあるのではなく, 不等式にあるのだ.

と書いている. 有限増分定理は, このような問題の場合, 数 $\mathrm{III}$ で習う積分の不等式 (積分の単調性) を使って示せばよい. $2005$ 年東大理系前期の問題.

【問】
f:id:noriharu-katakura:20210927101208j:plain

【解】
$(1)$
$\displaystyle{f'(x) = \frac{1}{2}+\left(\frac{1}{2}-x\right)e^{-2(x-1)}}$
$\displaystyle{f''(x) = 2(x -1)e^{-2(x-1)}}$

$\displaystyle{f''(1) = 0}$

$x < 1$ のとき,
$\displaystyle{f''(1) < 0}$

$x > 1$ のとき,
$\displaystyle{f''(1) > 0}$

$\displaystyle{f'(1) = 0}$
$\displaystyle{f'\left(\frac{1}{2}\right) = \frac{1}{2}}$
$\displaystyle{\lim_{x \to \infty} f'(x) = \frac{1}{2}}$

(増減表を書いて) したがって, 題意を満たす.

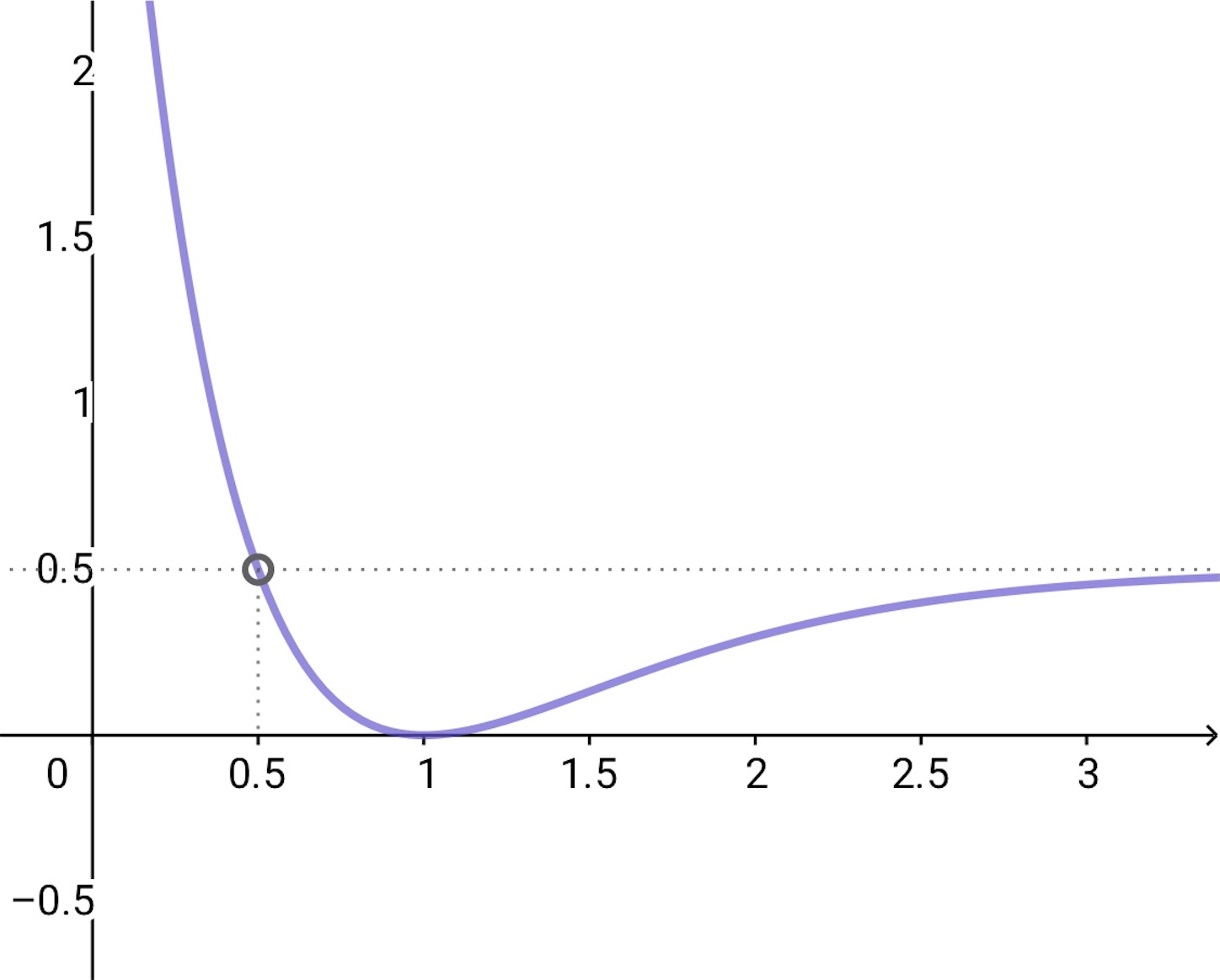
f:id:noriharu-katakura:20210927101413j:plain

$(2)$

$\displaystyle{f\left(\frac{1}{2}\right)= \frac{1+e}{4} > \frac{1}{2}}$

で, $f(x)$ は単調増加であり, すべての $n$ について

$\displaystyle{f(x_n) > \frac{1}{2}}$

である. また $(1)$ の結果から, $f'(x)$ は連続で,

$\displaystyle{0 \leq f'(x_n) < \frac{1}{2}}$

である. また, $f(1)= 1$ だから,

$\begin{align} |x_{n+1}-1| &= |f(x_n) -f(1)| \\&= \left|\int_{1}^{x_n}f'(x)dx\right| \\&\leq \frac{1}{2}\left|\int_{1}^{x_n}dx\right| \\&= \frac{1}{2}|x_n - 1| \end{align}$

再帰的に繰り返して,

$\displaystyle{ 0 \leq |x_{n}-1| \leq \left(\frac{1}{2}\right)^n|x_0 - 1| }$

を得る.

$\displaystyle{\lim_{n \to \infty} \left(\frac{1}{2}\right)^n|x_0 - 1| = 0}$

だから, $\displaystyle{x_0 > \frac{1}{2} }$ のとき,

$\displaystyle{\lim_{n \to \infty} x_n = 1}$

である.
//

※
$\displaystyle{\lim_{x \to \infty} f'(x) = \lim_{x \to \infty} \left\{\frac{1}{2}+\left(\frac{1}{2}-x\right)e^{-2(x-1)}\right\}}$

を求めるのに, $\displaystyle{\lim_{x \to \infty }xe^{-2(x-1)}=0}$ の証明をわざわざ書くまでもないと思うが, もしロピタルの定理も使わずに書くとしたら, まず,

$\displaystyle{\lim_{n \to \infty }n\left(\frac{1}{e}\right)^{2(n-1)}=0}$

を証明するために, $e = 1+ h$ ( $h > 0$ ) とおく. $2$ 項定理より,

$\begin{align}(1+ h)^{2(n-1)} &> \frac{1}{2}(2n-2)(2n-3)h^2 \\&= (n-1)(2n-3)h^2 \end{align}$

したがって,

$\displaystyle{0< n\left(\frac{1}{e}\right)^{2(n-1)}< \frac{n}{ (n-1)(2n-3)h^2}}$

から, $n \to \infty$ とすれば,

$\displaystyle{\lim_{n \to \infty }n\left(\frac{1}{e}\right)^{2(n-1)}=0}$

となる. 次に, $n \leq x < n +1$ となるように, $n$ をとると, $x \to \infty$ のとき, $n \to \infty$ になるが,

$\displaystyle{\displaystyle{ 0< x\left(\frac{1}{e}\right)^{2(x-1)}< (n+1)\left(\frac{1}{e} \right)^{2n}e^2} }$

となって, $x \to \infty$ とすれば,

$\displaystyle{\lim_{x \to \infty }xe^{-2(x-1)}=0}$

をえる. //

※ 有限増分定理とは, $f(x)$ が $a$ , $b$ を含むある開区間で微分可能として,

$m \leq f'(x) \leq M$ ( $a \leq x \leq b$ )

とすると,

$m(b -a) \leq f(b) - f(a) \leq M(b - a)$

が成り立つということである.

たとえば, $f'(x) \leq g'(x)$ が成立している場合,

$f'(x)- g'(x) \leq 0$

として, $F(x) = f(x)-g(x)$ とおけば,

$F'(x) \leq 0$

ということなので, 定理より,

$F(b) - F(a) \leq 0$

つまり,

$f(b)-f(a) \leq g(b) - g(a)$

が成り立っている.

森毅は, さらに

$(\alpha - \epsilon) g'(x) \leq f'(x) \leq (\alpha + \epsilon)g'(x)$

ならば,

$(\alpha - \epsilon) (g(x)-g(a)) \leq f(x)-f(a) \\ \leq (\alpha + \epsilon)(g(x)-g(a))$

から, ロピタルの定理,

$\displaystyle{\lim_{x \to a}\frac{f'(x)}{g'(x)} = \alpha}$

ならば ( ただし, $x \neq a$ で $g'(x) \neq 0$ ),

$\displaystyle{\lim_{x \to a}\frac{f(x)-f(a)}{g(x) - g(a)} = \alpha}$

を得ている. (もちろんロピタルの定理は特定の不定形に使うものであり, この場合 $f(a)=g(a)=0$ である.)
//