方べきの定理とその逆を使うと, 作図に便利なことがある. 特に, ここで扱う作図題で重要なのは,
の辺
の延長上の
点を
とするとき,
ならば, 直線
は, 円
に接する.
ということである.
まずは, 基本的な例題. 与えられた 点を通り, 与えられた直線に接する円を作図する.
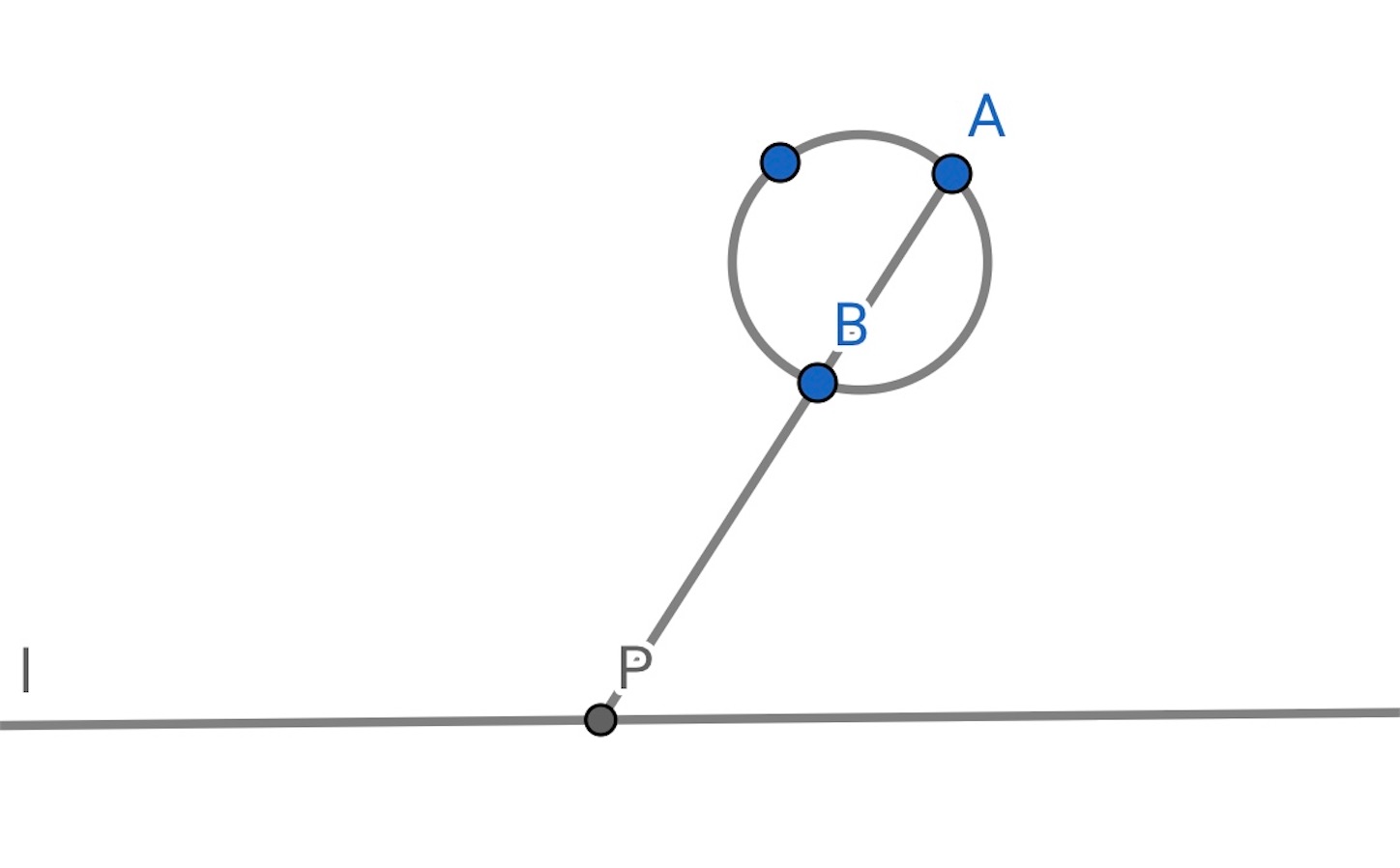
なにはともあれ, と
を通る直線を書き, 直線
の交点を
とする.
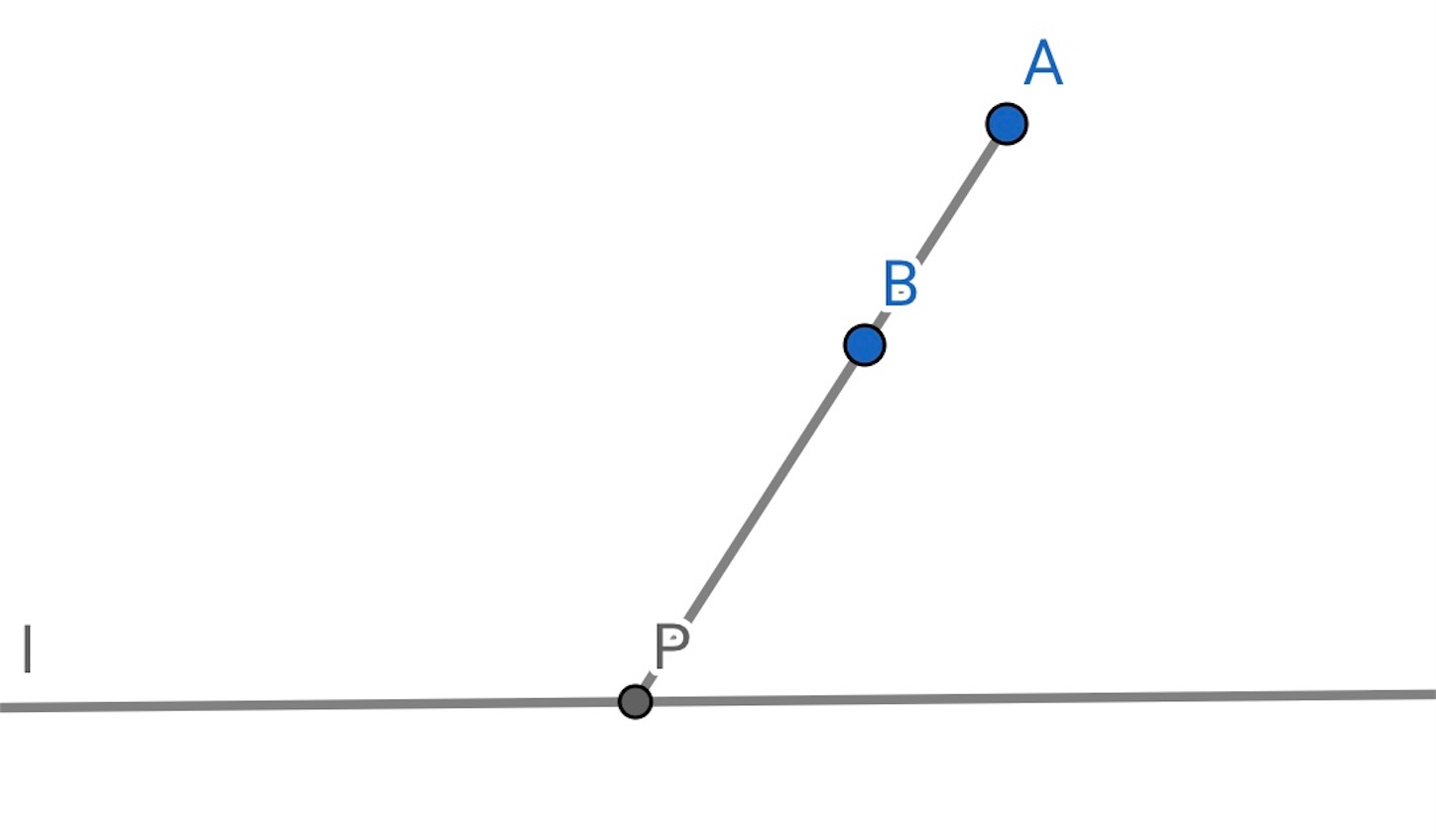
目指すのは方べきの定理の利用なので, ,
を通る円を適当にもう
点決めて
点を通る円を図示する (円は
点で決まる). 円は
,
さえ通ればなんでもよい.
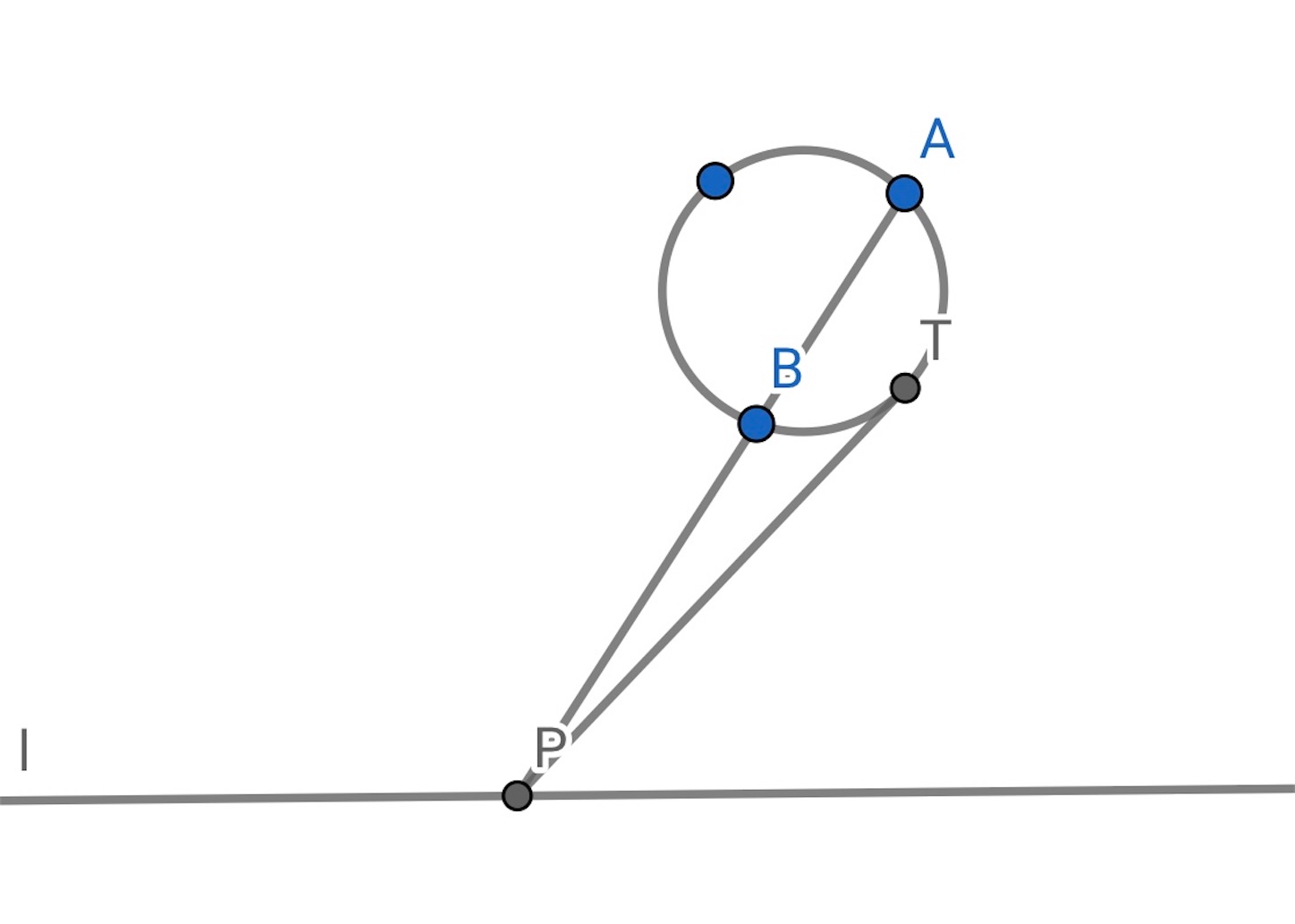
作った円に を通る接線を引く. 接線の長さは等しいので,
本引けば十分である.
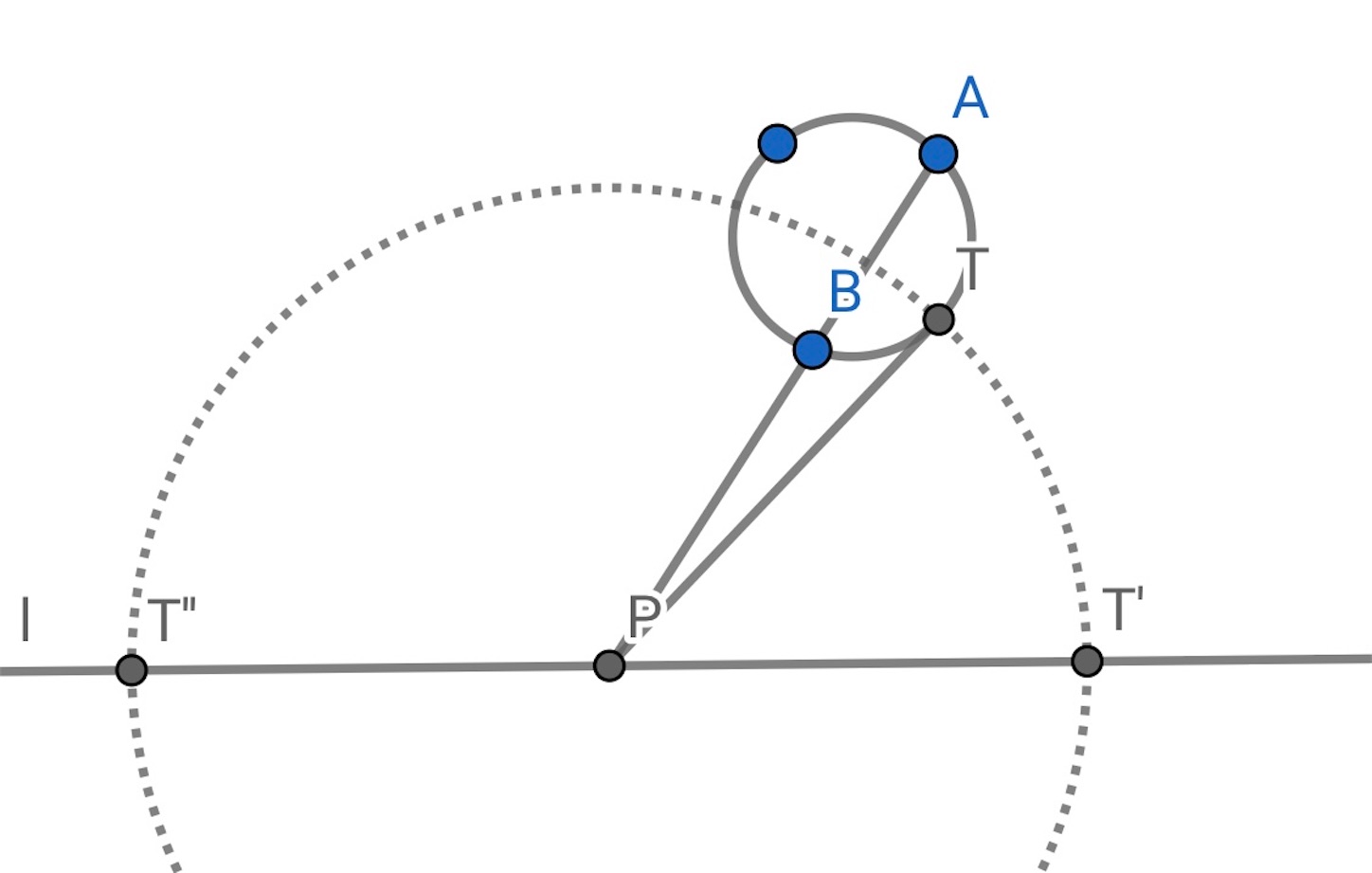
を中心として,
を半径とする円を引き, 直線
との交点を
,
とする.
,
,
を通る円を書けば所望の円が得られる.
,
,
を通る円も題意を満たす.
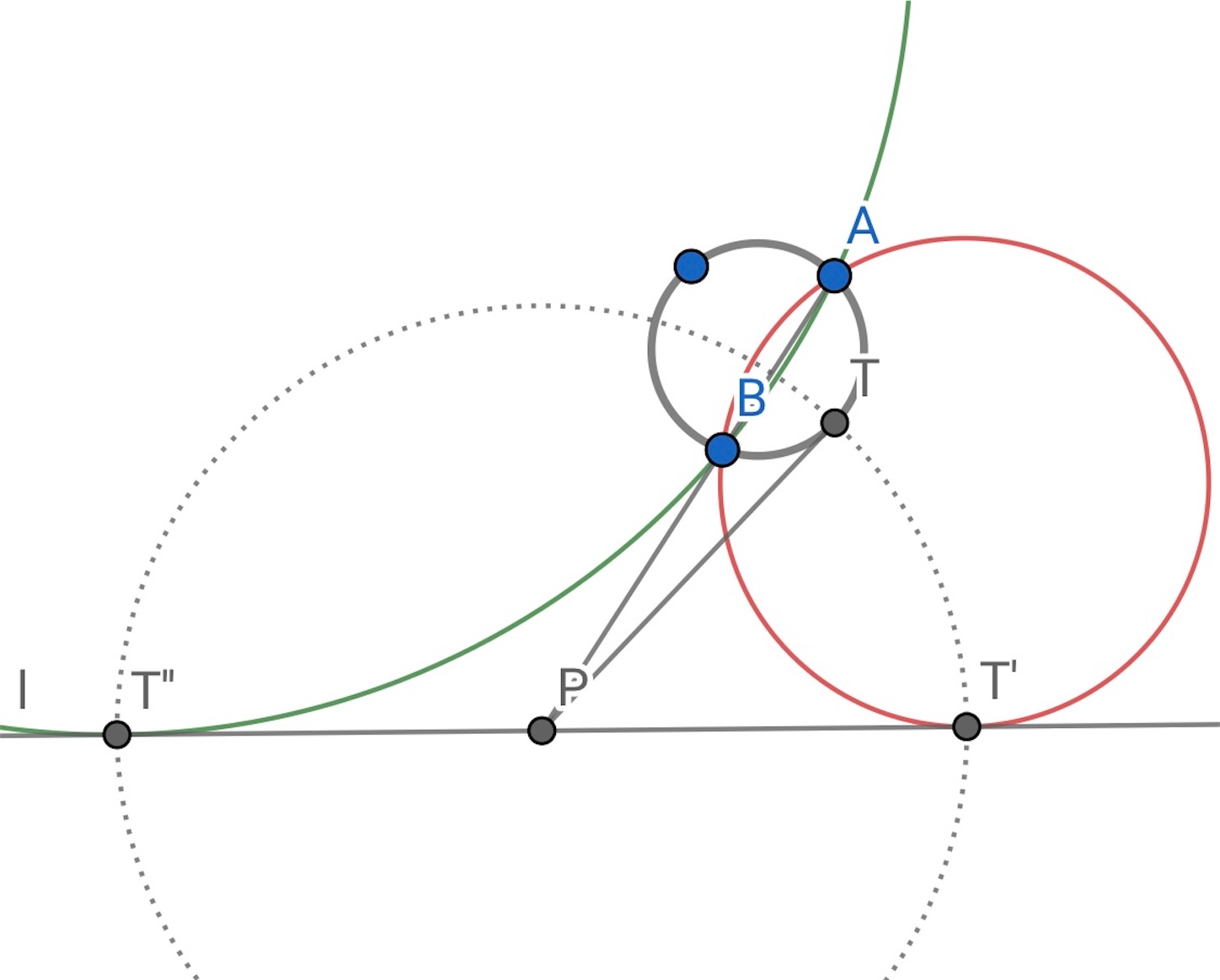
もちろん, 円周上の点で が作れるのならば, どこでもよい.
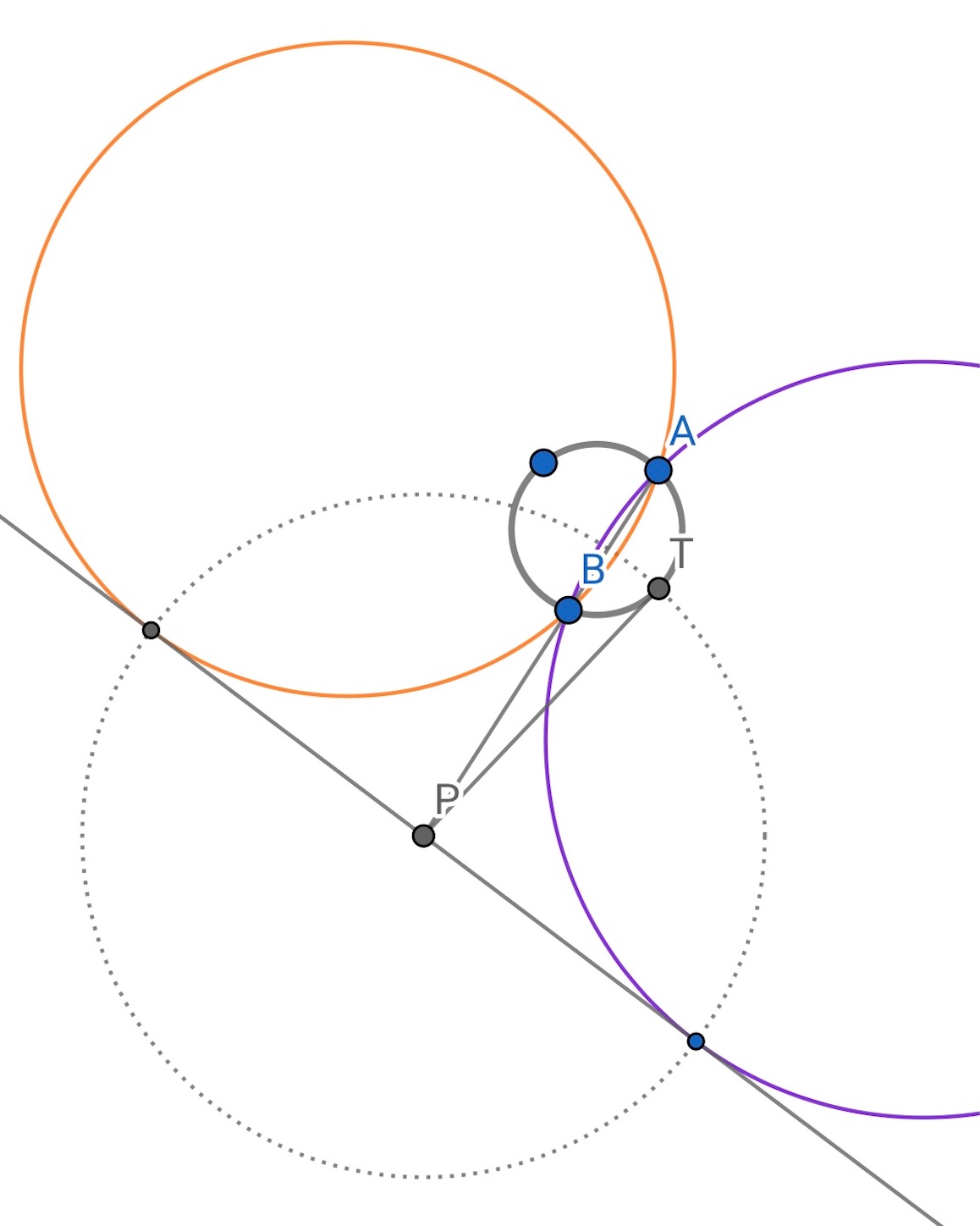
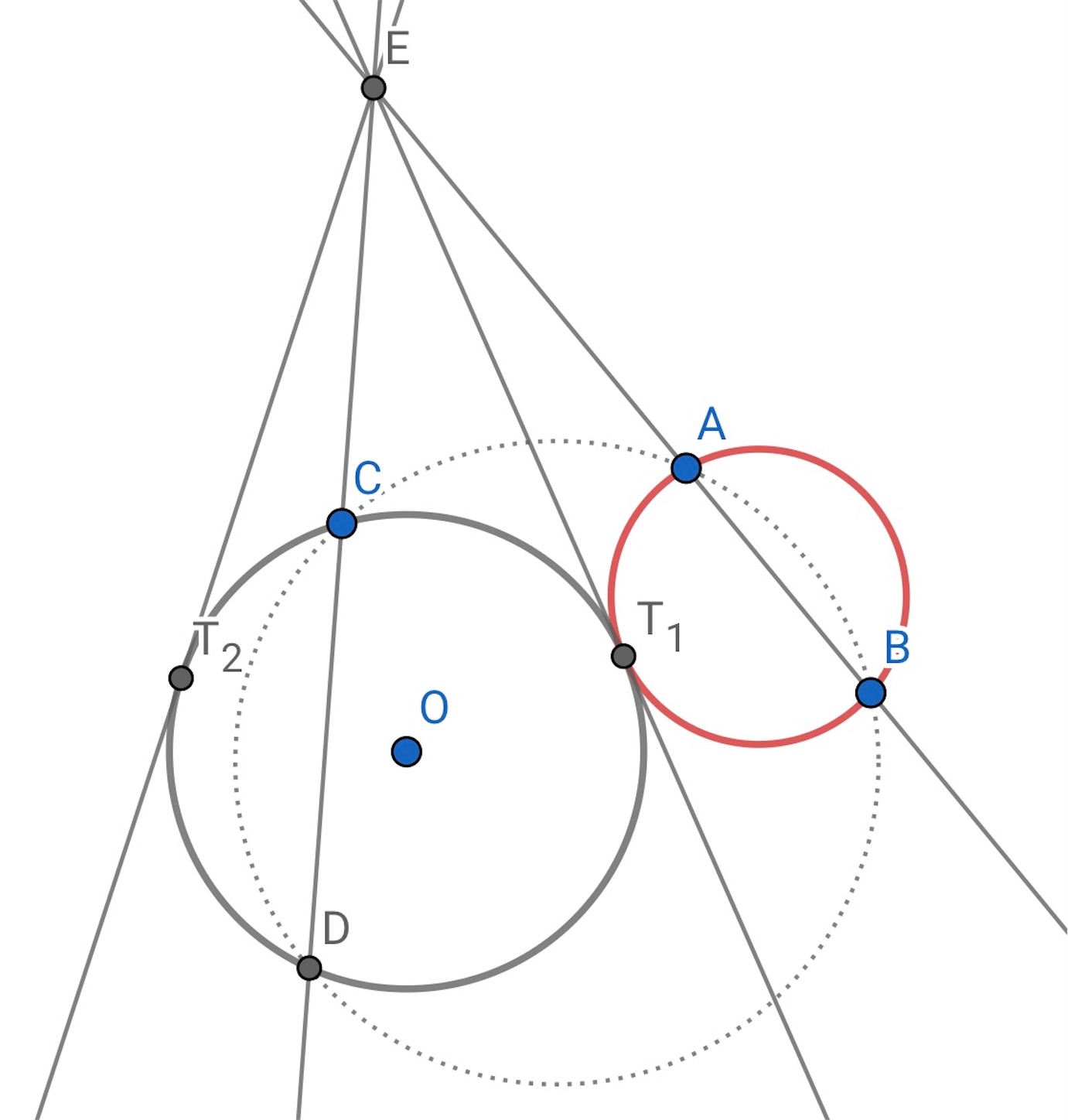
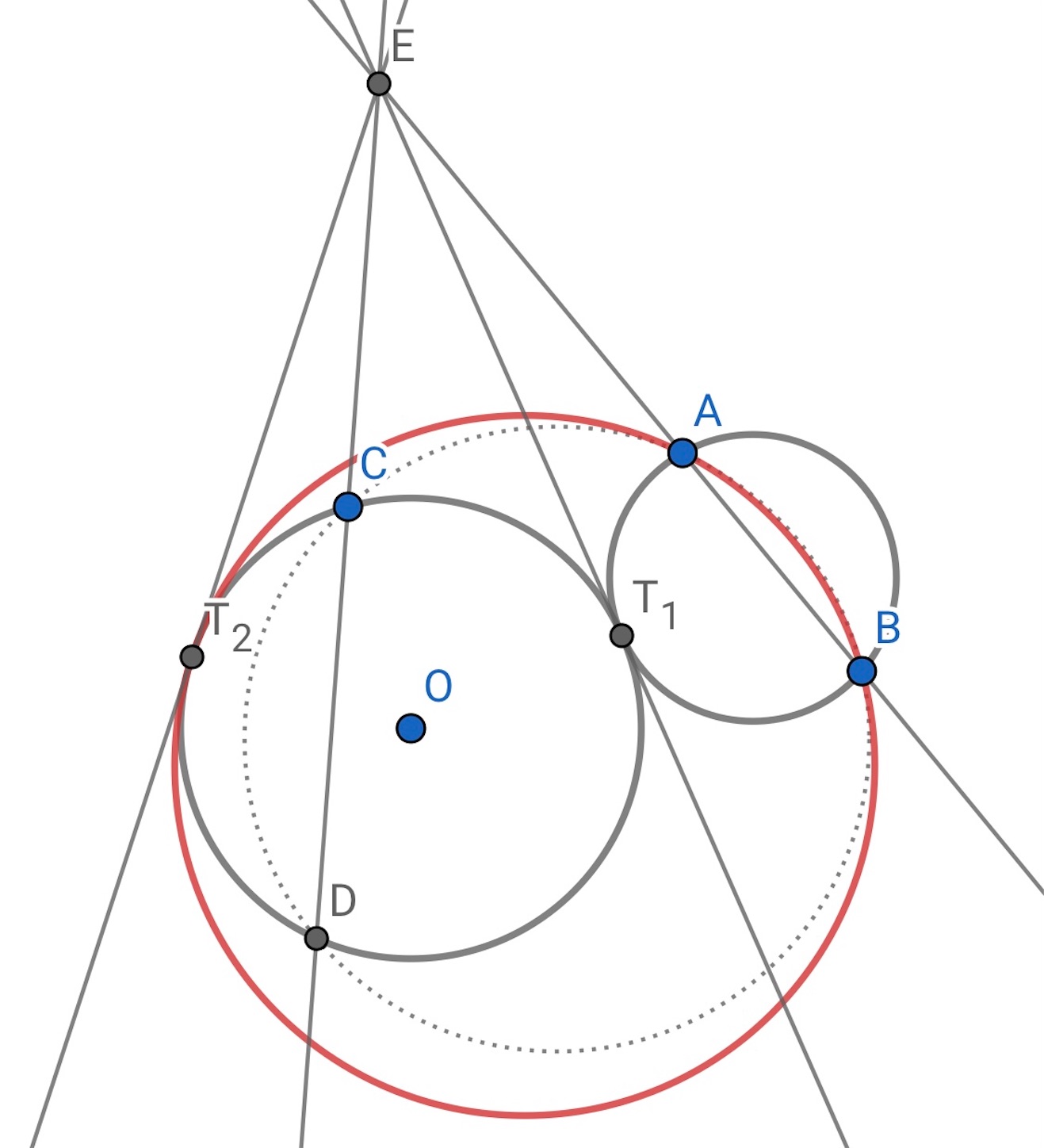
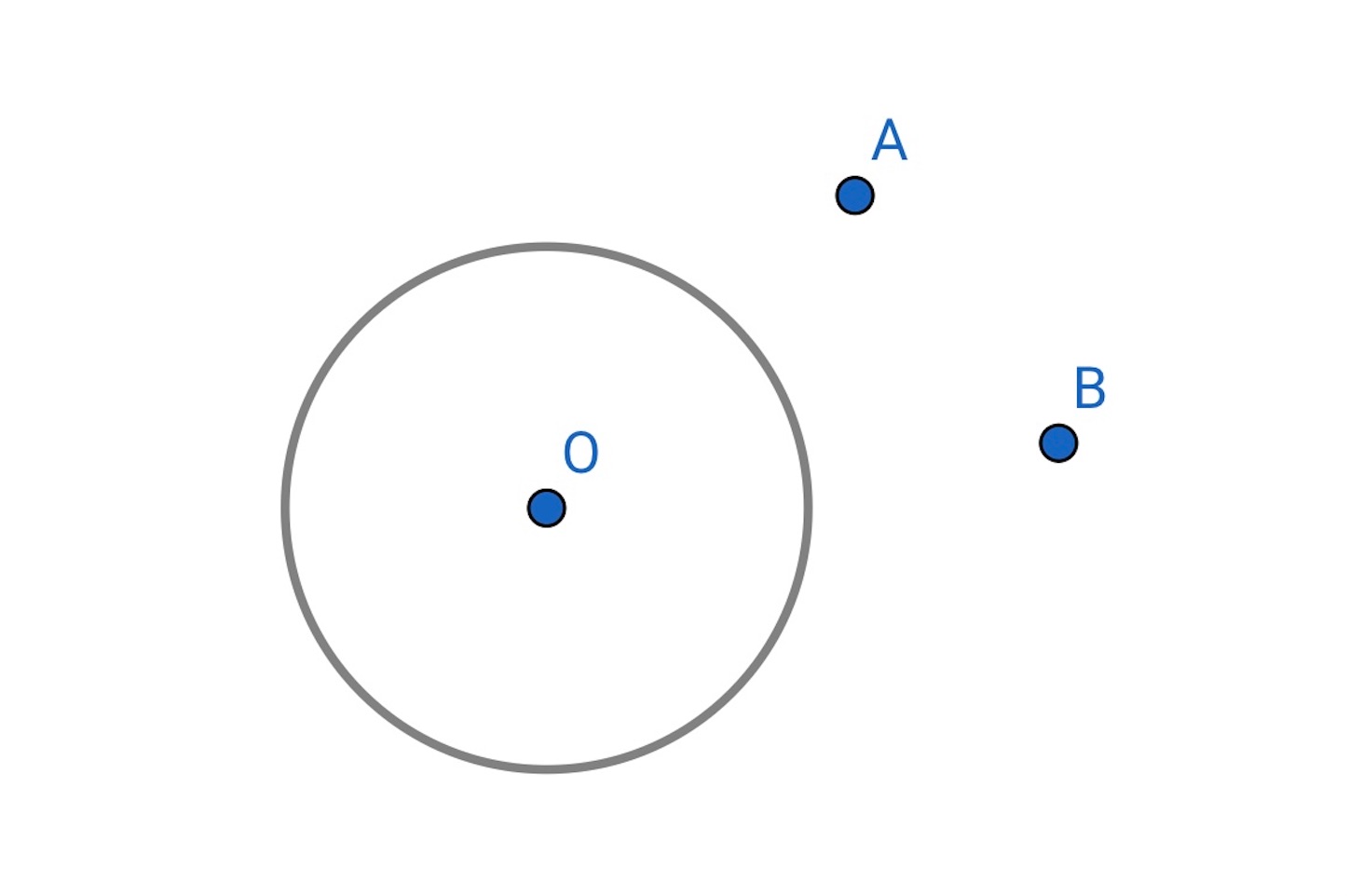
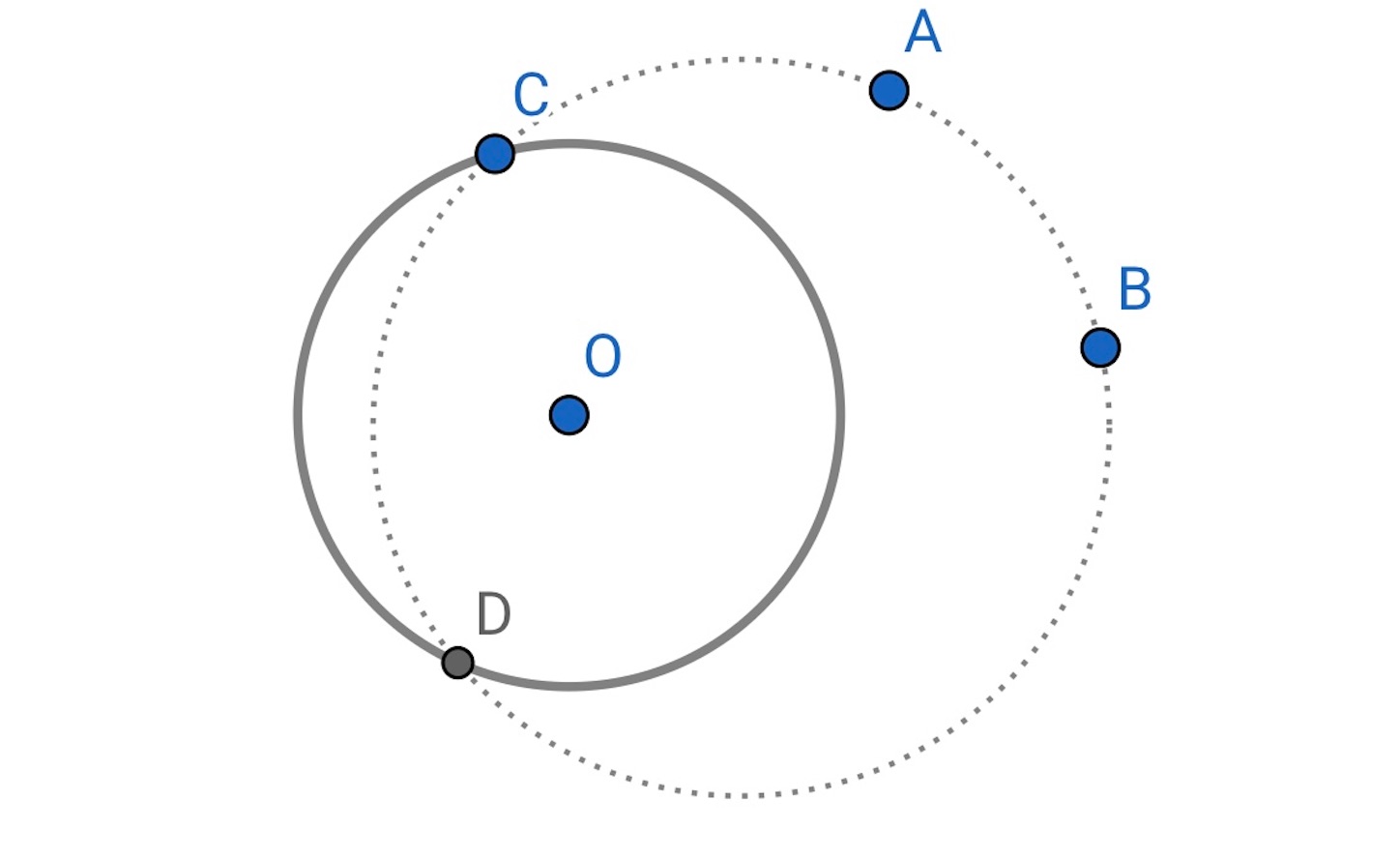
今度は与えられた 点を通り, 与えられた円に接する円を作図する.
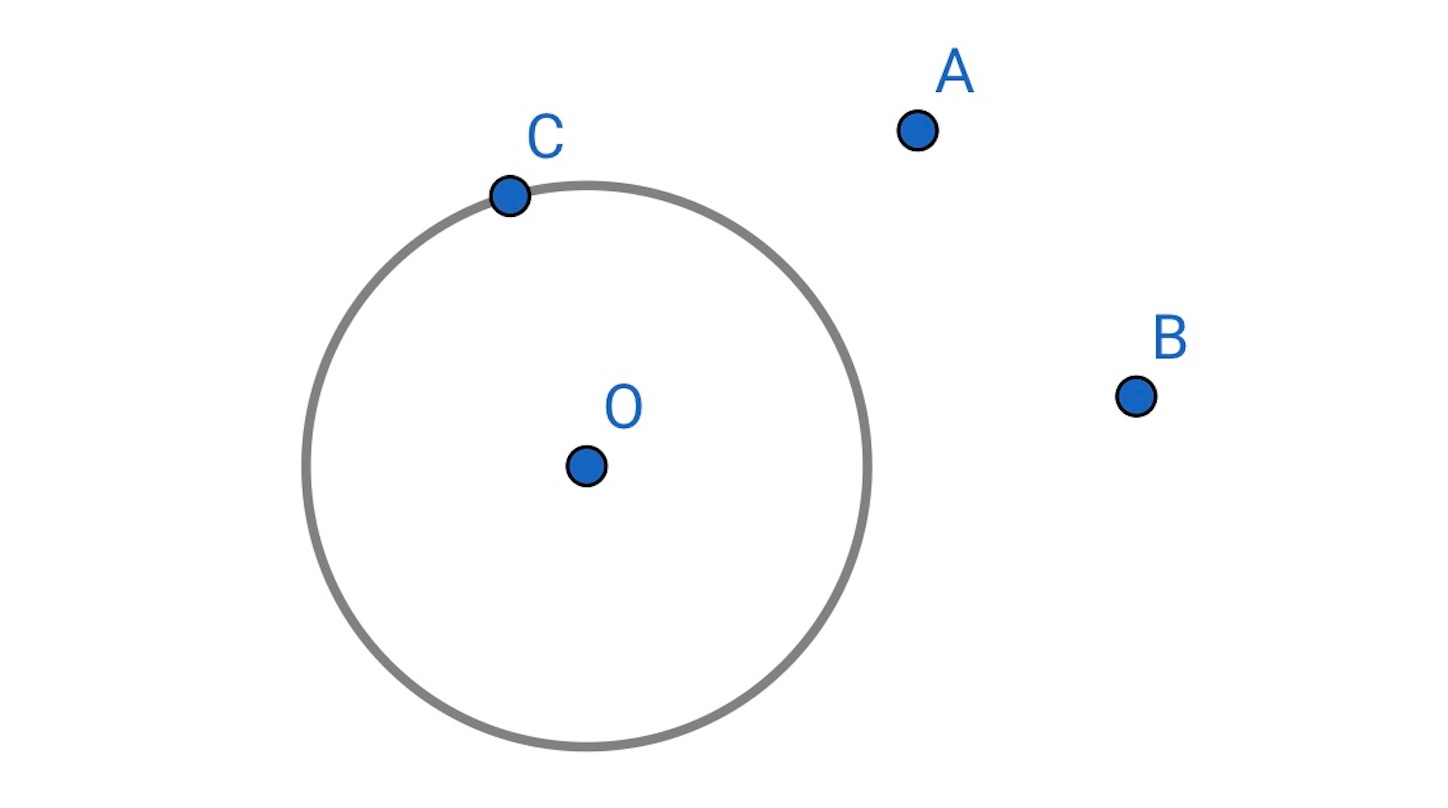
まず, 与えられた円の周上に 点
をとる.
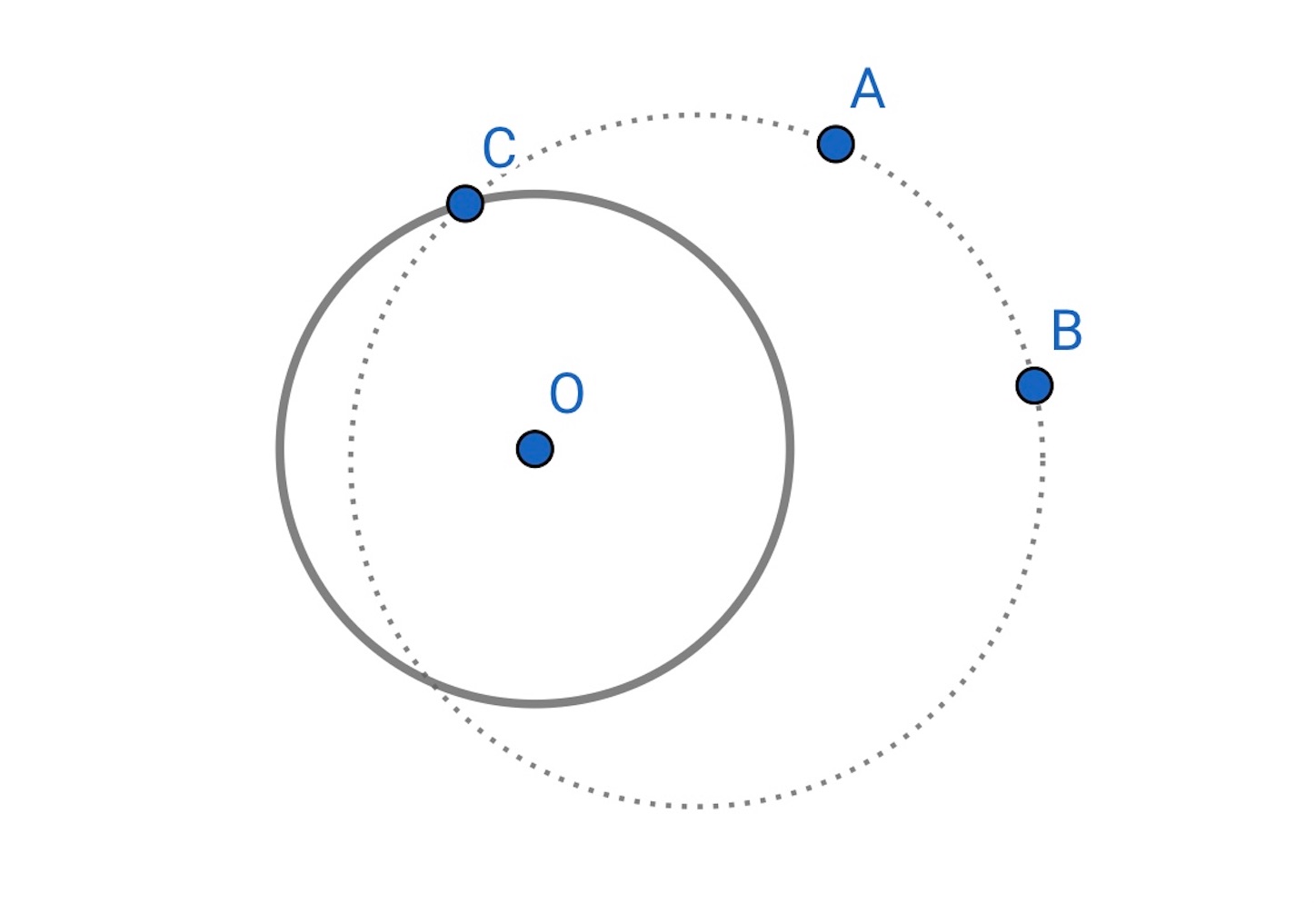
,
,
を通る円を描く.
与えられた円とのもう一つの交点を とする.
,
と
,
を通る直線をそれぞれ書き, 交点を
とすると, 方べきの定理が使えそうである.
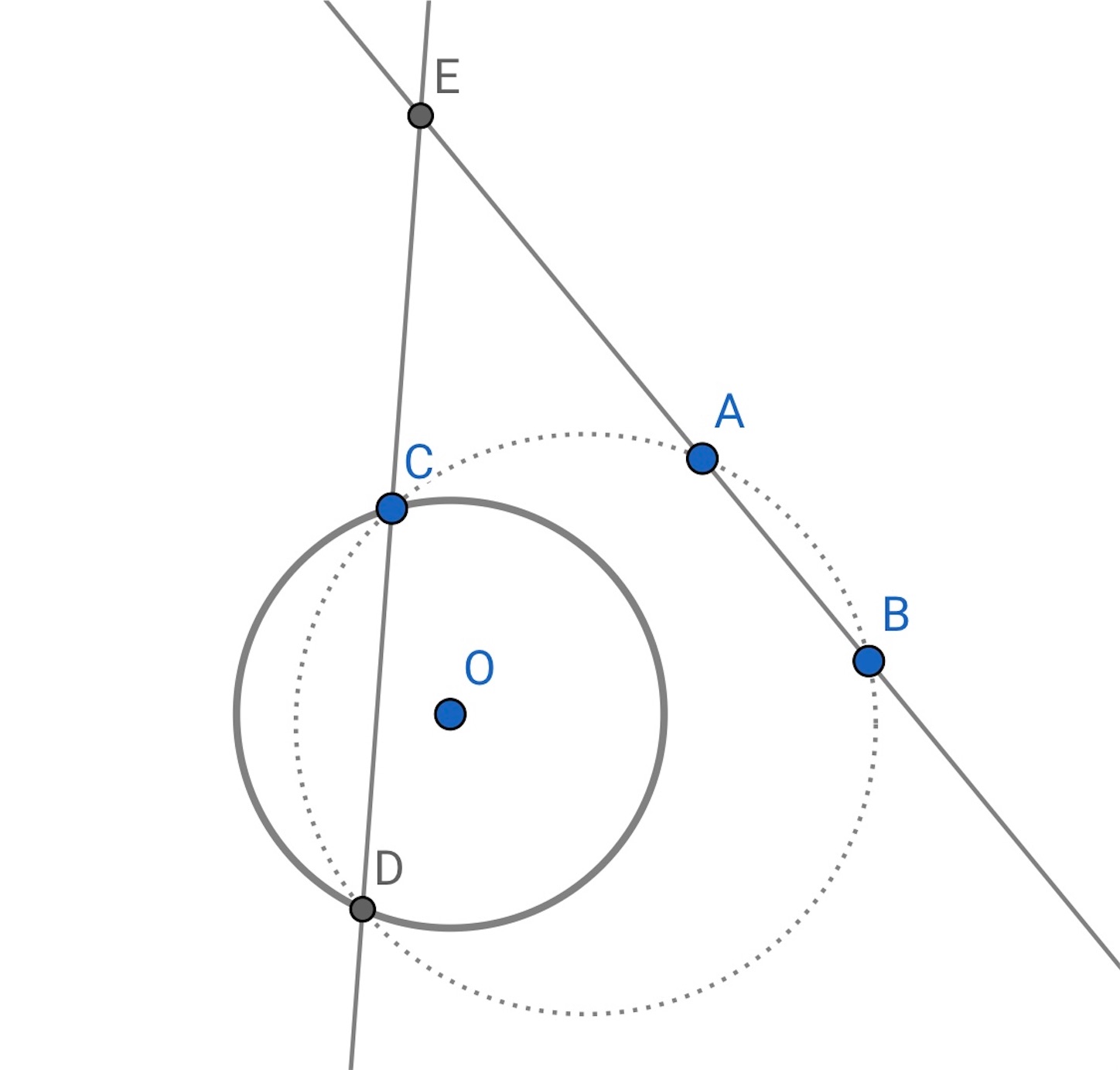
から与えられた円に接線を引き, 得られる二つのそれぞれの接点と,
,
を通る円をスクリーンに表示させると, その円は題意を満たす.