陥没地帯 (177) - ノリの悪い日記

前の記事の続き. 極と極線については, もう少し準備がいる.

円 $O$ について点 $P, Q$ が「互いに共軛である」とは, 極 $P$ の極線上に極 $Q$ があり, $Q$ の極線上に極 $P$ があることをいう.

前の記事の図を見ればそうではないかと想像できる次の事実は共軛に関して基本的である.

点 $P$ , $Q$ が円 $O$ に関して共軛であることと, $PQ$ を直径とする円が円 $O$ と直交することは同値である.

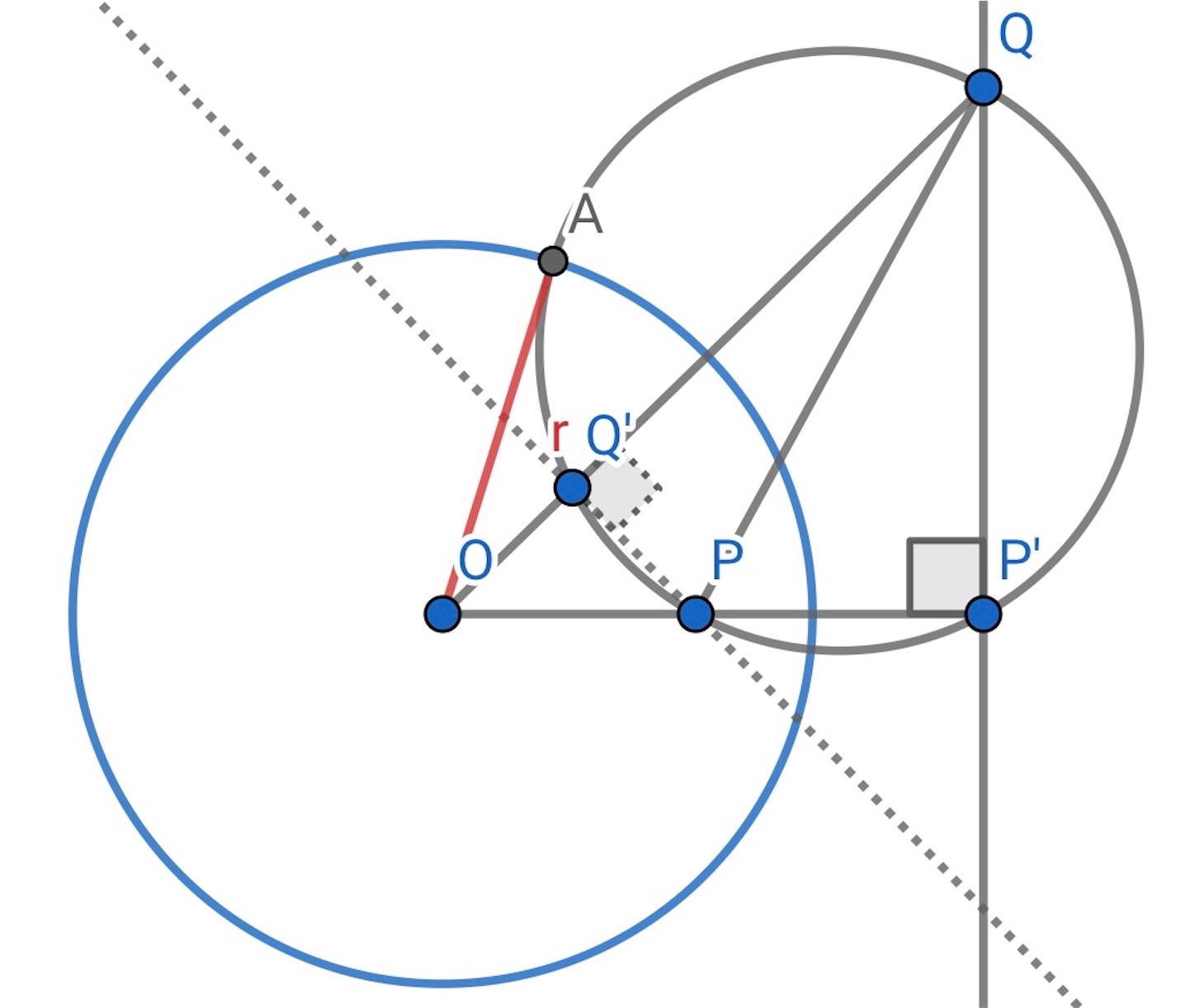
f:id:noriharu-katakura:20210512233807j:plain

まずは, 点 $P$ , $Q$ が円 $O$ に関して共軛であると仮定する. 点 $P$ を円 $O$ に関して反転した $P'$ は $PQ$ を直径とする円の周上の点である. $P$ , $P'$ は一方が円 $O$ の内部にあれば, 他方は外部だからこの円は, 円 $O$ と交点をもつ. その交点のひとつを $A$ とすると, $OP\cdot OP' = OA^2 = r^2$ だから, 方べきの定理の逆から $2$ つの円は直交している.

逆に, $PQ$ を直径とする円が円 $O$ と直交していると仮定する. そうすると $OA$ は直径 $PQ$ の円と接しているから, 方べきの定理より $OP\cdot OP' = OA^2 = r^2$ であり, $PQ$ は直径だから, $\angle PP'Q = 90^\circ$ である. したがって $P$ , $Q$ は共軛である.//

いままで曖昧かつ完全に間違えていた問題の証明を再度したいので, もうひとつだけ準備する.

「円 $O$ の弦 $AB$ を調和に $P$ , $Q$ が分ければ, $P$ , $Q$ は共軛である.」

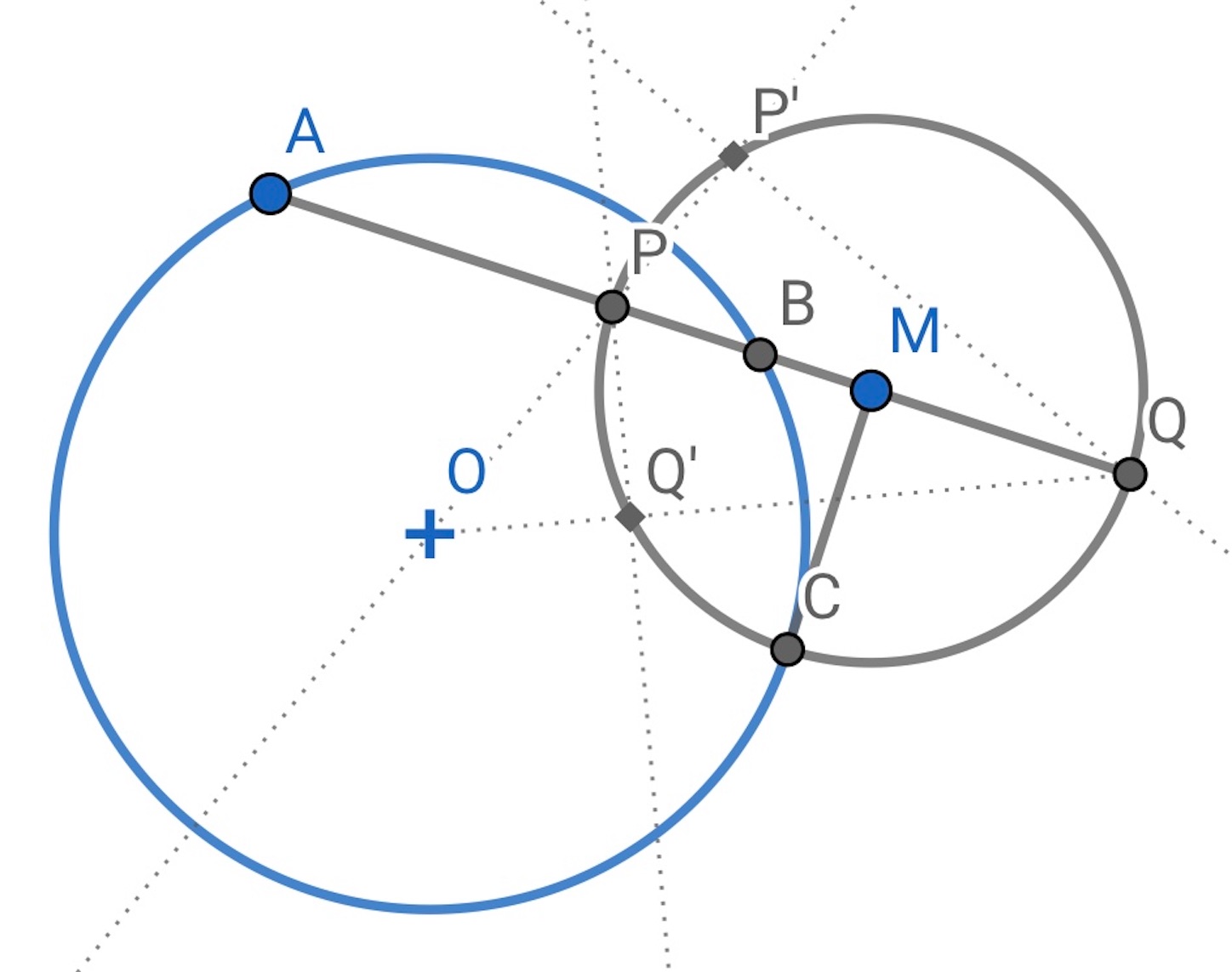
f:id:noriharu-katakura:20210513005409j:plain

$PQ$ を $A$ , $B$ が調和に分けているとも見ることができるので、 $PQ$ の中点 $M$ をとって

$MP^2 = MA \cdot MB$

だが, 円 $O$ と $PQ$ を直径とする円の交点のひとつを $C$ とすれば, $MP = MC$ なので, $2$ つの円は直交する. $PQ$ は直径なので, 直前の結果から $P, Q$ は共軛である.//
※ 逆も成立する.

以上で前の問題をきちんと証明する. 条件を確認しておくと $A$ , $P$ , $B$ , $Q$ は調和点列であった. $A'$ , $B'$ , $Q$ は同一直線上の点である. (前の図をそのまま使ったが, $G$ は使わない.)

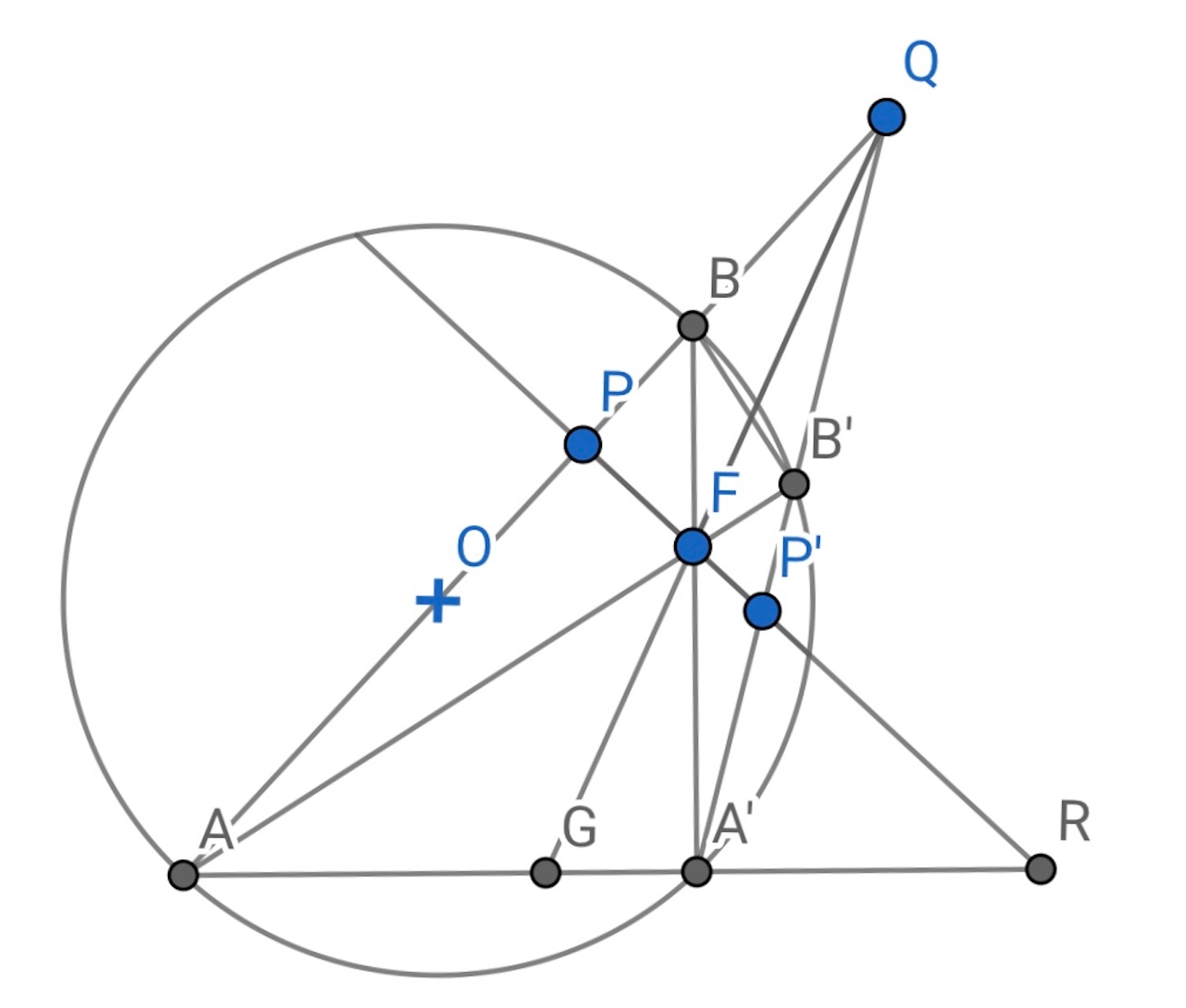
f:id:noriharu-katakura:20210513010824j:plain

円 $O$ に内接している四角形 $ABB'A'$ の対角線の交点を $F$ とする. $PF$ の延長線と $AA'$ の交点を $R$ とする. そうするとメネラウスの定理を三角形 $ABA'$ とそれを切る $PR$ に使って

$\displaystyle{\frac{BP}{PA}\cdot \frac{AR}{RA'} \cdot \frac{A'F}{FB} = 1}$

チェバの定理の逆 *1を利用して $BB'$ の延長線が $R$ を通ることを証明する. 三角形 $ABA'$ と点 $B'$ について, $AB'$ が $BA$ と $F$ で交わり, $A'B'$ が $AB$ と $Q$ で交わっているとき, $BB'$ が $AA'$ と $R$ と交わるかを調べる. すなわち, メネラウスの定理の結果と $A$ , $B$ , $P$ , $Q$ が調和点列であることを使って,

$\displaystyle{\frac{BF}{FA'}\cdot \frac{A'R}{RA} \cdot \frac{AQ}{QB} \\ = \frac{BF}{FA'}\cdot \frac{BP}{PA} \cdot \frac{A'F}{FB} \cdot \frac{AQ}{QB} }$
$\displaystyle{= \frac{BP}{PA} \cdot \frac{AQ}{QB}\\ =1 }$

となるので, $BB'$ の延長線は $R$ を通る.

そうすると $R$ または $F$ からの線束を考えれば, $A'$ , $P'$ , $B'$ , $Q$ も調和点列である.
※ 点 $F$ からの線束だと $BB'$ の延長線が $R$ を通る証明は蛇足だが, まあしておいた.

$A$ , $P$ , $B$ , $Q$ も $A'$ , $P'$ , $B'$ , $Q$ も調和点列なので, $Q$ は $P$ と共軛であり, また $P'$ とも共軛である. したがって $Q$ の極線の上に. 極 $P$ と $P'$ もある. したがって $PP'$ は $Q$ の極線と一致する.//

*1:三角形 $ABC$ の辺 $BC$ , $CA$ , $AB$ またはその延長上の $3$ 点を $P$ , $Q$ , $R$ とし, $P$ , $Q$ , $R$ のすべて, またはそのうちの一つだけが辺上にあるとする. このとき, $\displaystyle{\frac{BP}{PC}\cdot \frac{CQ}{QA} \cdot \frac{AR}{RB} = 1}$ ならば, $3$ 直線 $AP, BQ, CR$ は $1$ 点で交わるかまたは平行である.