キンリョウヘン。

ユキヤナギがだいぶ咲いた。

ギンヨウアカシア。

(143) (144) からの続き。しかし、昭和 19 年でも「三平方の定理」は、「ピタゴラスの定理」と書かれているなあ。もちろん、昭和七年当時も「ピタゴラスの定理」である。戦中に「ピタゴラスの定理」は「敵性語」なので「三平方の定理」と呼ばれるようになったという説は本当なのだろうか? 本当だとしても当時、言葉として普及していたのだろうか? 第一、ピタゴラスは米国人でもなし。下手人はだれなんだろう。(塾で「ピタゴラスの定理」というとまったく通じない。)
直線と平面の垂直
諸君は既に一直線と一平面との位置の関係には次の三つの場合があることを学んでいる.
(1) 相交る場合
(2) 直線が平面に含まれる場合
(3) 平行なる場合
此の中で (1) の一直線と一平面とが相交る場合には垂直に交る場合と斜に交る場合との二つがある. このことは一つの直線が他の直線と交る場合の二つの場合があるのと同じである.
さて直線が平面に垂直であるとはどんな意味であるのか, 又それに就ての重要な定理並びに応用を研究するのが本号の目的である.
1. 平面の垂線
一直線が一平面に垂直であることの意味を了解するには先づ次の性質に注意することが必要である.
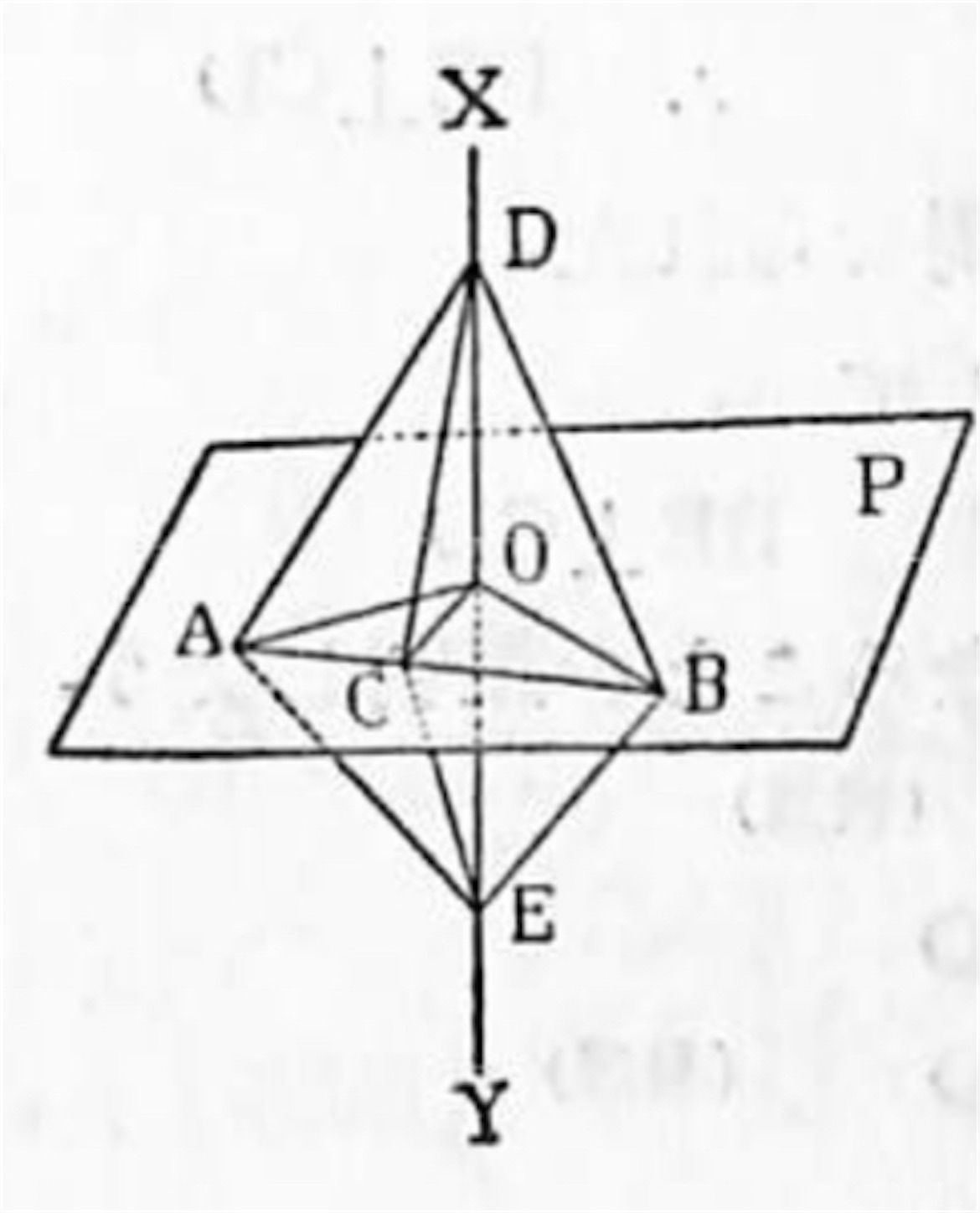
定理 相交る二直線を OA, OB, その二直線の定める平面を P, 又 OA, OB の各に垂直な直線を XY とすれば XY は P 上の総ての直線に垂直となる.
証明: [I] XY が点 O を通る場合
先づ P 上に於て O を通る任意の直線 OC が XY に垂直なることを述べよう.
今 OC と AB との交点を C, 又 XY 上に於て OD = OE とすれば, OC が XY に垂直なるためには ∠DOC = ∠EOC となればよい。
然るに OA, OB は何も DE の垂直二等分線であるから
AD = AE, BD = BE
△ ABD ≡ △ ABE
∴ ∠DAC = ∠CAE
∴ △ DAC ≡ △EAC (二辺と夾角夫々相等)
∴ DC = EC
∴ △ CDO ≡ △EOC (三辺夫々相等)
∴ ∠DOC = ∠ EOC = ∠R となる.
次に P 上に於て O を通らない任意の直線を MN とし, MN に平行に OH を引けば OH は上の証明によって XY に垂直である. 即ち XY ⊥ OH. 然るに OH とXY のなす角は又 XY と OH に平行な MN のなす角であるから XY ⊥ MN となる. 依って XY は P 上の総ての直線に垂直である。
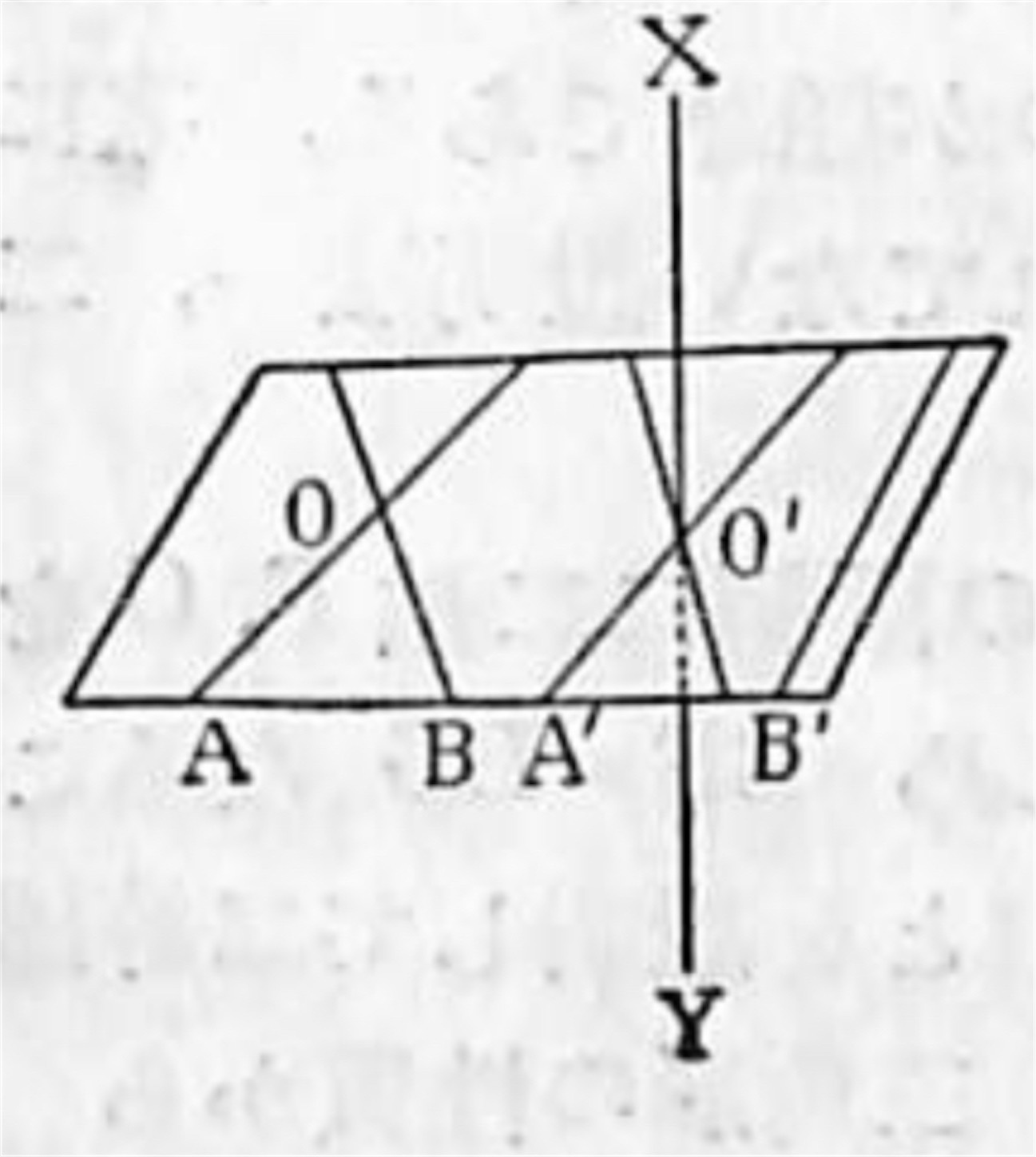
[II] XY が点 O を通らない場合
XY は OA, OB に垂直であるから P に交ることは容易に証明することが出来る.
今此の交点を O' とし, O' を通り二直線 O'A', O'B' を夫々 OA, OB に平行に引けば
OA ⊥ XY 且つ OA ‖ O'A'
∴ XY ⊥ O'A'
OB ⊥ XY 且つ OB ‖ O'B'
∴ XY ⊥ O'B'
依って XY は [I] の証明によって又 P 上の総ての直線に垂直である. ▪️
そして, 平面に出会う直線が, その平面上で交点を通る如何なる直線にも垂直なときは, 此の直線を此の平面の垂線といい, 又此の直線と平面とは垂直であるというから上の研究によって次の定理が成立する.
定理 相交る二直線の各に垂直な直線はこの二直線の定める平面に垂直である.
又垂直でない場合を斜めであるといい, 斜めな直線を斜線ということ及びその出会う点を (垂直の場合にも) 「足」ということも平面幾何の場合と同様である.
2. 三垂線の定理
立体幾何学に於て三垂線の定理といえば平面幾何学に於ける「ピタゴラス」の定理という具合に非常に応用の広い定理である. 次に三垂線の定理とは如何なる定理であるかを述べると共にその応用の一端を研究しよう.
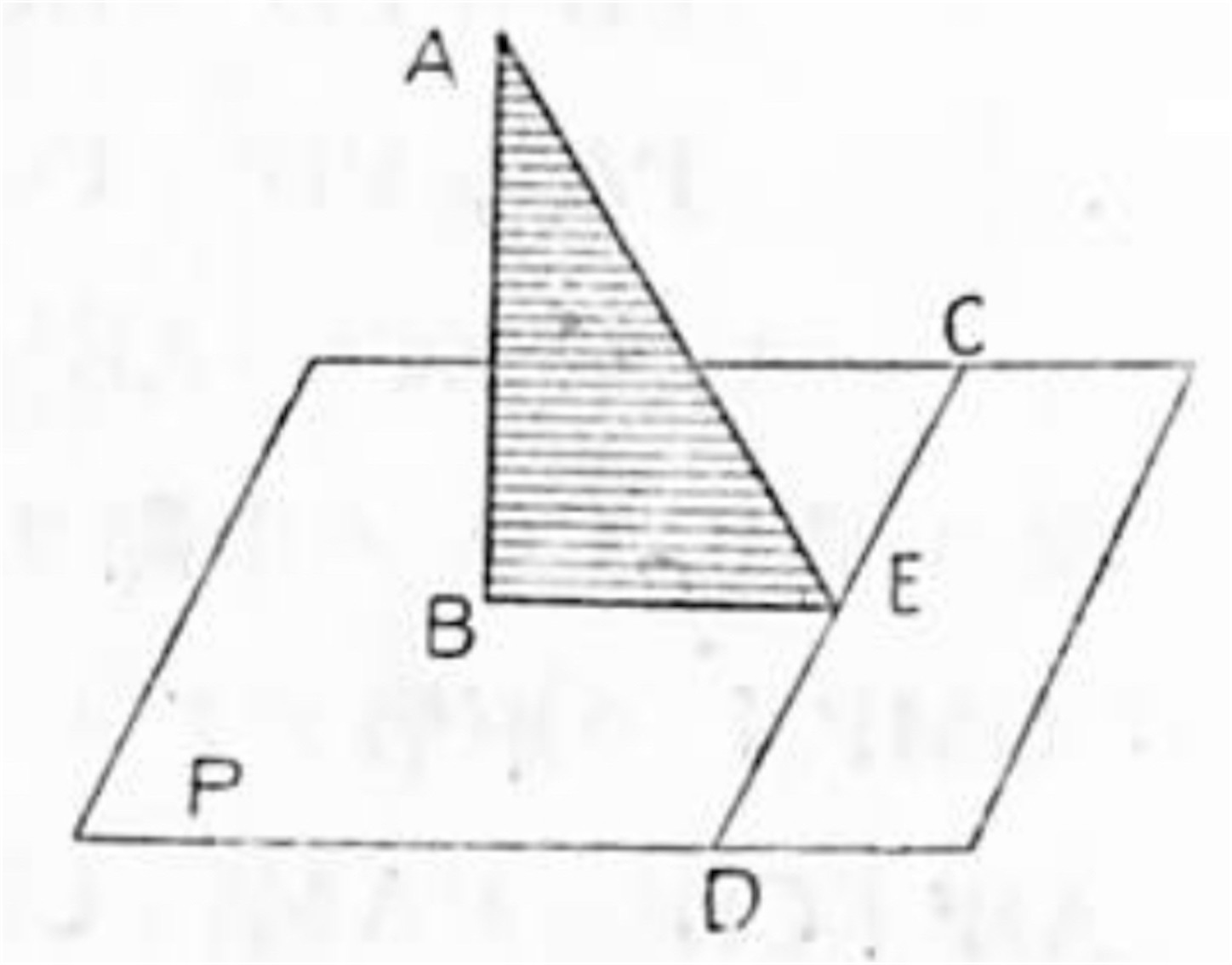
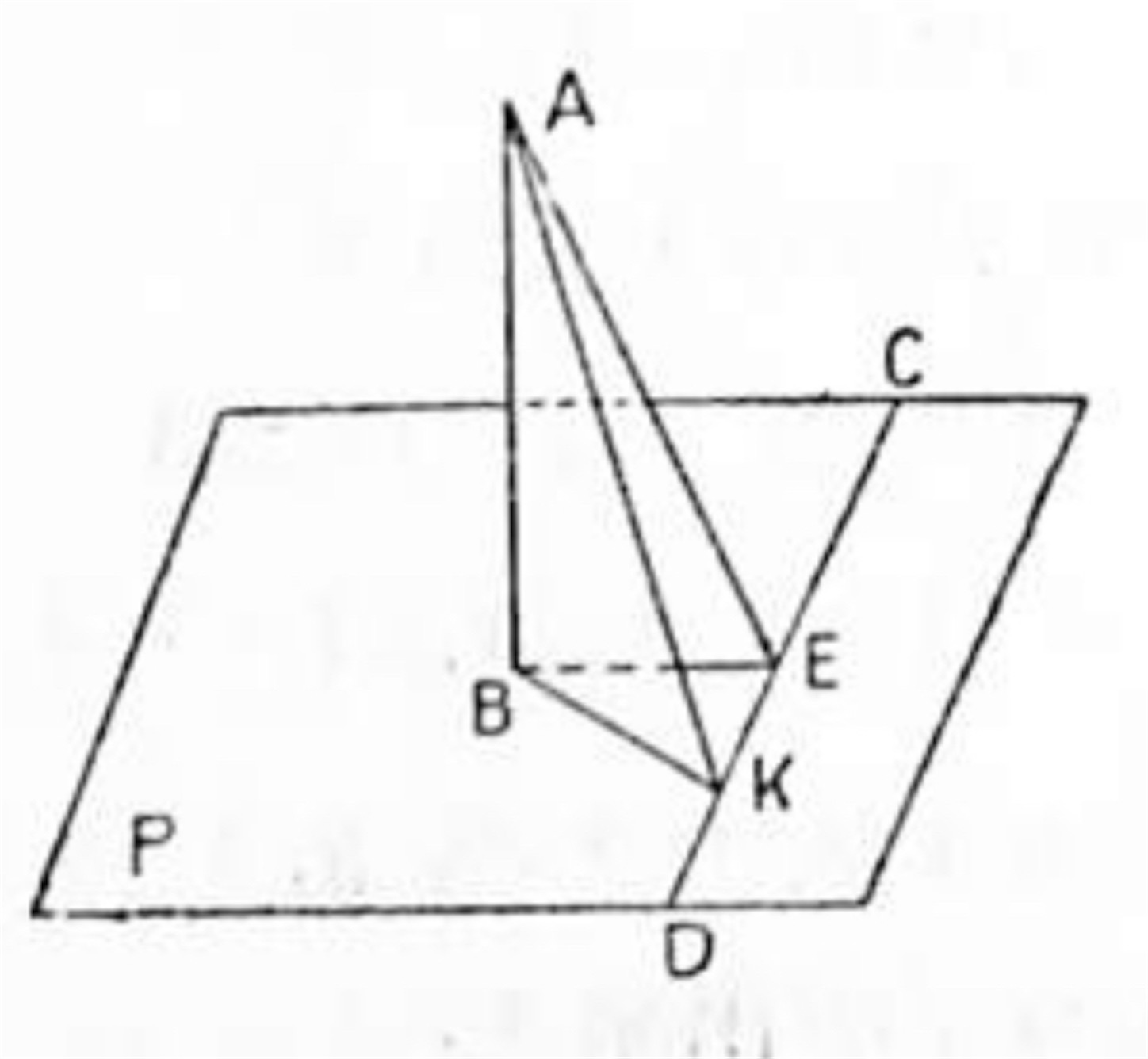
三垂線の定理 平面外の一点からこの平面上の一直線及び平面に垂線を引けば, 其等の垂線の足を結ぶ直線は平面上の其の直線に垂直である.
此の定理の意味は平面 P 外の一点 A から P 上の任意の直線 CD 及び平面 P に夫々垂線 AB, AE を引けば, BE は CD に垂直であるというのである. 先づマッチの軸, 鉛筆, 針金等を用いて机を平面と見做して本定理の真であることを実験して見るがよい.
証明:
AB は平面 P に垂直であるから, AB は平面 P 上のすべての直線に垂直である.
∴ AB ⊥ CD
又仮設によって AE ⊥ CD
依って CD は相交わる二直線 AB, AE の各に垂直であるから此の二直線の定める平面即ち三角形 ABE の平面に垂直である.
故に CD は三角形 ABE の平面上のすべての直線に垂直である.
∴ BE ⊥ CD
即ち本定理は証明せられた. ▪️
次に本定理の別証の一二を述べて見よう.
別証 1:
CD 上に E の両側に二点 F, G をとって EF = EG ならしめ BF = BG なることを証明して二等辺三角形の性質から BE が CD に垂直であることを結論しよう.
△AGF に於て
AE ⊥ GF (仮設)
EG = EF (作図)
故に △AGF は二等辺三角形となって
AG = AF
である.
従って直角三角形 ABG と ABF に於て AB は共通で AG = AF であるから
△ ABG ≡ △ ABF ∴ BG = BF
故に △BGF は二等辺三角形で BE はその頂点と底辺 FG の中点 E とを結ぶ直線となり
BE ⊥ GF ∴ BE ⊥ CD ▪️
別証 2:
CD 上に E の他に任意の一点 K を取り
なることを証明して「ピタゴラス」の定理の逆によって BE が CD に垂直なることを証明しよう.
CD 上に E の他に一点 K を取って AK, BK を結ぶと, AB は P に垂直であるから
∠ABK = ∠R
故に △AKB に於て「ピタゴラス」の定理により
又 △AKE も直角三角形であるから
故に上の両式から
∴
ところが AB は平面 P に垂直であるから
∠ABE = ∠R
故に △ABE において
∴
即ち △BEK の一辺 BK 上の正方形が他のニ辺上の正方形の和に等しいことになるから BK に対する角は直角である.
∴ BE ⊥ EM
∴ BE ⊥ CD
依って本定理は証明せられた. ▪️
次に
AB ⊥ P, BE ⊥ CD
なるとき, AE ⊥ CD なることを証明して見よう. 之は上の定理即ち三垂線の定理の逆ではあるが, これも矢張り三垂線の定理ということがある.
証明: AB⊥P (仮設)
∴ AB ⊥ CD
又 BE ⊥ CD (仮設)
故に CD は AB と BE の定める平面に垂直である. 従って CD は AB と BE の定める平面上の直線 AE に垂直である.
即ち
系 1. 平面 P 外の一点 A からこの平面に垂線 AB を引き, 其の足 B より P 上の直線 CD に垂線 BE を引けば, AE は CD の垂線である. ▪️
諸君は又三垂線の定理の別証 1, 2 に倣って此の系の別証を考えて見るがよい.
又三垂線の定理から次の事柄も容易に証明出来る.
系 2. 平面 (P) 外の一定 (A) からこの平面上の一直線 (CD) に垂線 (AE) を引き, その足 (E) を通りその直線 (CD) に垂線 (EB) をその平面内に引き, この垂線に始めの点 (A) より垂線 (AB) を引くときは, その垂線 (AB) は平面 P に垂直である.
証明:
AE ⊥ CD (仮設) BE ⊥ CD (仮設)
故に CD は AE と BE の定める平面即ち △ABE の平面に垂直である. 従って CD はこの平面上の直線 AB に垂直である.
依って AB ⊥ CD, AB ⊥ BE (仮設)
故に AB は CD と BE の定める平面即ち平面 P に垂直である. ▪️
ここで序でに系 2 を用いると容易に出来, しかも重要な作図題に就て研究しよう.
作図題 1. 一平面 (P) 外の一点 (A) より此の平面に垂線を引け.
作図:上に述べた系 2 と全く同じように作図する.
吟味:
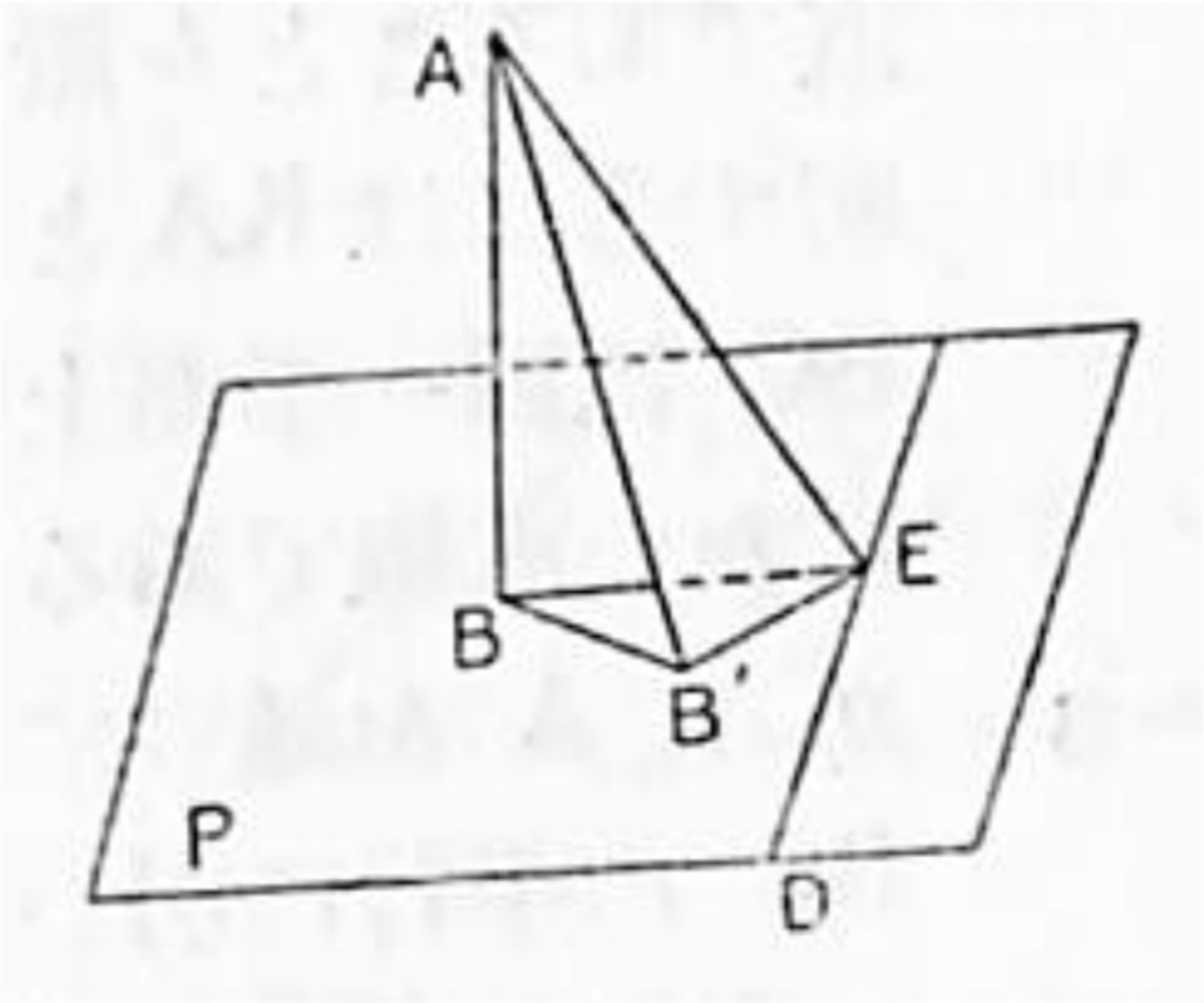
ここで問題になるのは A から平面 P に引いた垂線 AB が唯一つしかないことである. 平面 (P) 外の一点 (A) からこの平面に垂直な直線が AB, AB' の二本引けると仮定しよう. A から P 上の直線 CD に垂線 AE を引き BE, B'E を結ぶと三垂線の定理によって BE ⊥ CD, B'E ⊥CD.
依って平面幾何学の垂線の定理に反する. 故に A より平面 P への垂線は唯一つしかない.
或は又この場合 AB, A'B' の定める平面と P 平面との交線 BB' を考えると垂線の定義から
AB ⊥ BB', AB' ⊥ BB'
となるから AB, AB' の平面上で A から直線 BB' に垂直な直線が二つ引けることは矛盾であることを述べてもよい.
作図題 2. 一平面 (P) 上の一点 (A) を通り此の平面に垂線を引け.
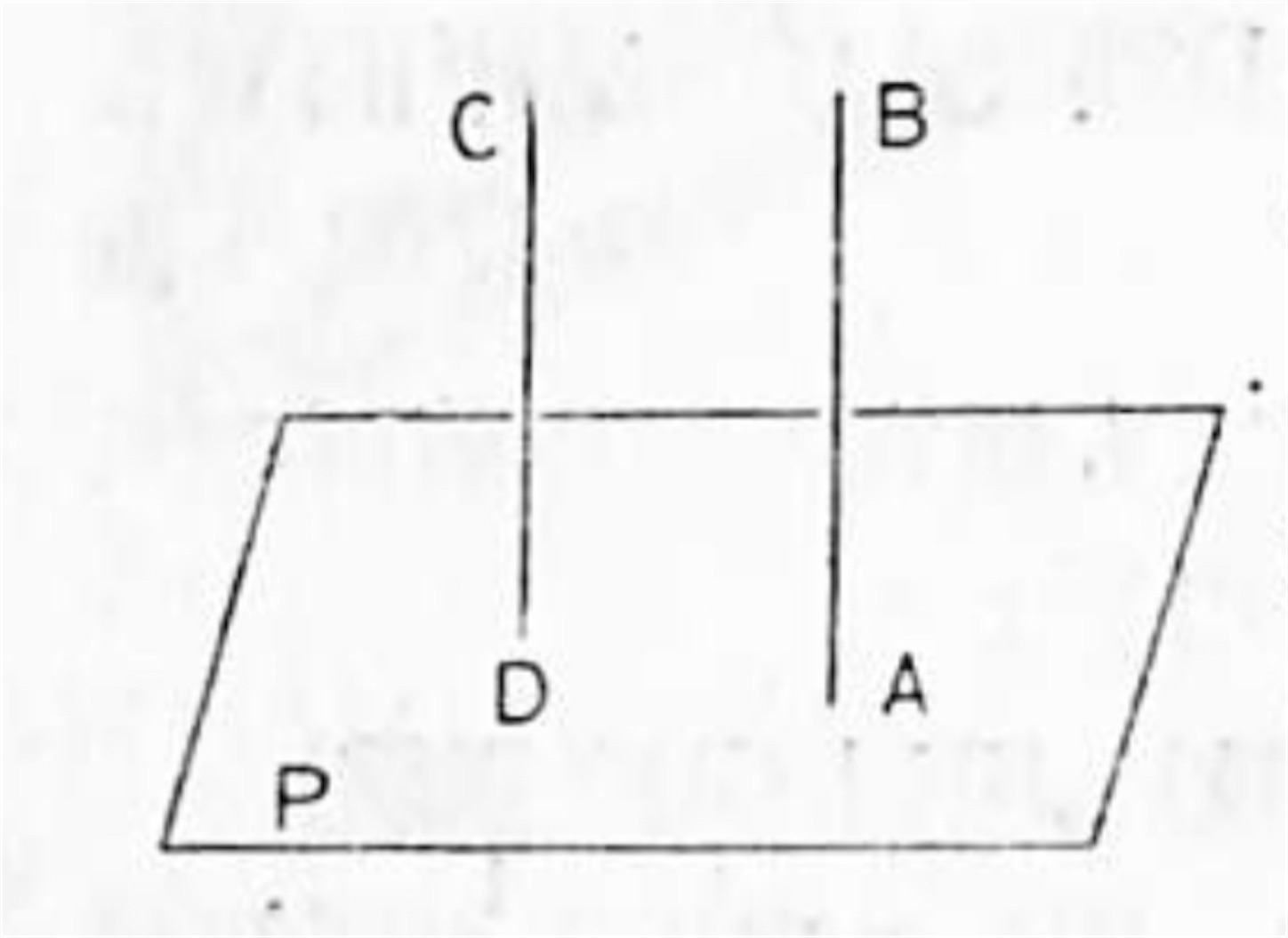
作図:P 外に任意の一点 C を取り, C より前の作図題を用いて P への垂線 CD を引く. 次に A より CD に平行に AB を引けばよい.
吟味: A を通る P の垂線は唯一つしかない. その証明法は前の作図題の吟味のところで述べた後の方法を用いるが便利である.
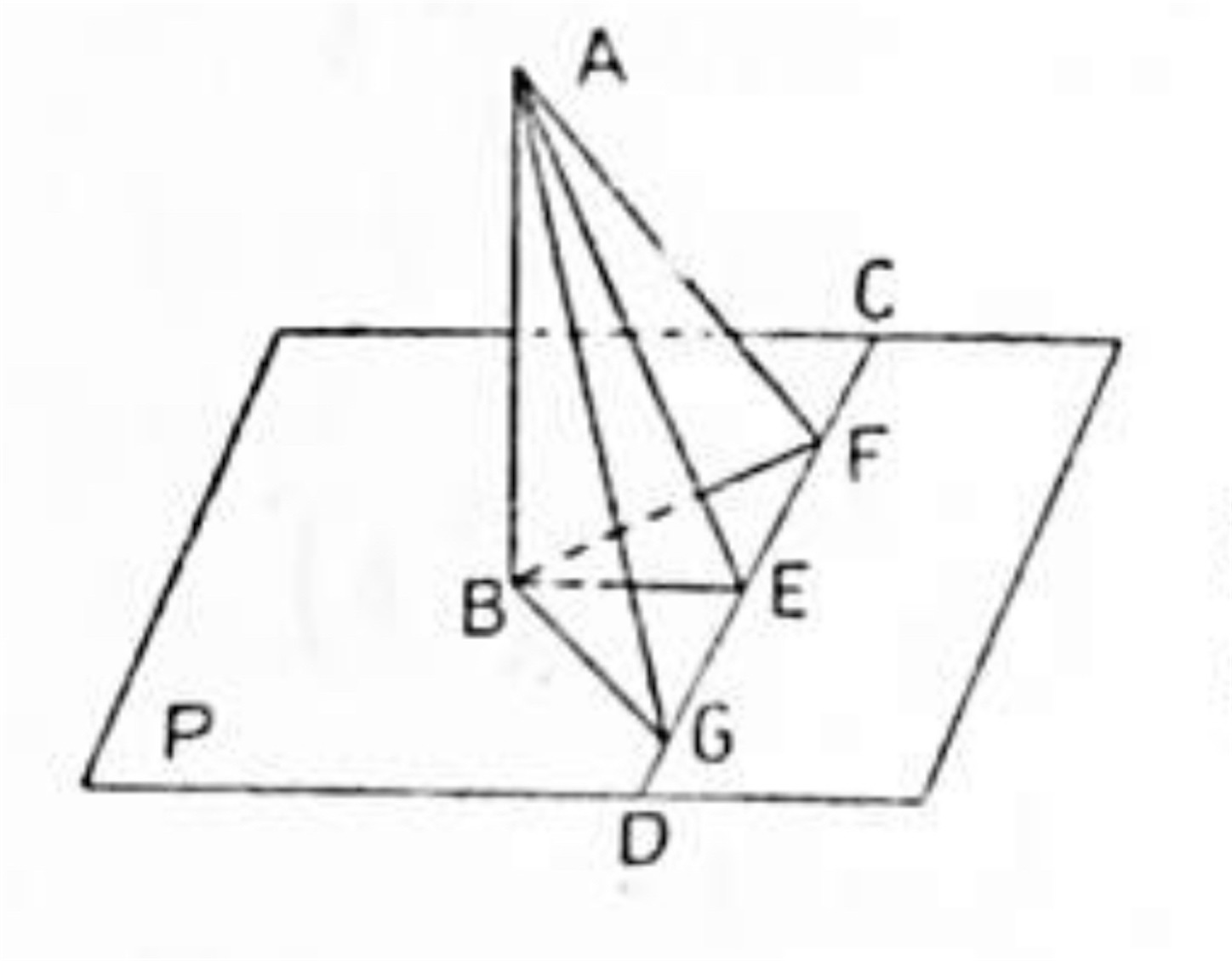
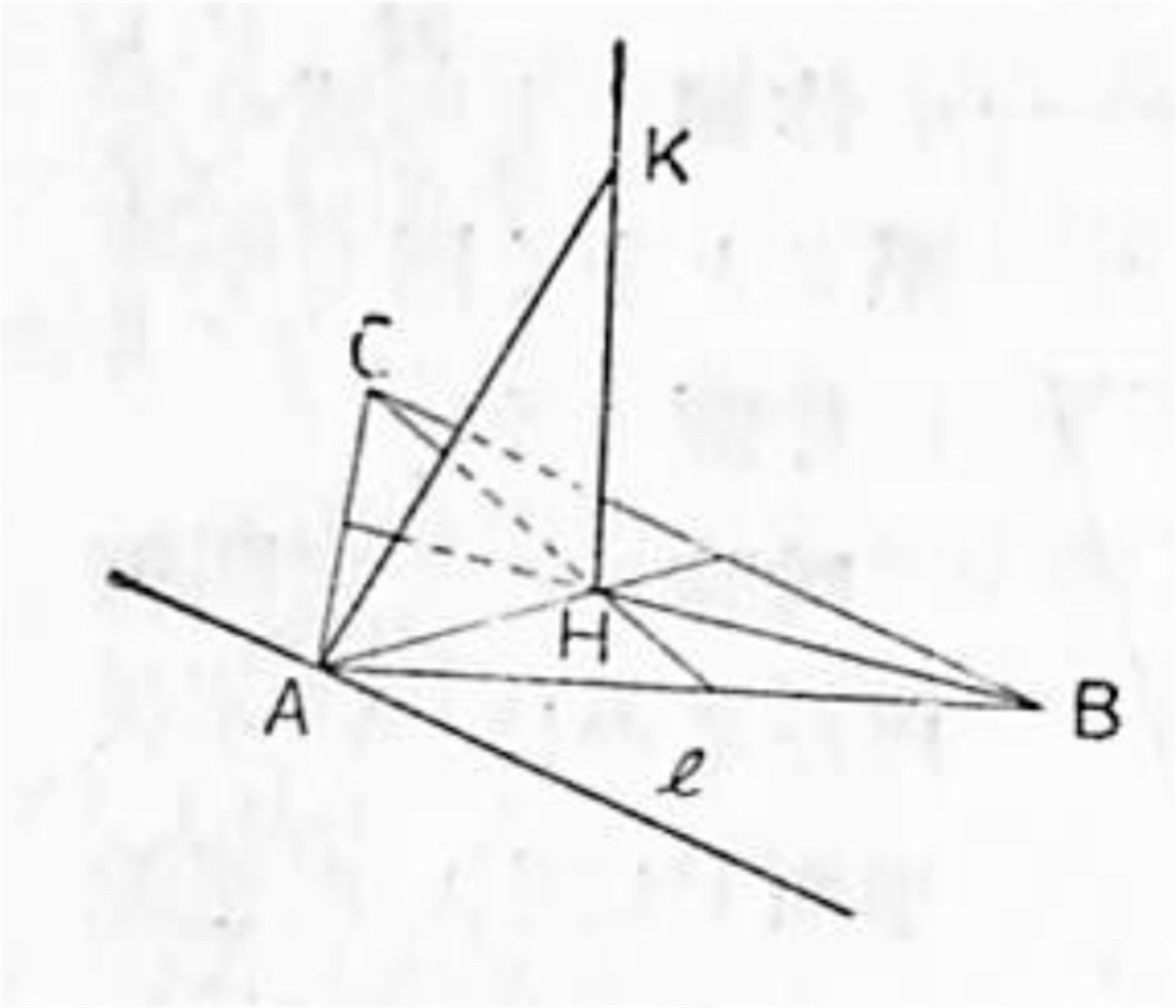
例題 三角形 ABC の垂心 H に於てこの三角形の平面に立てた垂線上に, 任意の一点 K を取れば KA, KB, KC は夫々 BC, CA, AB に垂直である.
KA が BC に垂直であることを証明するには KA と BC は同一平面上にない直線であるから, A を通って BC に平行に引いた直線が KA に垂直なることを言えばよい.
証明:A を通って BC に平行な直線を とすれば, H は △ABC の垂心であるから
AH ⊥ BC 従って AH ⊥
又 KH は △ABC の平面に垂直で は此の平面上の直線であるから前に述べた三垂線の定理の系 1 によって
KA ⊥
∴ KA ⊥ BC
全く同様にして KB ⊥ CA, KC ⊥ AB
即ちこれで証明された. ▪️
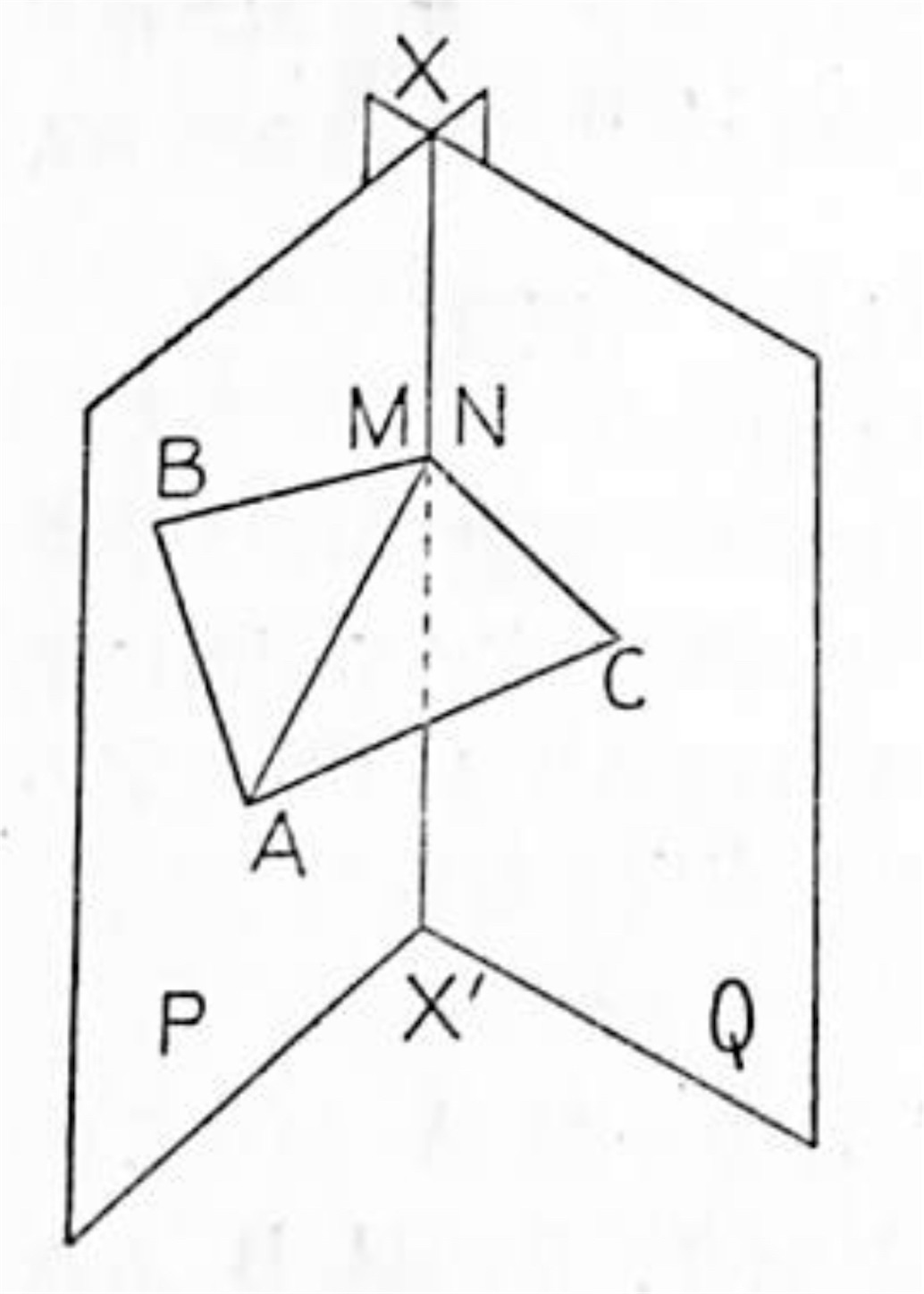
問題 1. 相交わる二平面 P, Q の何れの上にもない一点 A から, 各平面へ夫々垂線 AB, AC を引き, その足から二平面の交線 XX' へ夫々垂線 BM, CN を引けば, その足 M, N は一致することを証明せよ.
解:B, C から二平面 P, Q の交線 XX' に引いた垂線の足 M, N が一致することを証明するには平面 P 外の一点 A から P に垂線 AB を引き, B より XX' に垂線 BM を引いて CM を結び CM が XX' に垂直であることを言えばよい.
今 Q 平面を頭に置かないで MA を結んで見ると矢張り三垂線の定理の系 1 によって
AM ⊥ XX'
次に Q 平面に於て三垂線の定理を適用し
CM ⊥ XX'
依って題意の通りである. ▪️
尚又前問の証明を見るとわかるように
BM ⊥ XX', AM ⊥ XX', CM ⊥ XX'
である. 従って BM, AM, CM は何も M に於て二平面 P, Q の交線 XX' に垂直な平面上にある. そして AB, AC もその平面上にあることになる. そこでこの関係は次のような問題の形として言い表される.
問題 2. 一つの点から相交わる二平面の各に引いた垂線と, 二平面の交りに引いた垂線とは此の交りに垂直な同一平面上にある.
上に述べたように前問の図で AB, AM, AC が同一平面上にあって而もその平面は二平面 P, Q の交り XX' に垂直であることを言えばよい.
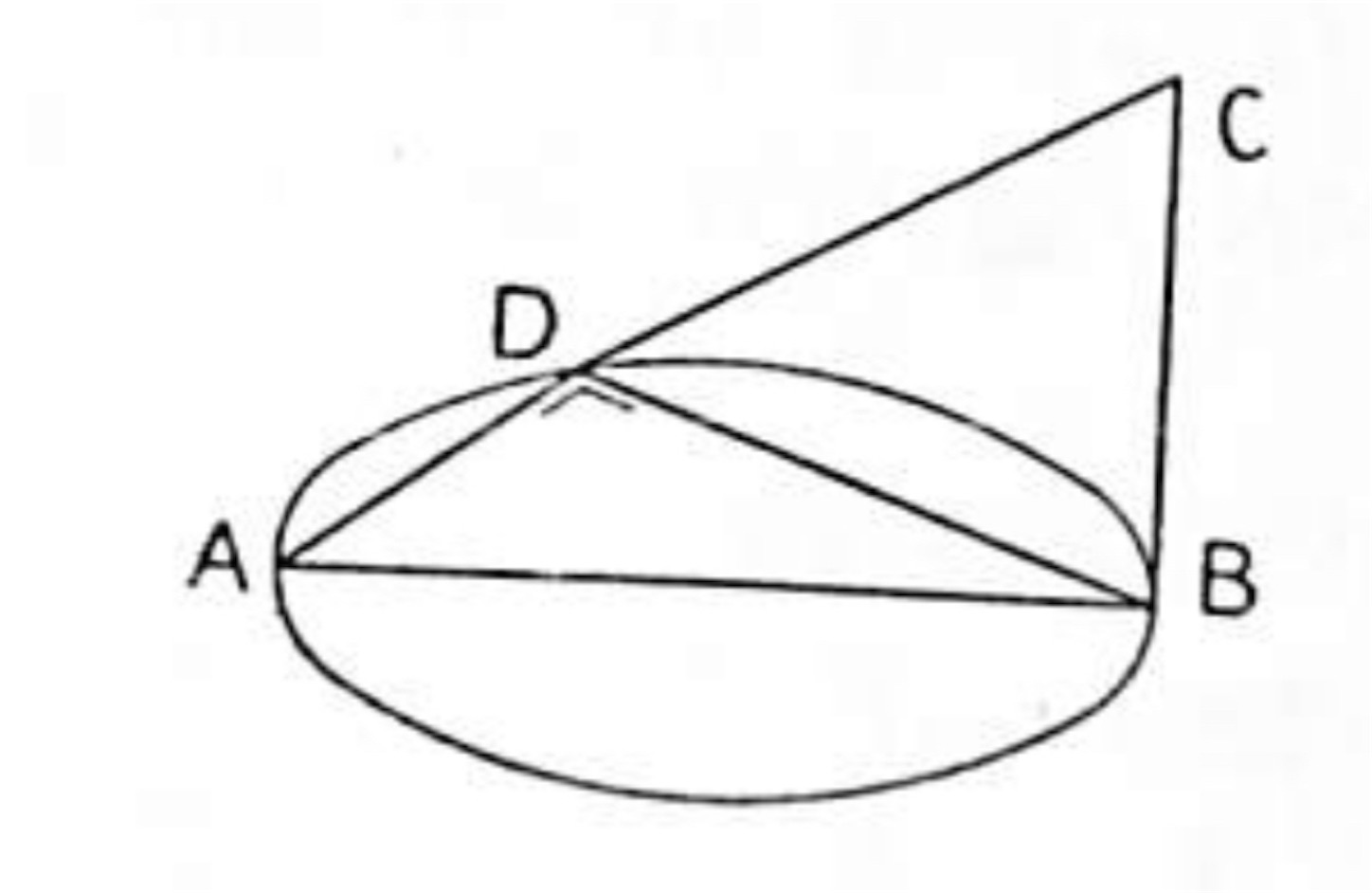
問題 3. 円の直径 AB の一端 B から此の円の平面に立てた垂線上に一点 C をとり, 又円周上に任意の一点 D をとれば, ∠ADC は直角である.
解:題意に従って図を書くと下の図のようになる.
この図で CB は円の平面に垂直で D が円周上の一点なるとき AD と CD が垂直であることを証明すればよい.
AB は円の直径で D は円周上の一点であるから平面幾何学の定理によって AD ⊥ BD である. 故に本問は次のように言い換えられる.
「一平面の垂線 (CB) の足 (B) より此の平面上の直線 (AD) へ垂線 (BD) を引くときは, その足 (D) と第一垂線 (CB) 上の一点 (C) とを結ぶ直線 (CD) は此の平面上の直線 (AD) に垂直である.」
即ち三垂線の定理系 1 と同題である. 故にくどく述べる必要もなく明らかである.
問題 4. AB を直径とする半円周の上に一点 D をとり, B より半円周の平面に垂線 BC を引き BC = AD とすれば, △CAB ≡ △CAD なることを証明せよ.
解:AD = BC なるものとして前問の図を代用しよう. 前問で証明したように CD ⊥ AD である. 故に AC を結ぶと △CAB, △CAD は何れも直角三角形で斜辺 AC は共通で他の一辺 BC と AD は仮設により相等しい.
∴ △CAB ≡ △CAD
問題 5. 垂直でもなく平行でもない二平面 P, Q の交線を XY とし, P 平面上の任意の一点から交線 XY 及び Q 平面に夫々垂線 AB, AA' を引き, 交線 XY 上の B 以外の任意の一点を C とすれば,
∠ABA' > ∠ACA'
である.
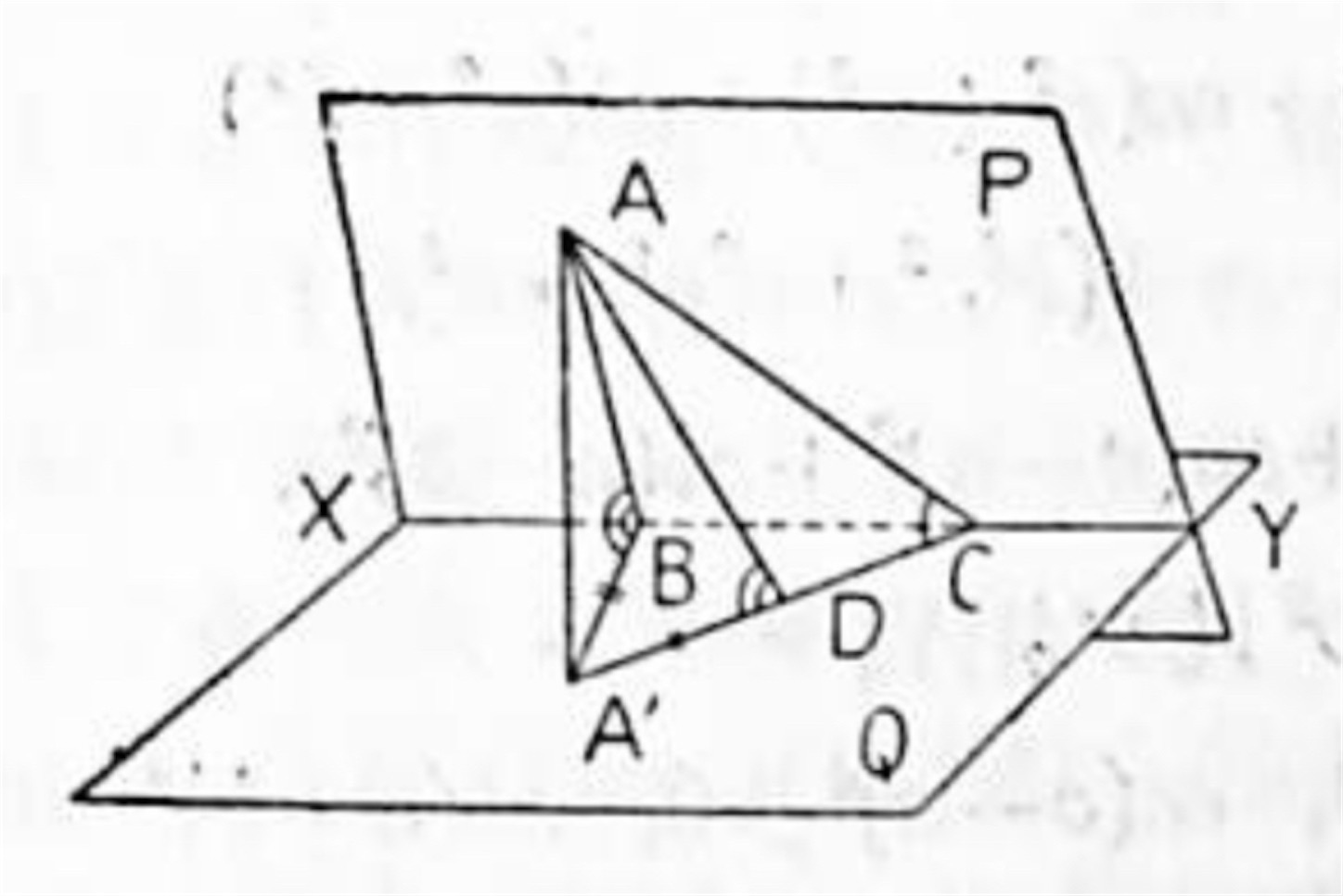
解:P, Q 二平面は XY で交わって垂直でない. 題意によって AB ⊥ XY, AA' ⊥ Q そして A は P 上の任意の一点であるから AB は P 上にあるし, A' は Q 上の点で B は交線 XY 上の点であるから A'B は勿論 Q 上の直線である.
依って今 Q 平面のみ注目すると
AA' ⊥ Q, AB ⊥ XY であるから
A'B ⊥ XY (三垂線の定理)
故に △BA'C は直角三角形となり
A'C > A'B
そこで A'C 上で A'B に等しく A'D をとると
∠ AA'B = ∠AA'D = ∠R
なる関係より
△ AA'B ≡ △ ADA' (二辺と夾角)
∴ ∠ ABA' = ∠ADA'
然して三角形 ADC を考えると
∠ ADA' > ∠ACA'
∴ ∠ ABA' > ∠ACA'