アセビ。
三諸者 人之守山 本邊者 馬酔木花開 末邊方 椿花開 浦妙 山曽 泣兒守山
三諸 (みもろ) は人の守 (も) る山、本邊 (もとべ) は馬酔木 (あしび) 花咲き、末邊 (すえべ) は椿花咲く、うらぐはし山そ、泣く兒 (こ) 守 (も) る山
作者: 不明

オオアラセイトウ (ムラサキハナナ) が咲き始めた。

ハナサフラン (クロッカス)。

サンシュユは満開。

シュンランが咲き始めた。

(143)(144)(145) の続き.
直線と平面の平行
既に一直線と一平面との位置関係には
(1) 相交わる場合
(2) 直線が平面に含まれる場合
(3) 平行なる場合
の三つの場合があることを研究した. 次に直線と平面が平行となる場合の重要な事項を研究して見よう.
I.
定理 一つの直線が一つの平面に平行なるときには, その直線を含む任意の平面と前の平面との交線はその直線に平行である.
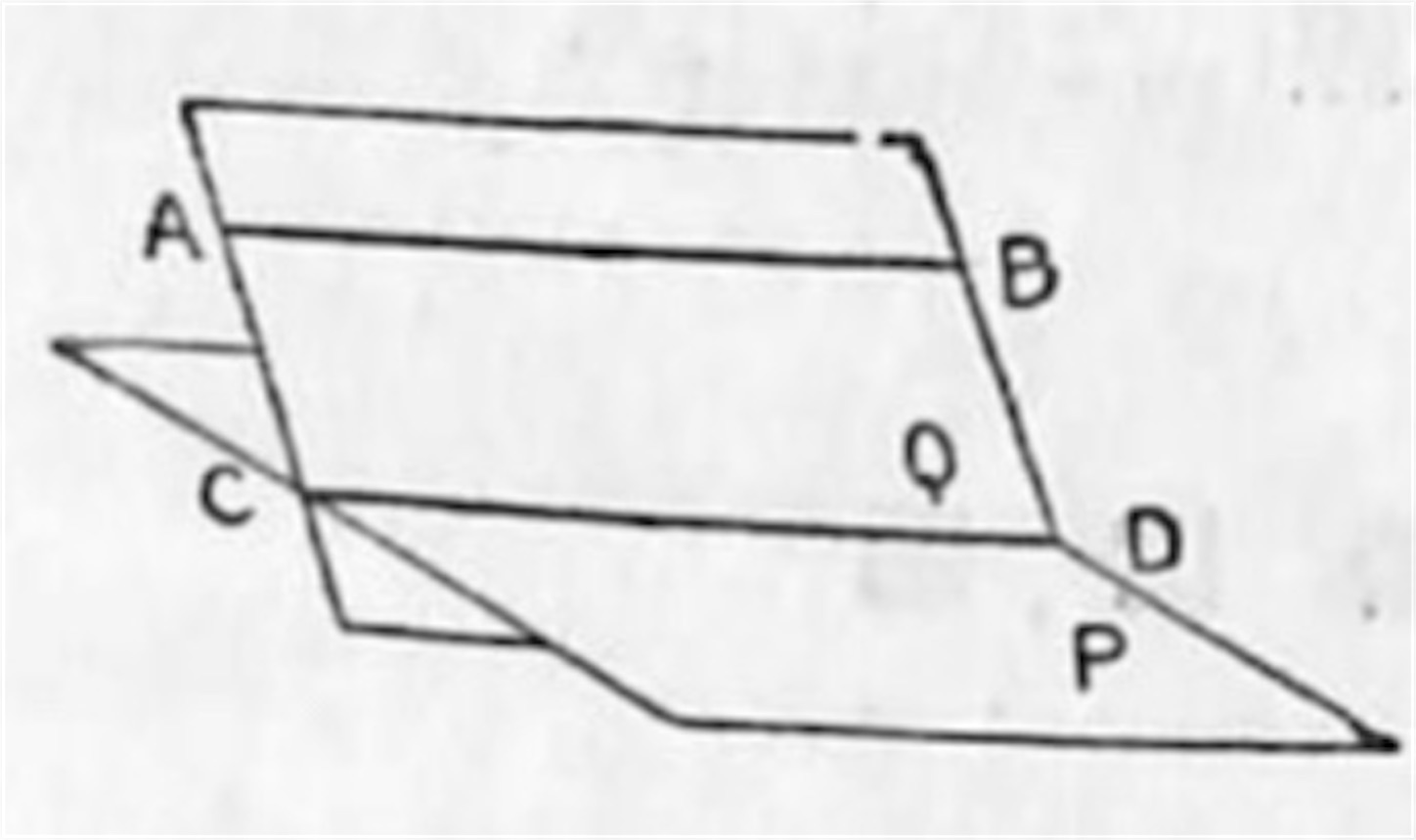
証明:直線 AB と平面 P があってこれが平行なるとき, AB を含んで P と交わる任意の平面 Q を作り, P と Q との交線を CD と名づけるとき AB ‖ CD なることを証明するのが題意である. AB ‖ CD を証明するには AB と CD が同一平面上にあること, 出会わないことの二つを証明せねばならない.
題意によって AB ‖ P であるから AB と P 上の直線 CD とは出会わない. そして AB と CD とは同一平面 Q 上にある.
∴ AB ‖ CD
即ち此の定理は証明された. ▪️
[I] 次に一直線 AB が平面 P に平行なるとき, P 上の一点 C を通って AB に平行に引いた直線 CD と P の位置の関係をしらべよう.
AB と CD は平行であるから一平面を定める. それを Q とすると Q と P は一点 C を共有するから C を通る一直線 CD' で交わる.
故に上の定理によって
AB ‖ CD'
然るに C を通り AB に平行なる直線は唯一つしかないから CD と CD' とは同一直線であるべきである. 依って CD は平面 P に含まれる. 即ち
平面上の一点を通って此の平面に平行な直線に平行に引いた直線は全く此の平面に含まれる.
[II] 次に又 AB に平行な二平面 P, Q が CD で交わるとき, CD と AB との関係はどうであるかを見よう.
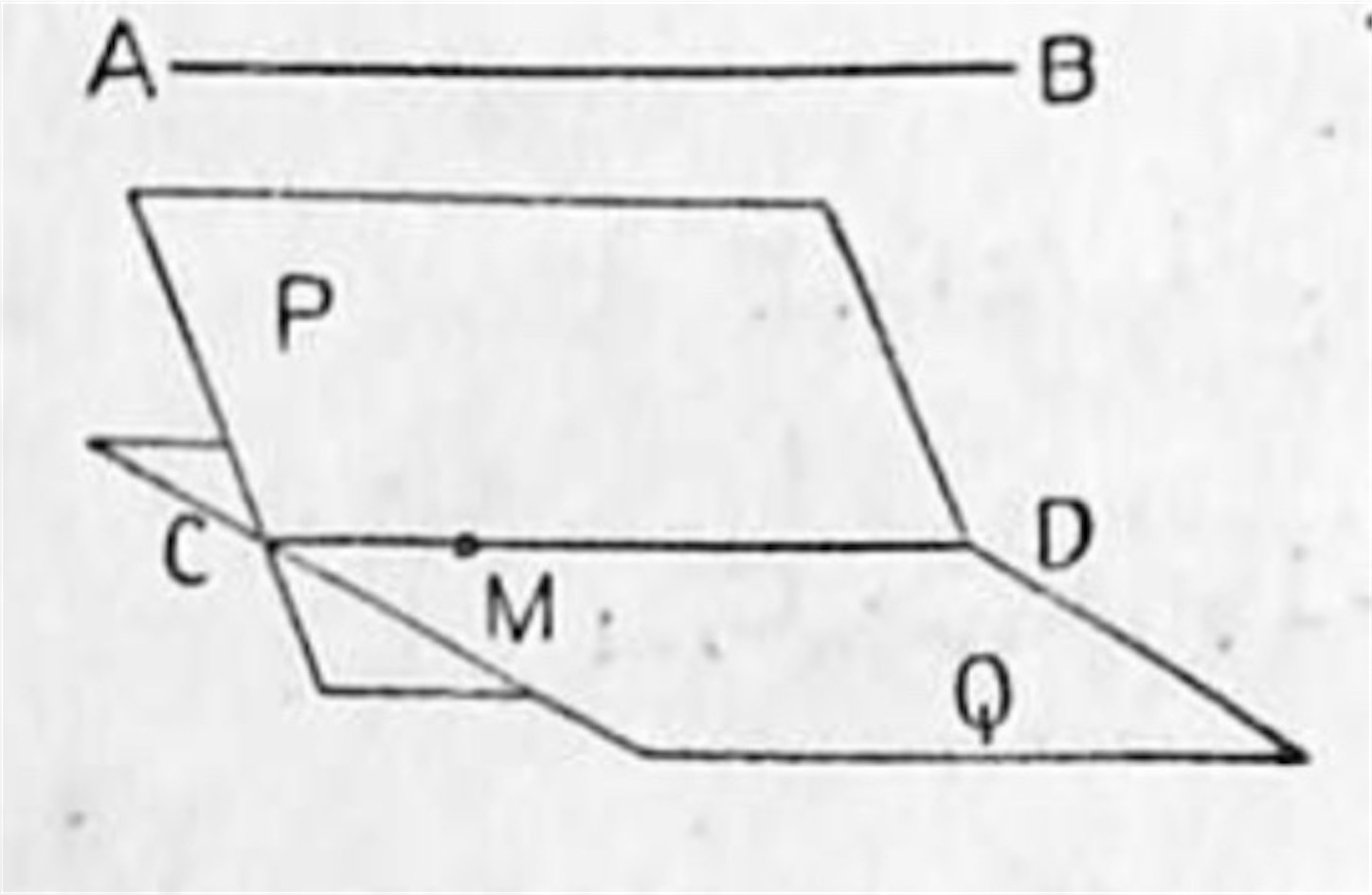
交線 CD の上の一点 M を通って AB に平行な直線 MN を引いて見れば, M は P, Q 二平面の共有点であるから MN は P, Q の何れにも含まれる. 故に MN は CD に一致する. 即ち
相交わる二平面が何れも同一の直線に平行なるときは, その交線も亦その直線に平行である.
II.
定理 二つの直線が平行なるときはその一方のみを含む平面は他の直線に平行である。
その一方のみを含むのであるから他方を含まないことは明らかでこの平面が他方の直線と平行であることは説明するまでもないと考えるかもしれない。然し平面が他方の直線を含まないことは明瞭であっても直ちに平面と直線とが平行であると断定するのは誤りである。相交わっているかも知れないからである。
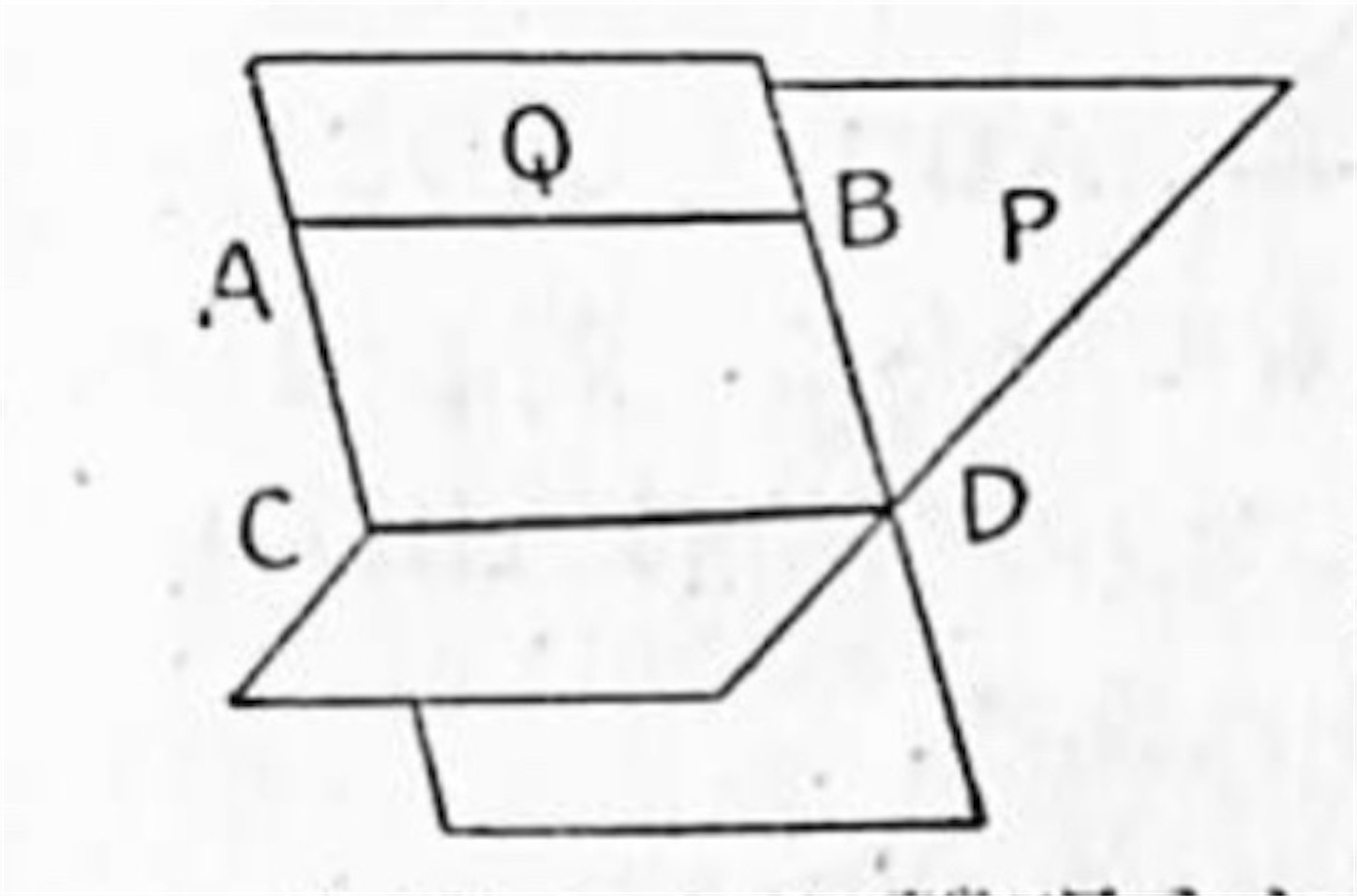
証明:二つの平行線 AB, CD があるとき P は CD を含み AB を含まない平面とすると AB は P と平行であることを証明すればよい。二つの平行線 AB, CD が定める平面を Q と名づけると直線 AB は Q に含まれているから若し此の直線が平面 P と交わるものとすれば、その交点は二平面 P, Q の交線なる CD 上の点でなければならぬ。然し AB は CD と平行であるから CD とは交わらない。故に平面 P とも交わらない。
∴ AB ‖ P ▪️
[I] 次に相交わる二平面 P, Q が平行二直線 AB, CD の各一つを含むとき, その交線 EF と AB, CD との関係はどうなるであろうか.
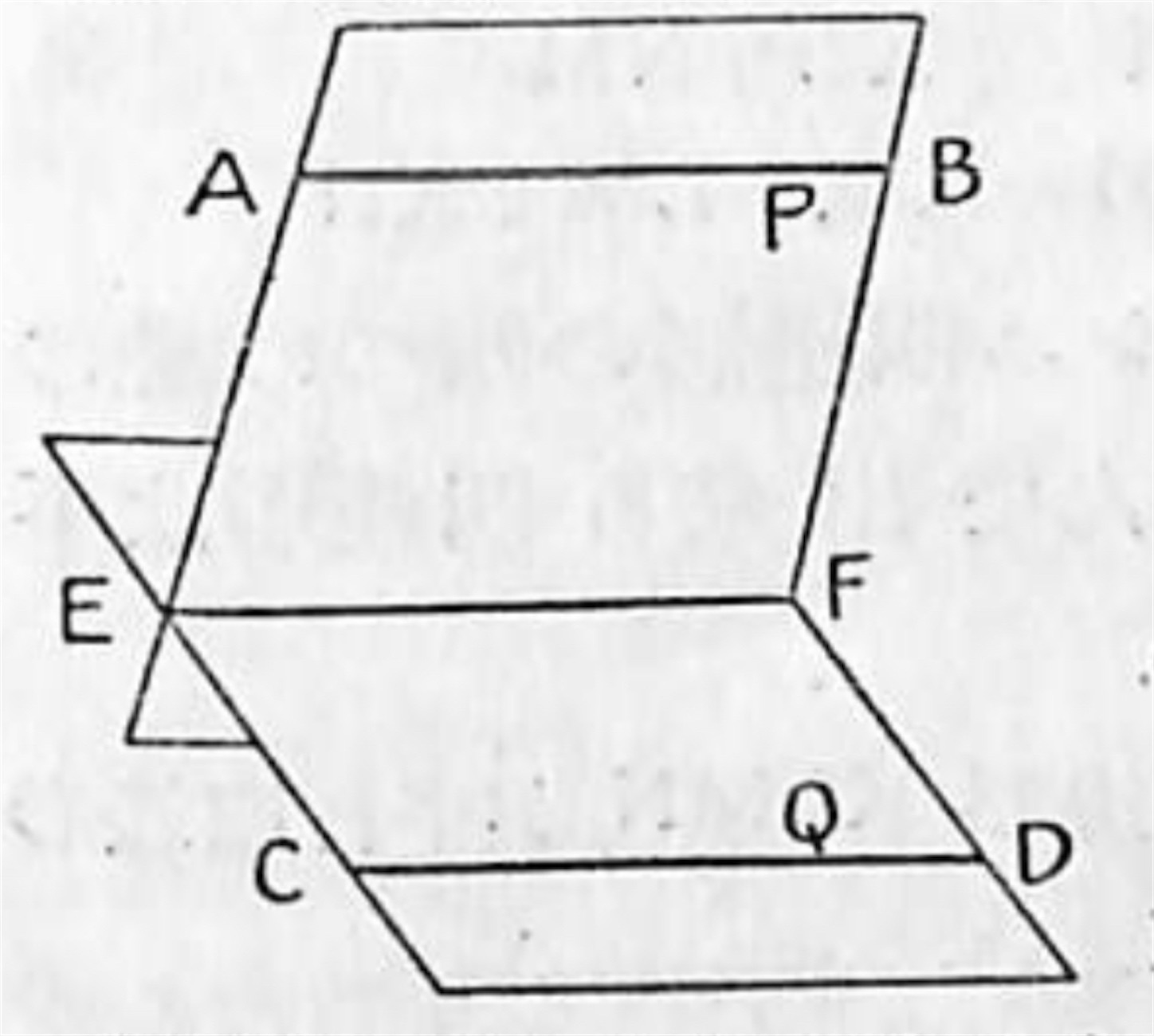
AB ‖ CD であるから上の定理によって AB ‖ Q, 依って AB は平面 Q 上の直線 EF とは交わらない。然して AB と EF とは同一平面 P 上にある。
∴ AB ‖ EF
同様に CD ‖ EF
即ち
平行な二直線の各一つを含む平面が交わるときは, その交線は二つの直線の各に平行である。
[II] 更に又 AB と CD が平行で且つ AB と EF とが平行なるとき CD と EF との関係を調べよう.
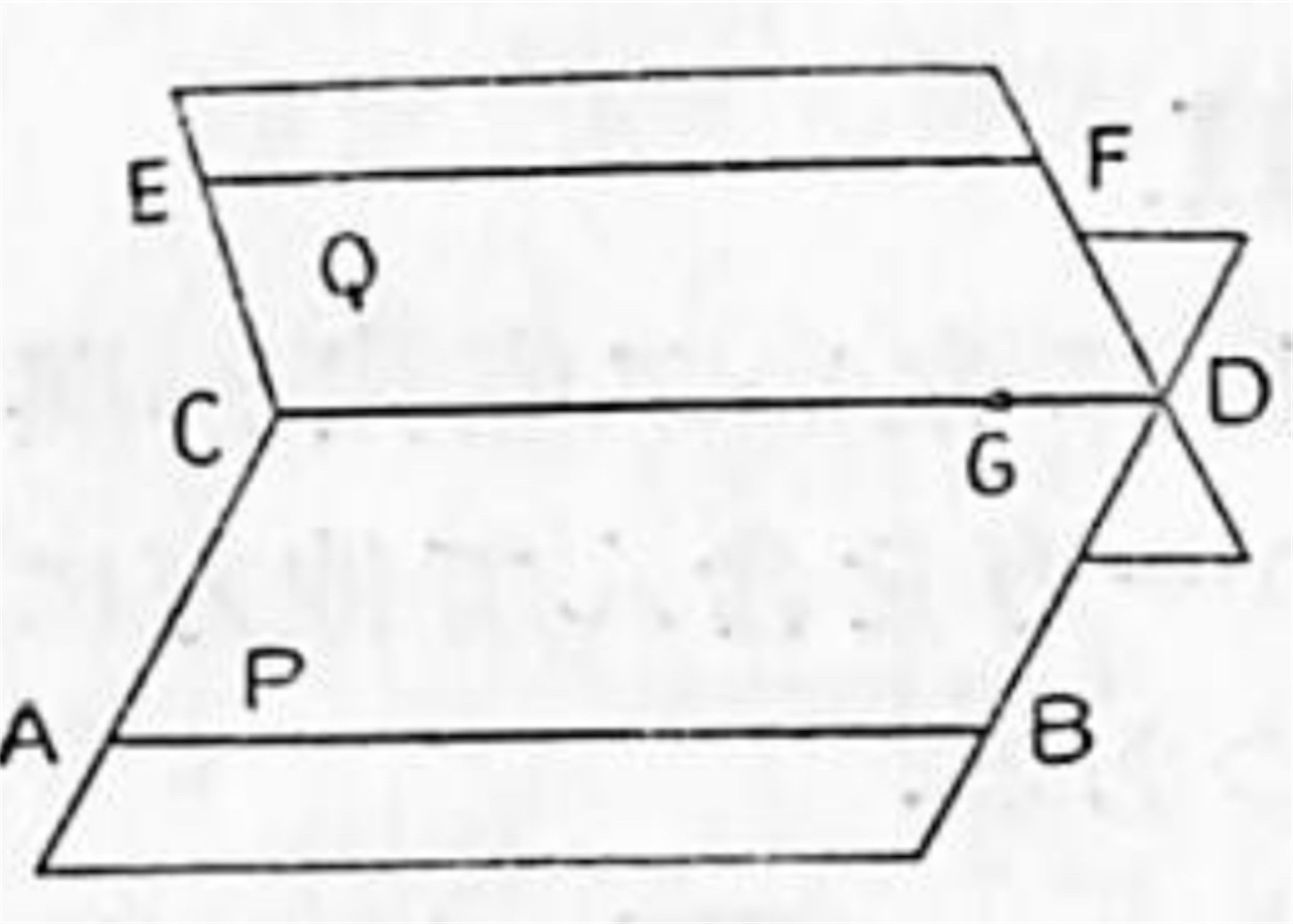
EF が AB と CD の定める平面上にあるときは平面幾何学で学んでいるように
CD ‖ EF
である. EF が AB と CD の定める平面 P に含まれない場合には EF と CD 上の一点 G との定める平面 Q を考えると [I] の研究によって P と Q との交線は AB に平行である. 故にその交線は P 上にあって AB に平行で且つ G を通るから CD に一致せねばならない.
従って CD は平行直線 AB, EF の各を含む二平面 P, Q の交線となるから [I] によって EF に平行である. この結果は次のように述べてよい.
同一の直線に平行な二つの直線は互に平行である。
[III] 尚進んで AB と CD が平行なるとき, AB に平行な平面 P と CD の関係を研究しよう.
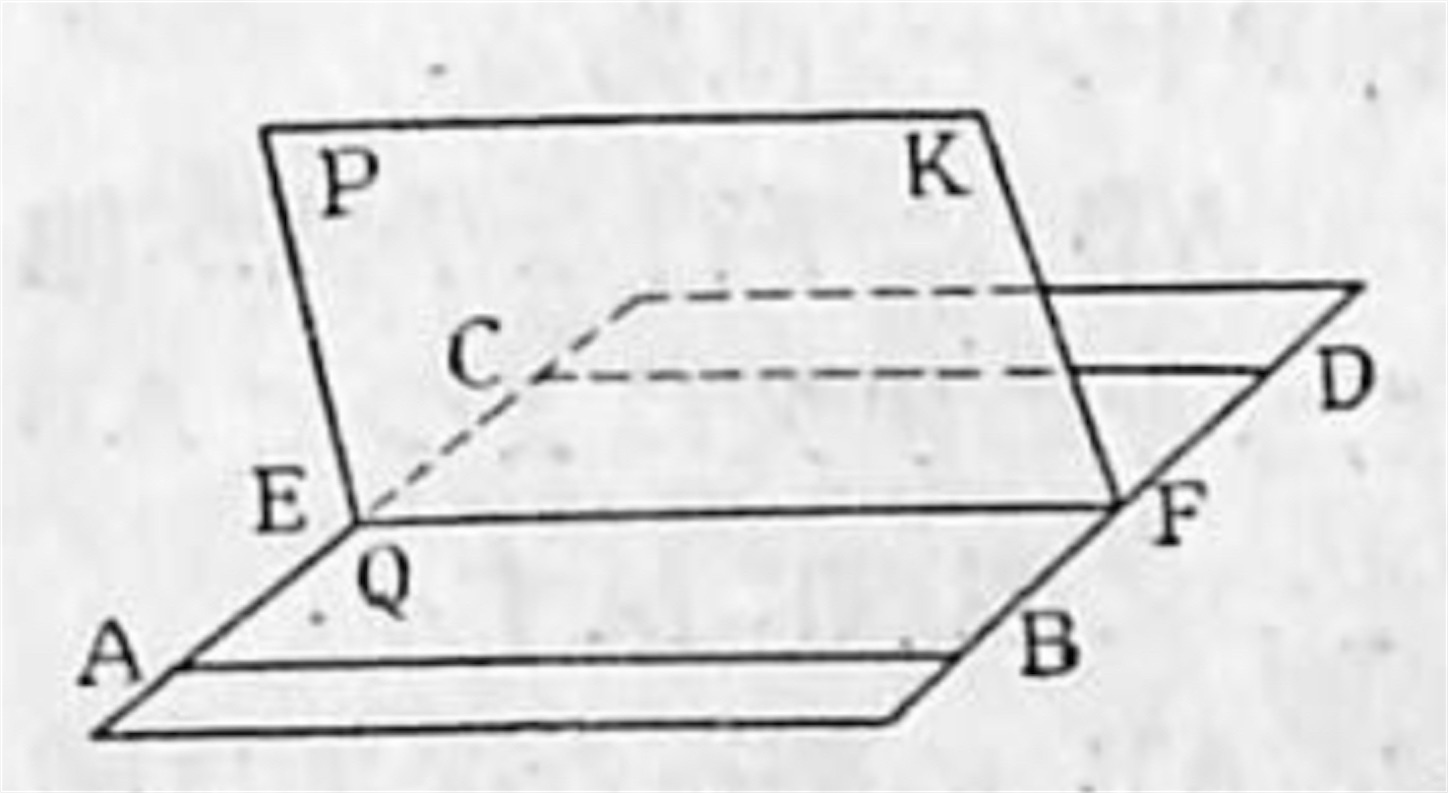
P とCD とが一点 C を共有すればさきに述べたことによって CD は P に含まれる.
次に AB, CD の定める平面 Q 上に於て AB に平行な直線を EF とし, 又 Q 外の一点を K とすれば EF と K の定める平面 P は AB に平行である.
而して EF は CD にも平行であるから P は又 CD にも平行である.
故に AB に平行なる平面 P は CD を含むか, 或は CD に平行となって CD にまることはない.
即ち次の様に述べてよい.
二つの平行線の一方に平行な平面は他の線とは交わらない. 然して他の線を含むか或いは平行である.
III.
例題 同一平面上にない二直線が与えられたとき, その一方を含んで他方に平行な平面は唯一つある.
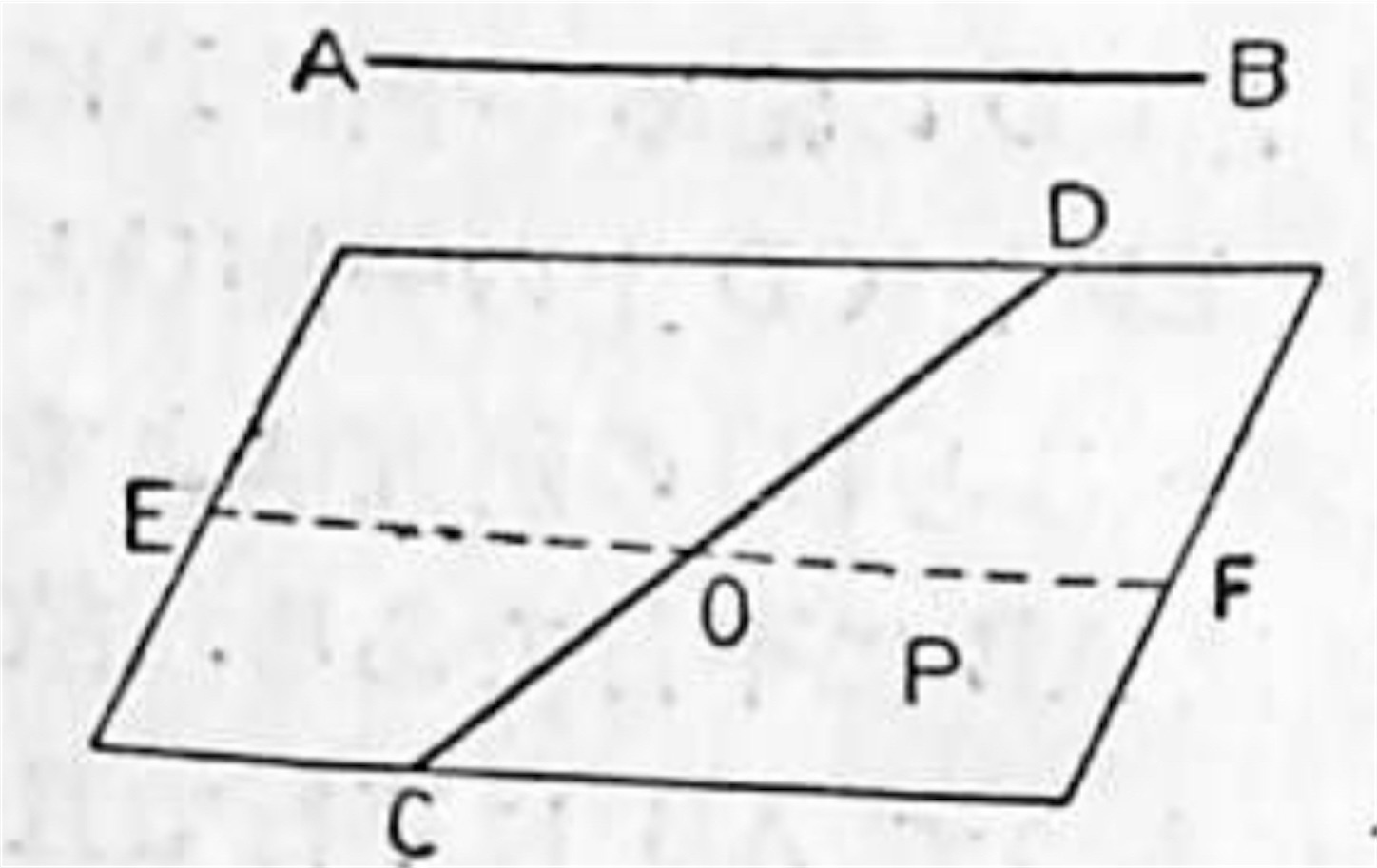
証明:AB, CD を同一平面上にない二直線とするとき, CD を含んで AB に平行な平面 P は唯一つあることを証明せよ, というのが題意である.
CD 上の一点 O と AB の定める平面上に於て, O を通り AB に平行な直線 EF を引くときは, 二直線 CD, EF の定める平面 P は AB を含まない. 何となれば P が AB を含む とすれば AB, CD が同一平面にあることになって仮定に反するからである.
故に P は平行線 AB, EF の一方 EF のみを含むから AB に平行である. 即ち CD を含み AB に平行な平面 P は一つはある.
次に CD を含んで AB に平行な平面が他にあると仮定すれば, さきの研究によって AB と CD とが平行となって仮設に反する.
依って CD を含み AB に平行な平面は唯一つあるのみである. ▪️
此の例題は又次の軌跡問題として改めて掲げることも出来る.
同一平面中に無い二直線 AB, CD が与えられたとき, AB に平行で CD に交わる直線の軌跡は, CD を含んで AB に平行な平面である.
問題 1. ゴーシュ四辺形 ABCD の辺 AB, BC, CD, DA の中点を夫々 K, L, M, N とすれば
KL = NM, KL ‖ NM, LM = KN, LM ‖ KN である.
註:総ての辺が同一平面上にない多角形をゴーシュ (Gauche) 多角形又は空間多角形という. ゴーシュ四辺形 ABCD といえば対角線 AC が分ける二つの三角形 ABC と ADC とが別々の平面中にあるものである. 若し他の対角線 BD を考えると二つの三角形 ABD と BCD とが別々の平面中にある.
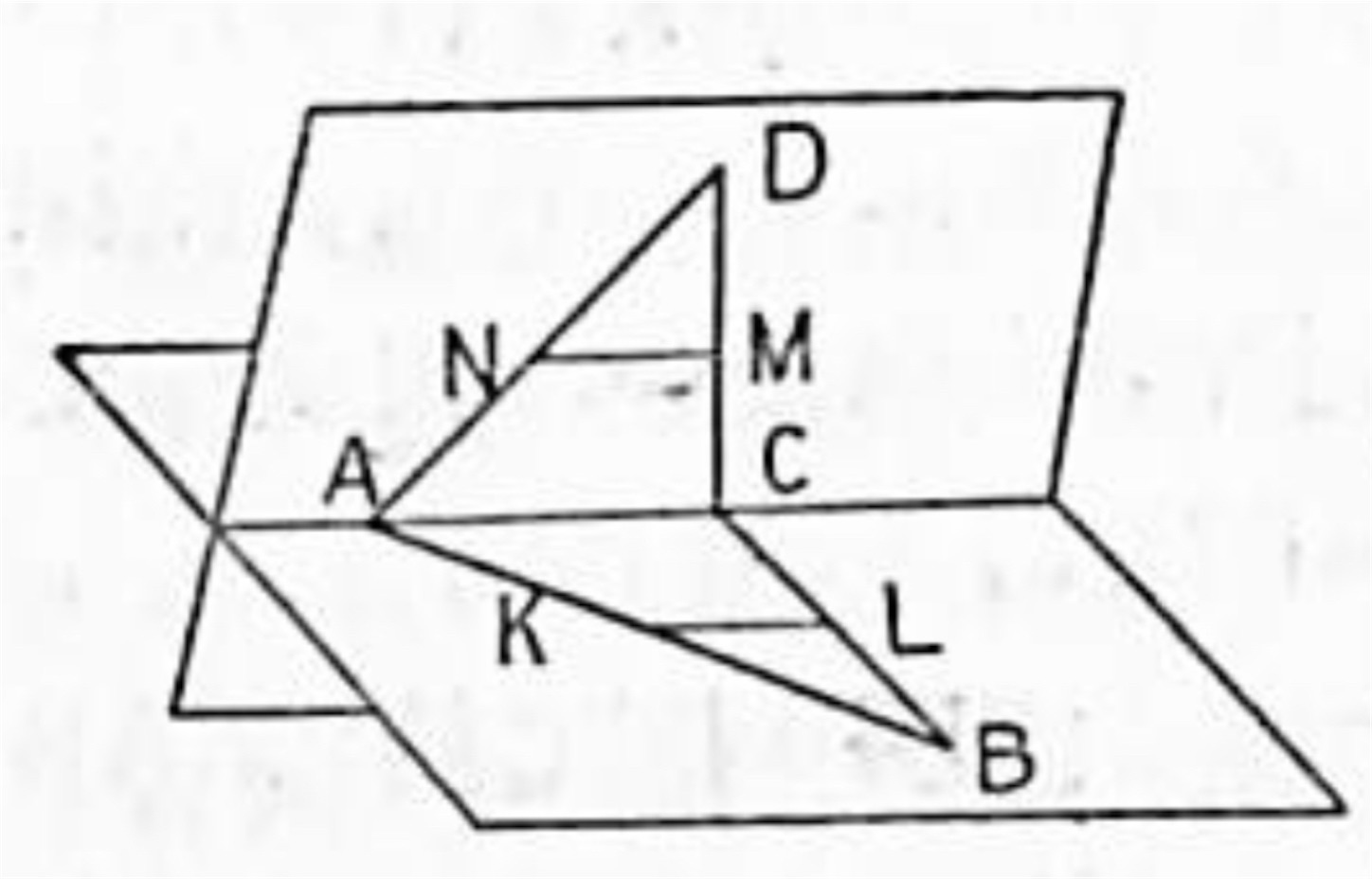
略解:図に於て K, L は夫々辺 AB, BC の中点であるから平面幾何で学んで定理「三角形の二辺の中点を結ぶ線分は第三辺に平行で且つその半分に等しい」により
従って,
同様にして
. ▪️
問題2. ゴーシュ四辺形の四つの辺の中点を順次に結ん で出来る四辺形は平行四辺形である.
上の図により四辺形 KLMN が平行四辺形なることをいえばよい.
問題 3. ゴーシュ四辺形の相対する点を結ぶ二つの線分は相交わり, 而も互に他を二等分する.
前問により四辺形 KLMN は平行四辺形であって MM, NL はその二つの対角線であるから相交わり且つ互いに他を二等分する.
問題 4. 一つの平面 P に平行なる一直線を含む任意の平面 (Q, R) 等と此の平面 P との交線 CD, EF 等は互いに平行である.
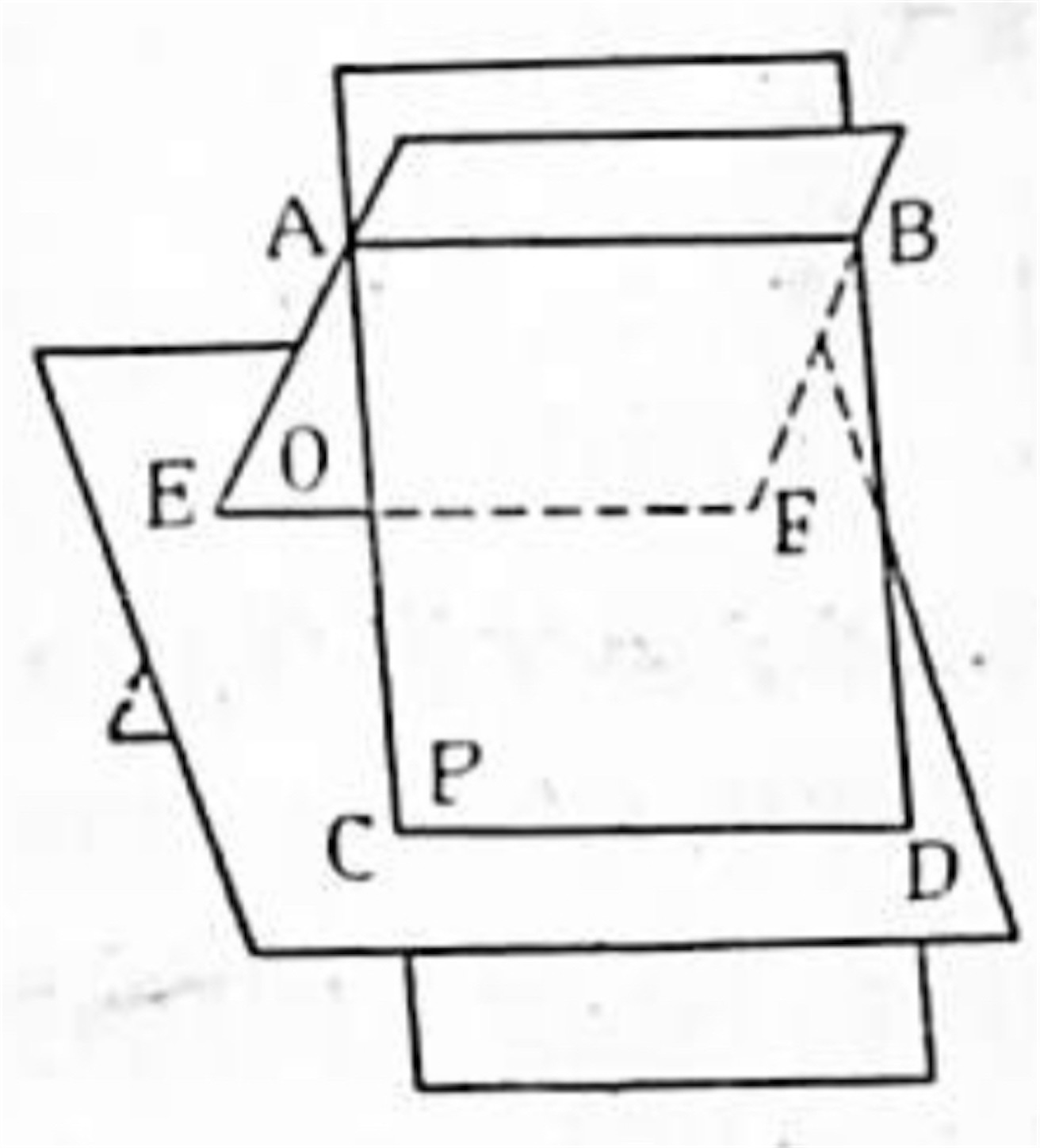
略解:AB は平面 P に平行で CD, EF 等は AB を含む任意の平面 Q, R 等と P の交線であるから定理によって
AB ‖ CD
AB ‖ EF
然して又同一直線に平行な直線は互いに平行であるから CD ‖ EF.
問題 5. 二平面 P, Q の交線 AB に平行な平面 R と P との交線を CD とし, R と Q との交線を EF とするときは EF ‖ CD なることを証明せよ.
各自図を書いて考えて見よ. 前問と全く一致することがわかる.
問題 6. 直線 AB が平面 P に交わるときは P 上には AB に平行なる直線は一つも引き得ないことを証明せよ.
略解:平面 P 上に AB に平行な直線 CD が引けたものと仮定すれば, P は (平行線 AB と CD の一方) CD と AB 上の一点を含む平面となる. 故に P は平行線 AB, CD の決定する平面で直線 AB を含むことになり仮設に反する. 故に P 上には AB に平行な直線は一つも引き得ない.
問題 7. 平行線 AB, CD の一つ AB に交る平面 P は又 CD にも交わることを証明せよ.
略解:AB と P との交点を M とすれば若し CD が P に平行だと仮定すれば, P 上の一点 M を通り CD に平行な直線 AB は P に含まれて仮定に反する.
又 CD が P に含まれると仮定すれば, 平行線 AB, CD の定める平面と P とは一直線 CD と M を共有するから一致し AB は P に含まれて又仮定に反する. 故に CD も亦 P に交わる.
問題 8. 与えられた平面 P 外の一点 M を通り P に平行な直線を引け.
略解:P 上に任意の直線 CD を引き, M と CD との定める平面内に於て M を通り CD に平行な直線を引けばよい. (無数に引ける.)
問題 9. 同一平面上にない二直線 AB, CD 外の一定点 M を通りその各に平行な平面を作れ.
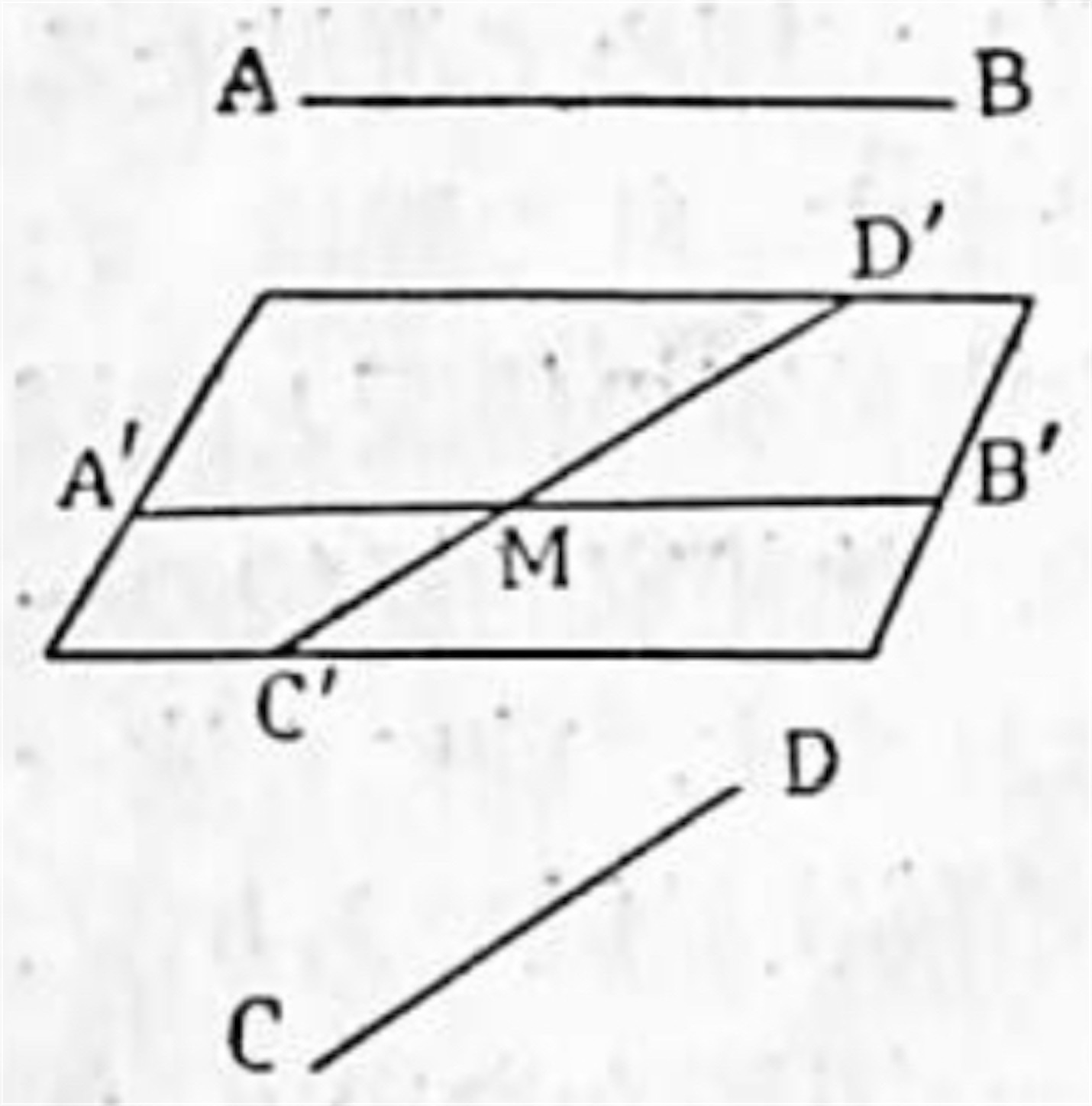
解析:求める平面 P が作図出来たと仮定すれば
AB ‖ P, CD ‖ P
である. 故に M を通り夫々 AB, CD に平行な直線 A'B', C'D' を引くと A'B', C'D' は共に P に含まれる. 故に P を作るには M を通り AB, CD に平行な直線 A'B', C'D' を引いてその二直線が定める平面を作ればよい.
作図:M とAB との定める平面を作りその平面上に於て M を通り AB に平行なる直線 A'B' を引く. 次に M と CD との定める平面上に於て M を通り CD に平行な直線 C'D' を引き, A'B' と C'D' の定める平面 P を作れば求めるものである.
証明:作図によって A'B' ‖ AB 故に AB が P に含まれなければ AB ‖ P. 同様に CD ‖ P.
吟味: AB, CD の中の何れか一方は A'B' と C'D' の定める平面 P に含まれることがあり得る. この場合はその直線と P とは平行とはいえない. 依って作図は不能である.