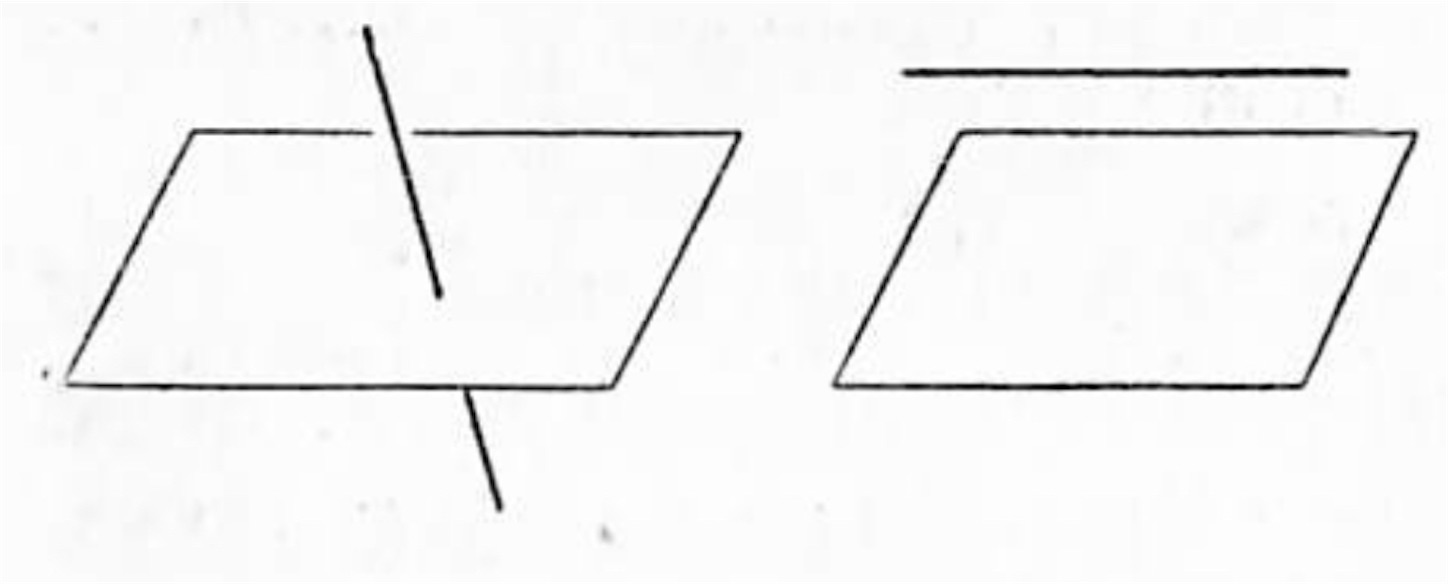前の記事の続き。
直線と平面
二つの直線の位置の関係
諸君は五月創刊号で平面が決定せられる種々の場合に就て詳しく学んだ。次に空間に於ける二つの直線の相互の位置関係に就て研究して見よう。
空間に於ける二つの直線の相互の位置関係は同一平面上にある場合とそうでない場合との二つに大別することができる。
同一平面上にある二直線は既に平面幾何で学んだように相交わるか平行なるかの何れかであって交わりもせず平行でもないような場合は起り得ない。
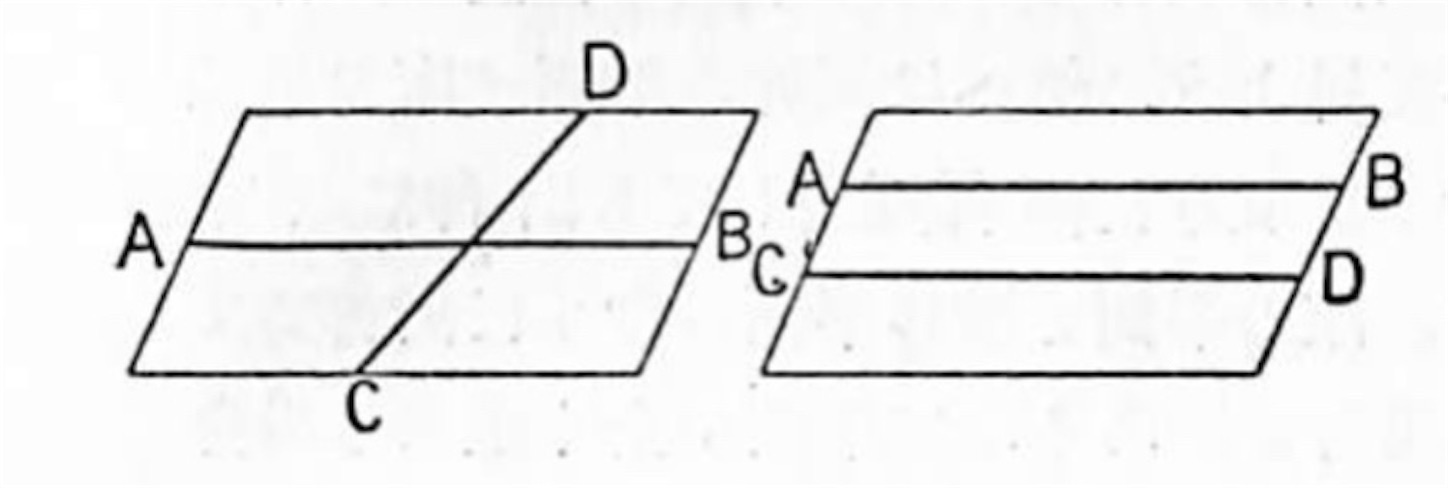
併し吾々は至る処で汽車道とその下を通る電車道、十字路に於て頭上を東西に通ずる電線と南北に通ずる電線、又例えば教室内では天井に左右に引かれた直線と床の上に之と異なる方向に引かれた直線等のように交わりもせず平行でもあり得ない二直線を見ることが出来る。かような二直線を「同一平面上にない二直線」又は「相交わらず且つ平行でもない二直線」というのである。
依って空間に於ける二直線の位置の関係は次のように分類せられる。
[l] 同一平面上にある場合
(1) 相交わる場合
(2) 平行なる場合
[II] 同一平面上にない場合
この場合は相交わらず又平行でもない場合である。
この [II] の場合はよく忘れ勝ちである。平面幾何学では二直線の平行なることを証明するにはそれが相交わらないことを証明すればよく、又反対に二直線が相交わることを証明するにはそれが平行でないことを証明すればよかった。併し立体幾何学では二直線の平行なることを証明するのに同一平面上にあることの証明を落として単に交わらないことの証明だけを述べたのでは不十分である。平行線ではなくて同一平面上にない二直線に過ぎない場合があるからである。
例題 1. 同一平面上にない二直線の双方に交わる二つの直線は平行とはならないことを証明せよ。
証明: 同一平面上にない二直線を a, b とし、a, b の双方に交わる二直線を c, d とする。今 c, d が平行 であると仮定すれば此の二直線は一平面を決定する。この平面を P とするとき、a, b は c にも d にも交わっているから P 上の二点を通る直線である。故に共に P に含まれる。然しこれは仮設に反する。依って c と d は平行にはなり得ない。
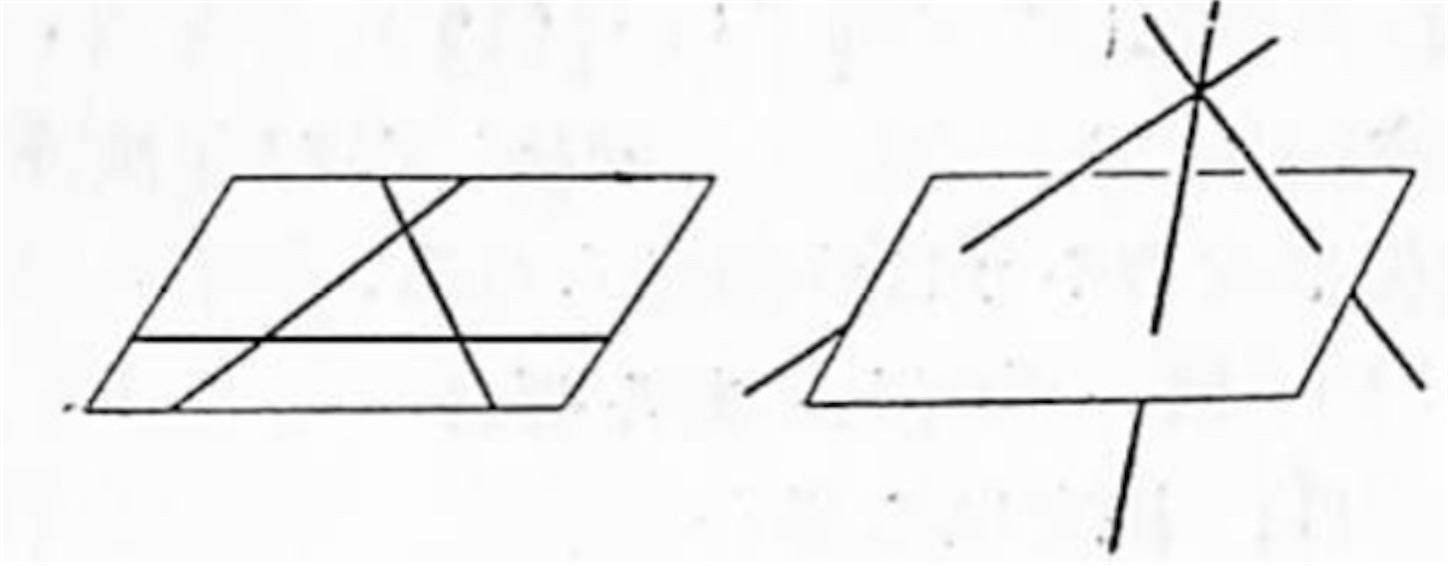
問題 1. 二つ宛相交わる三つの直線の位置の関係を説明せよ。
先づ相交わる二直線を考え、次に此の両方に交わる第三の直線を考えると、初めの二直線の交点を通らない場合は三角形を作って同一平面上にあることになり、初めの二直線の交点を通れば同一点を通る三直線となって此の三直線が同一平面上にある場合とそうでない場合の二つが考えられる。同一点で交わる三直線が同一平面上にある場合の図は各自描いて見るがよい。
一直線と一平面との位置の関係
直線と平面とが若し二点を共有すれば平面の定義によってその直線は全部その平面に含まれ其の直線と平面とは限りなく多くの点を共有することになり唯二つとか唯三つとかの点を共有することはあり得ない。
従って直線と平面の位置の関係には次の通り三つの場合がある。
(1) 直線と平面とが唯一点を共有する場合
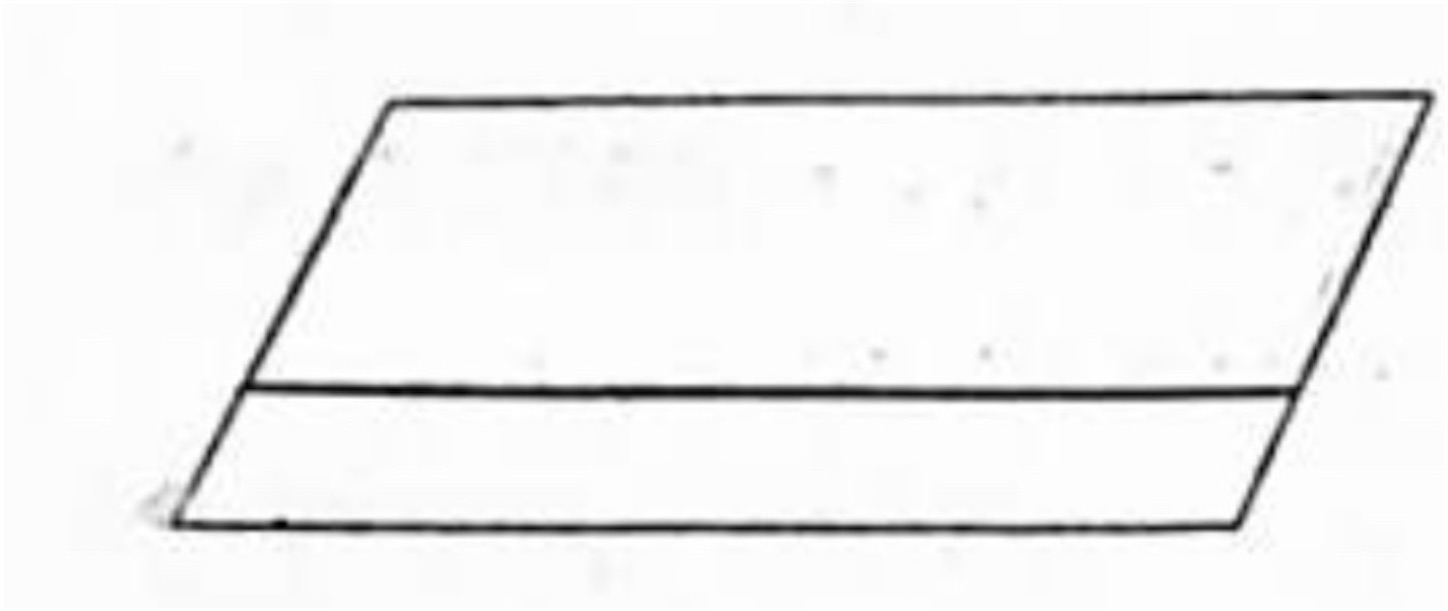
(2) 直線と平面とが無数の点を共有する場合、言い換えると直線が平面の中に含まれる場合
(3) 直線と平面とが一点をも共有しない場合、言い換えると直線と平面とが如何程双方へ延長しても出会わない場合
一直線と一平面とが唯一点で出会うときはその「直線と平面とは相交わる」といい、その出会う点を「直線と平面との交わり」又は「交点」という。
次に天井の線と床の面との関係のように一直線と一平面とが双方に何程延長しても出会わないときには、その「直線と平面とは平行」であるという。
従って直線と平面とが平行なことを証明するには交わりもせずまた含まれもしないことを言えばよい。
二つの平面の関係
空間に於ける二つの平面の位置の関係を考えて見よう。例えば天井の平面と床の平面のように双方に何程延長しても出会わぬ場合と、床の平面と壁の平面のように出会っている場合とがある。二平面が全く重なる場合もあるが重なる前の経過を知らないと区別がつかないから先づ二つの場合に分類される。
偖て床の平面と壁の平面のように二平面が出会うときにはいつも一直線が出来ることに気付くが、平面と曲面又は曲面と曲面とが出会うような場合はそうならないのが普通である。今平面と平面との出会う場合に就ての重要な定理を説明しよう。
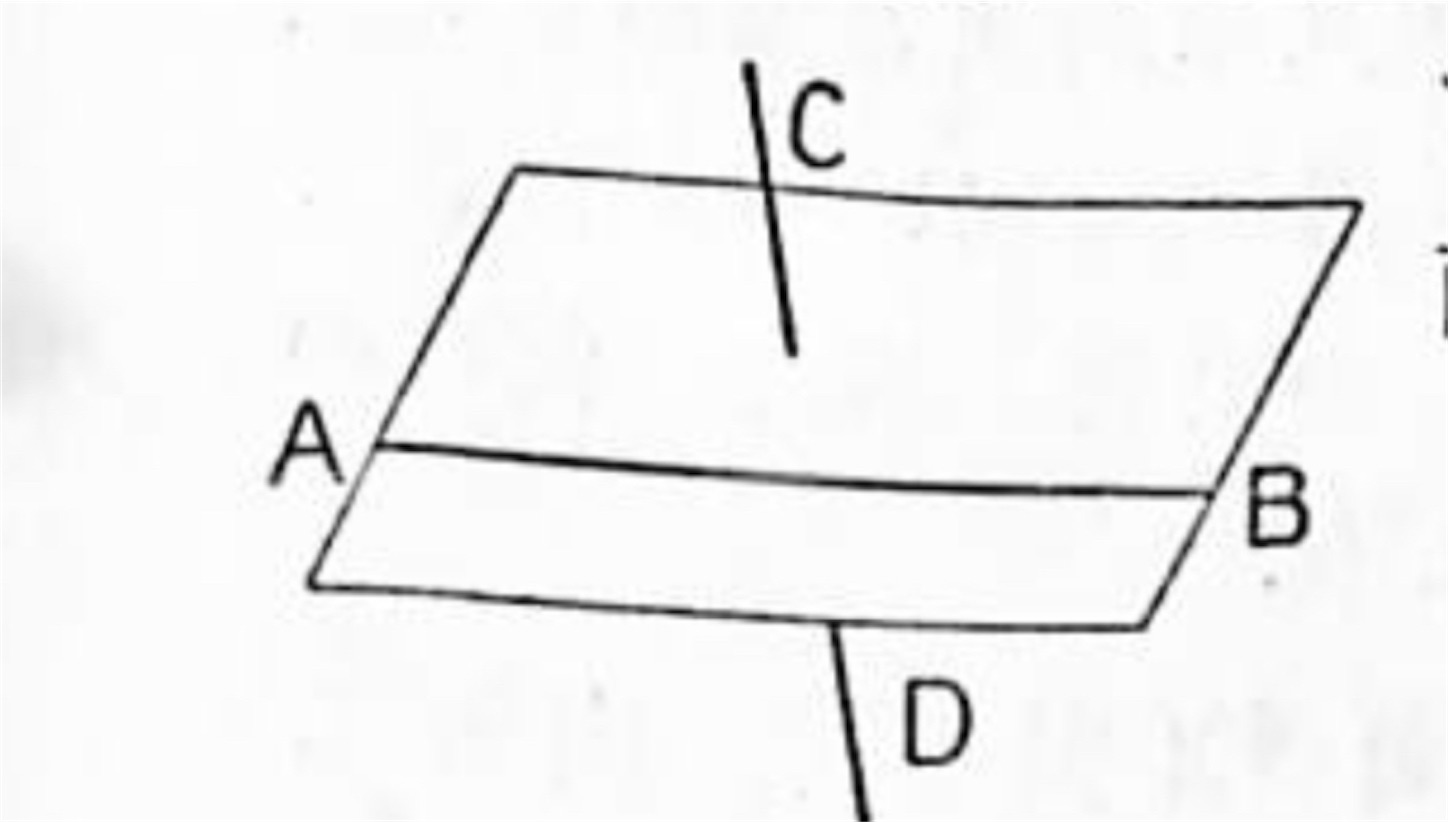
定理 二つの平面 (相異る) が出会うときにはこれ等の平面は一直線を共有しその直線以外の点を共有しない。
題意: P, Q を出会う二つの平面とすると、P と Q とは唯一つの直線のみを共有する。
証明: この定理の証明は仮定をどう定めるかによって非常にむづかしくも考えられるのであるが初歩のことではあるし相異なる二つの平面は「一つの線」で出会うものであると仮定して証明を進めることにしよう。
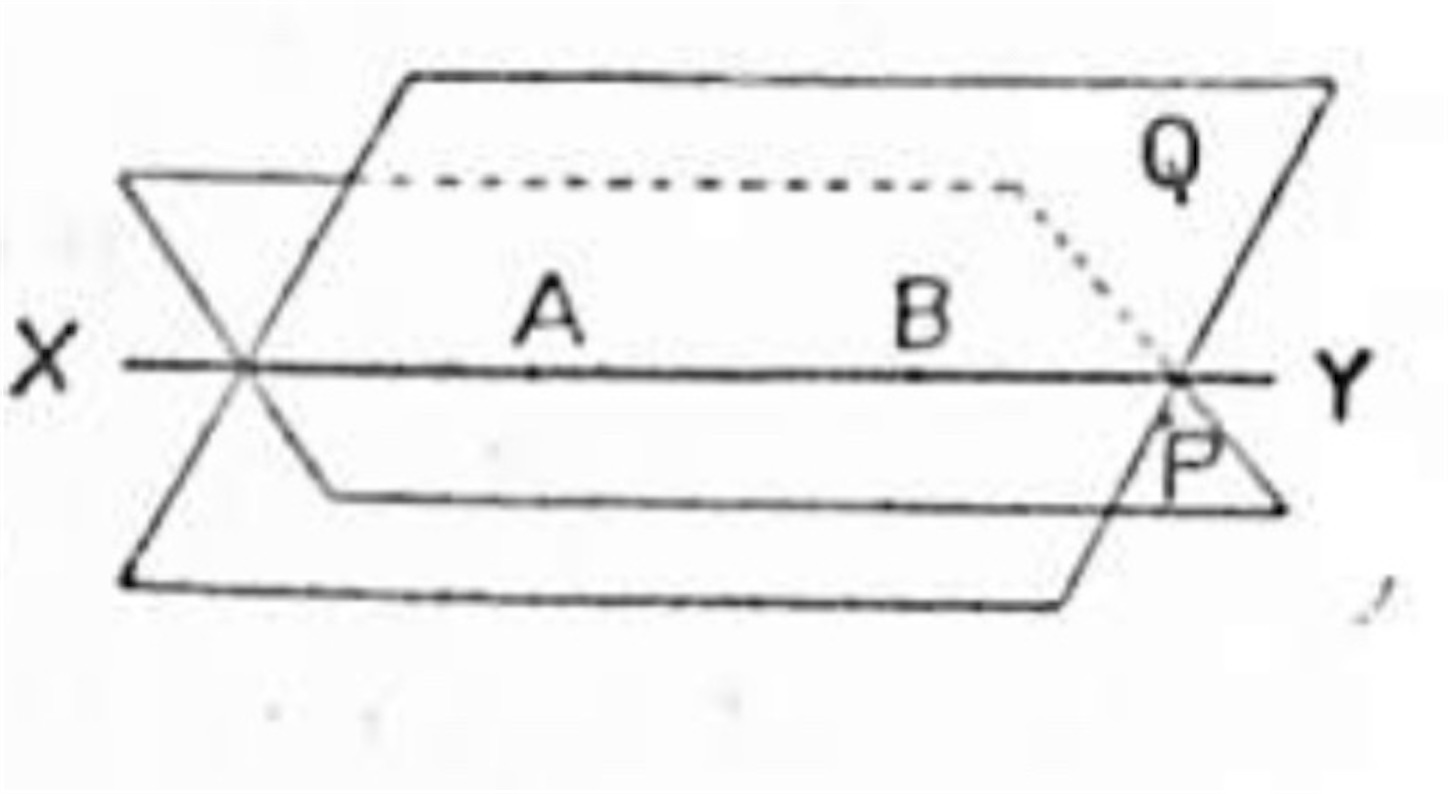
二平面 P, Q が出会う線上に任意に二点 A, B を取ると平面の定義によって直線 AB は平面 P, Q の何れにも含まれる。即ち平面 P, Q は一直線を共有する。
次に平面 P, Q が直線 AB 外に或一点を共有すると仮定すると一直線とその外にある一点とを含む平面が P, Q の二つあることになって平面を決定する条件に反する。故に P, Q は唯一つの直線 AB のみを共有するのである。即ち証明された。▪️
二平面の位置の関係について次の二つの定義を記して置く。
二つの平面が唯一つの直線を共有する時には「二平面は相交わる」といい、その直線を「二平面の交り」又は「交線」という。
二つの平面が双方に何程延長するも出会わないときにはこの「二平面は平行である」という。
依って空間に於ける二平面の位置関係は次のように述べることが出来る。
[I] 平行な場合 [II] 相交わる場合
例題 2. 二つずつ相交わる三つの平面 P, Q, R があって P と Q との交りを a, P とR との交りを b, Q と R との交りを c とするとき、a, b, c の中のいづれか二つが交れば残りの一つも亦その交点を通る。
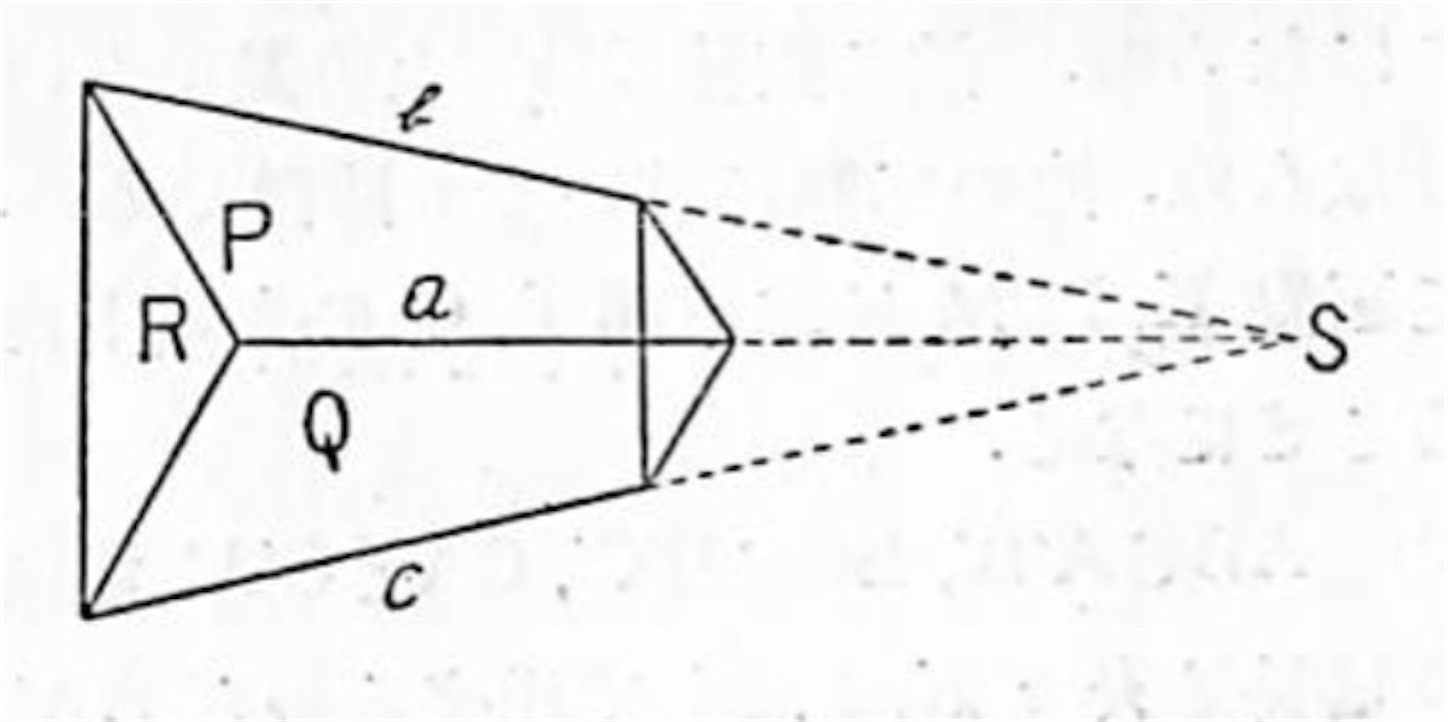
証明: a, b, c の三つの中例えば a と b とが相交わると仮定しその交点を S とすれば、S は a の上にあるから a を含む平面 Q の上にある。同様に S は平面 R の上にもある。
然るに Q と R とは直線 c の他には共有点を持たないから S は c の上になければならぬ。故に c は S を通る。
即ち a, b, c の中何れか二つが交われば残りの一つも亦その交点を通ることが証明された。
例題 3. 同一平面上に無い二つの三角形 ABC, A'B'C' があって AB と A'B', BC と B'C', CA と C'A' 或はその延長とが夫々相交わるときは
(1) その三つの交点 K, L, M は一直線上にある。
(2) 又同名の頂点を通る三直線 AA', BB', CC' の内何れの二つの平行でなければその三直線は同一点に相会する。
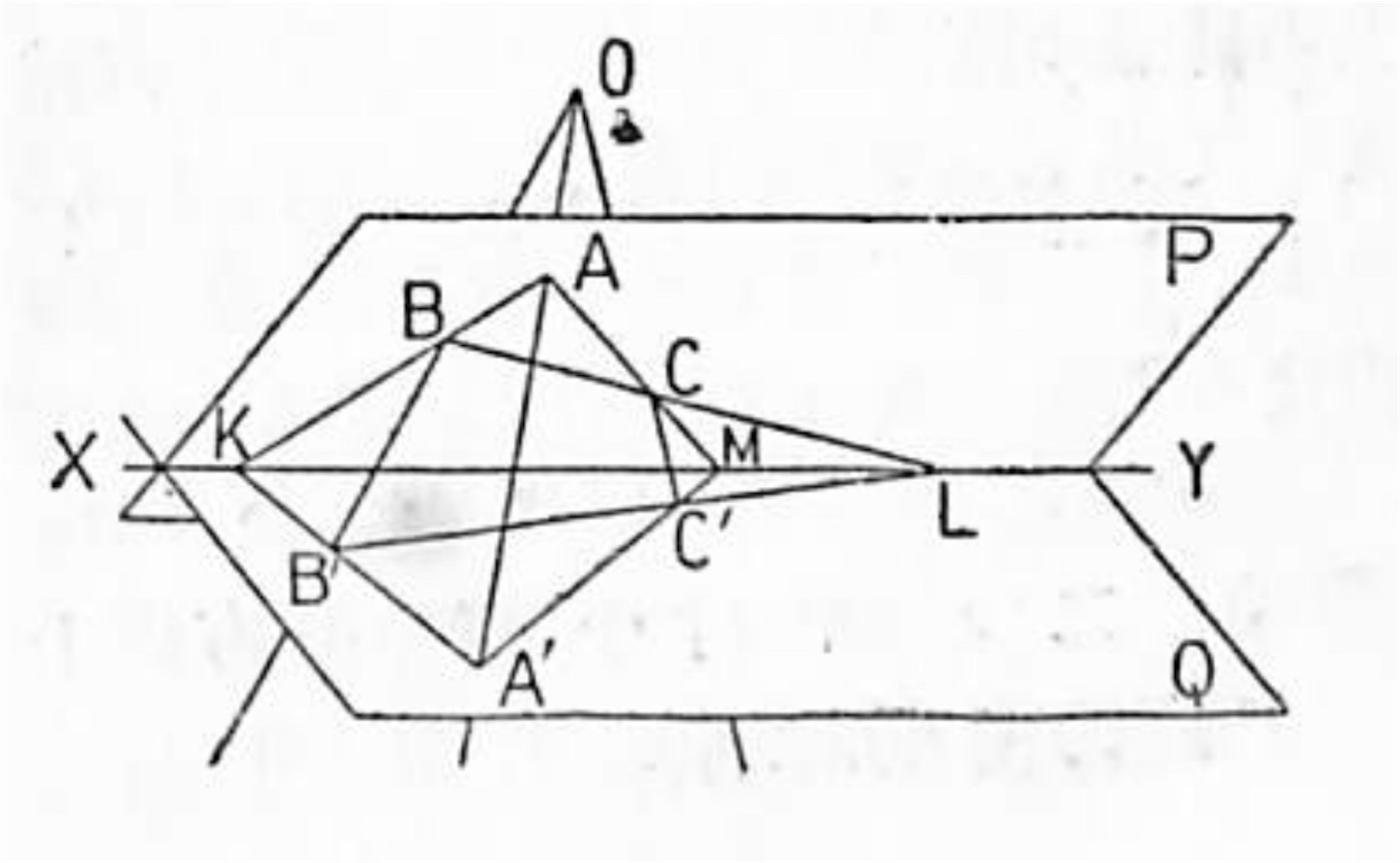
証明:
(1) 三角形 ABC を含む平面を P, △ A'B'C' を含む平面を Q と名付け、且つ此の二平面の交線を XY と名付けると、AB と A'B', BC と B'C', CA と C'A' は夫々相交りその交点が夫々 K, L, M であるから、三点 K, L, M は皆此の直線 XY 上にある。何故かといえば直線 AB は P 平面上にあり、直線 A'B' は Q 平面上にあってその交点が K であるから K は此の両平面 P, Q の各の上になければならぬ。故に交線 XY 上の点でなければならぬ。他の二点に就いても同様である。故に三点 K, L, M は二平面 P, Q の交線上にあることになる。
(2) AB と A'B', BC と B'C', CA と C'A' 或は其の延長は夫々 K, L, M で相交るから AA', BB', CC' の何の二つも同一平面上の直線である。そして仮定によって何れの二つの平行ではない。故に何の二つも相交わる。今 AA' と BB' の決定する平面を R, AA' と CC' の決定する平面を S とすれば R とS とは同一平面ではない。若し R と S とが同一平面だとすれば △ABC と △ A'B'C' は同一平面上の両三角形となって仮定に反するからである。又 AA' は両平面 R, S の何れの上にもあるからその交りである。
今 BB' と CC' の交点を O とすれば O は二平面 R, S の交り上になければならぬ。然して R と S の交りは AA' のみである。故に AA' は O を通り三直線 AA', BB', CC' は同一点 O に会する。
問題 2. 二つの平面 P, Q が平行であれば P 上の任意の直線と Q 上の任意の直線とは相交わらないことを証明せよ。
P 上の任意の直線を a, Q 上の任意の直線を b として若し a とb が相交わる とすれば、 a, b は夫々 P, Q 上の直線であるから P, Q 二平面が相交ることになって仮定に反するからである。
問題 3. 二つの平行平面の一方の上にある任意の直線は他の平面に平行である。その理由を説明せよ。
平行二平面を P, Q とし P の上にある任意の一直線を a とする。P と Q とは平行であるから共有点を持たない。故に a と Q とも亦共有点を持たないことを考えるとよい。
問題 4. 線分 AB の両端を通る平行線 AA', BB' と AB の中点 M を通る任意の平面 P との交点を夫々 A', B' とすれば AA' = BB' となることを証明せよ。
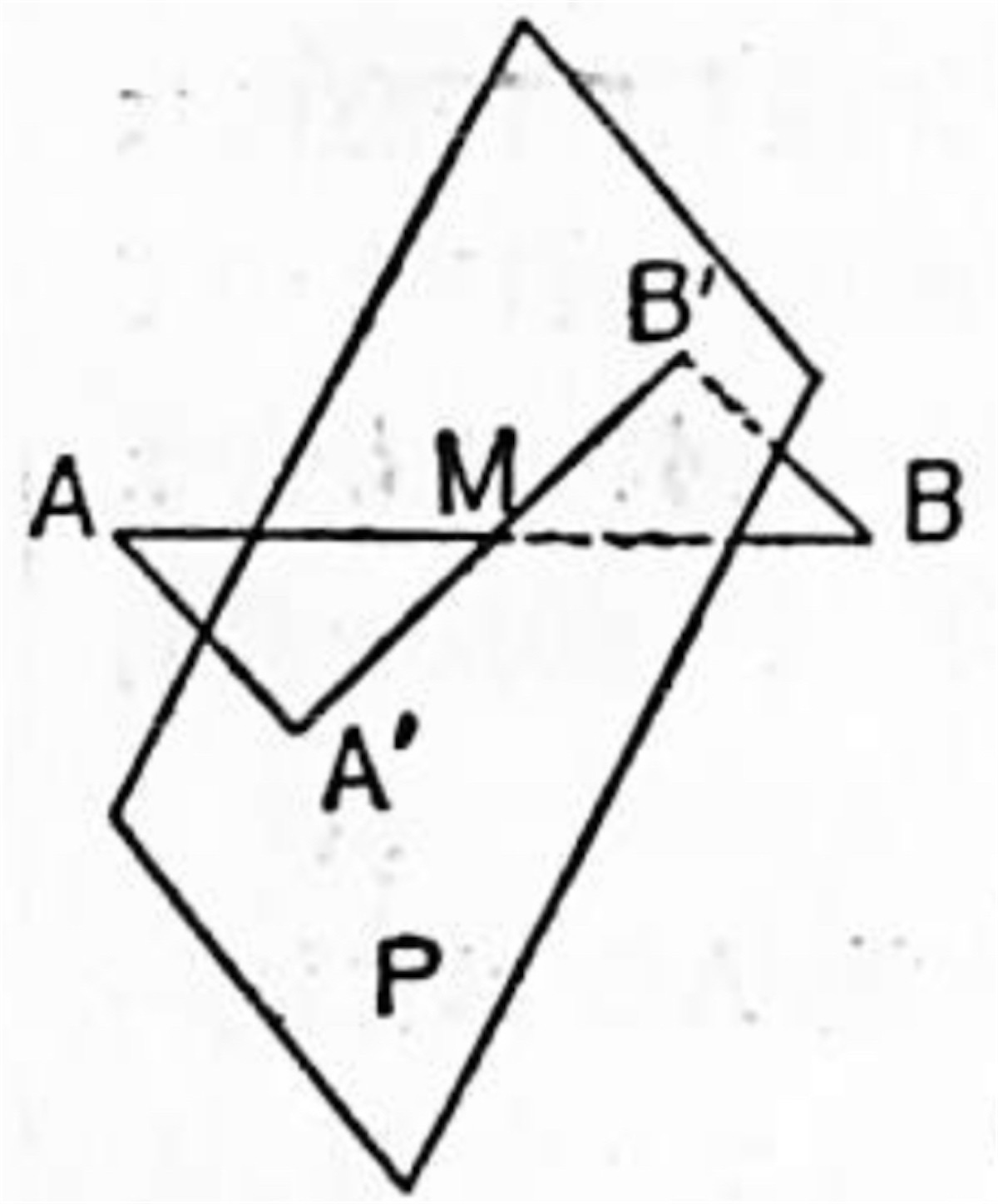
題意によって AA' と BB' とは平行であるから一平面を決定する。今この平面を Q とすれば AA', BB' は Q 上の直線であるから A', B' の二点は勿論 Q 上にある。又 M も Q 上にある。又 A', M, B' の三点は P 上の点でもある。従って A', M, B' の三点は P, Q の交線上にあって一直線をなすことから △ MAA' と △ MBB' に就て考えるとよい。
問題 5. 同一平面上にない二つの直線 AB とCD 及びその何れの上にもない一点 M とを与えて M を通りこの二直線と交わる直線を作れ。
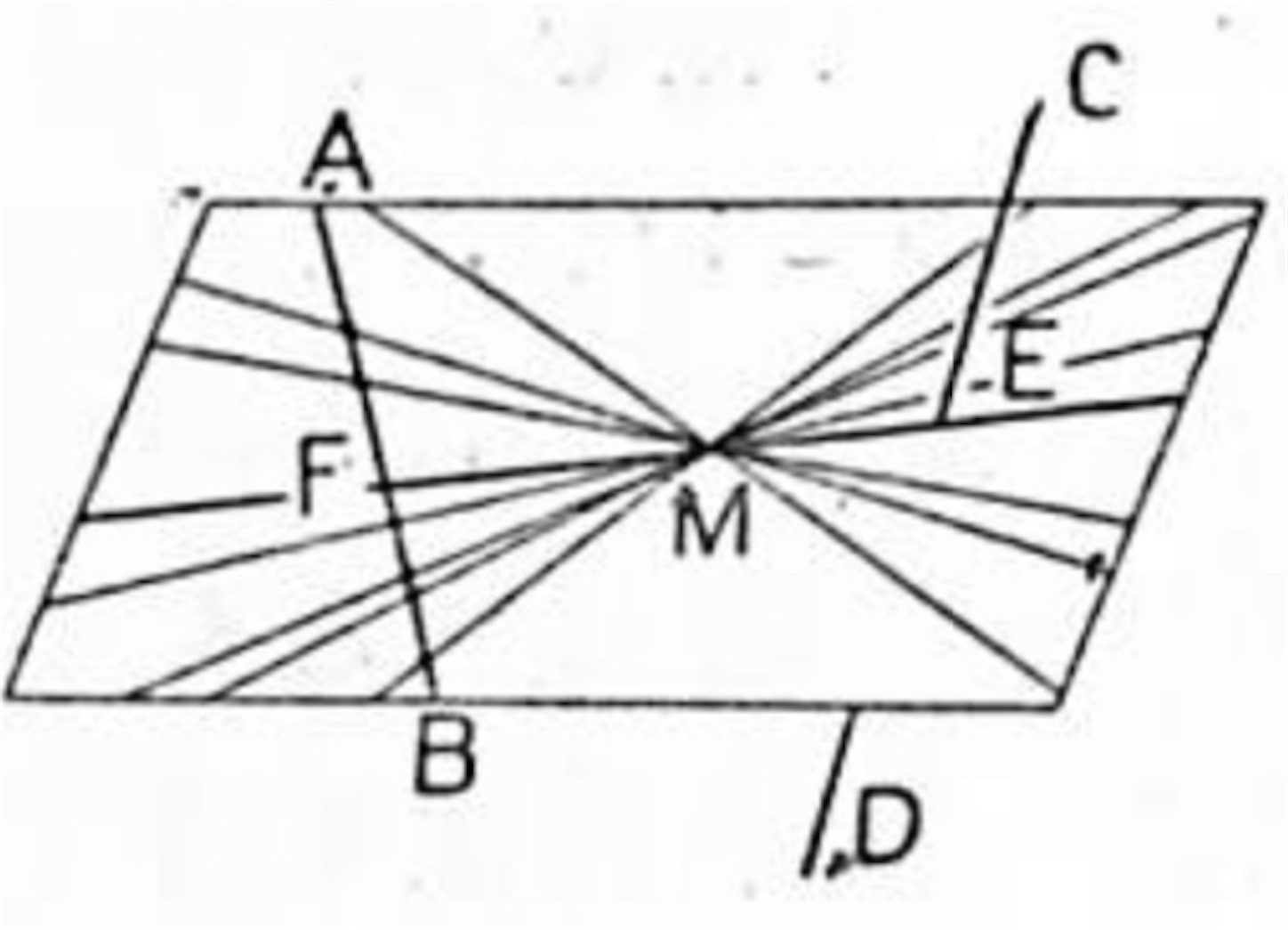
M を通り AB と交わる直線は無数にある。従ってその中の一つに CD にも交わるものがあることになる。そして M を通り AB と交わる無数の直線は何も M と AB との決定する平面上にあることに気付くと M と AB との決定する平面 P を作り之と CD との交点 E を求めて平面 P 上で二点 M, E を通る直線を引けばよい。今 ME と AB との交点を F とすれば EF は求める直線であるが平面 P が直線 CD に平行となる場合、又 ME が AB に平行となる場合には解はない。