陥没地帯 (33) - ノリの悪い日記

中学 3 年の理科で星 (恒星)や太陽を地球から見たときの動き方を習うが、大人になってさえ基本的な動き方を理解していない人が多いのはなぜだろうと考えた。自分が思うに、太陽を除く恒星の見かけの動きと太陽の見かけの動きの違いが不十分にしか理解されていないからなんではと思う。

まず天球図とかにいきなり入る前に上のような図を漠然としかみていないところに問題がある。そもそも、公転 (地球の公転軌道は半長軸約 1 億 5 千万 km = 1 天文単位のほぼ円軌道である。そうするとケプラーの面積速度一定の第二法則——角運動量保存則に他ならない——から地球の太陽に対する速さはほぼ一定である) が 1 年かけて地球が北極星から見て反時計まわりに 1 回自転する (回転方向は 1 日の地球の自転と同じである) のと同じ効果をもつという認識がまず必要で、その認識の上で地球の公転は太陽と他の恒星の見かけの動きにまったく異なる結果をもたらすことが上図からわかる。

夏至と冬至で考えれば、公転による 180 度回転の影響を差し引けば、太陽が南中する時刻は冬も夏も変わらないことがわかる。つまり、太陽は公転の回転中心なので、公転によって地球から太陽が回転して見えることはなく、太陽が回転したとすれば、それはあくまで地球の自転だけの影響である。けれども地軸 (地球の自転軸) が公転面の回転軸から 23.4 度傾いているために地球の自転軸は公転によりコマの首振りのように 1 年に 1 回転する。そうすると太陽の南中高度は冬と夏では違う (もちろん地球の北半球では夏は高く、冬は低い。南半球の同じ時期では逆の関係である)。

一方、他の恒星は公転の回転中心にはいないので地球の公転により、自転で見えるのと同じ方向に 1 年に 1 回の周期で、回転して見える。このとき、地球の自転軸の首振りも同じだけ回転するので、公転軌道のどの位置でも観測者から見た同じ星の南中高度は常に一定で変動することはない。たとえば、冬は深夜にふたご座が南中して見えるが、夏は真昼に南中するので見えない。しかし、もし見えたとしたら南中高度は変わらない。

以上から公転の影響により太陽は南中高度が変わるが、他の恒星では 1 日約 1 度天球を先に回転させるという効果の違いがあることが理解できる。それが理解できれば観測者を中心に半径の巨大な球を書いて、中心の北方向から緯度 (この辺だと北緯 35 度くらい) の角度の線を引けばそれが地軸の方向である。

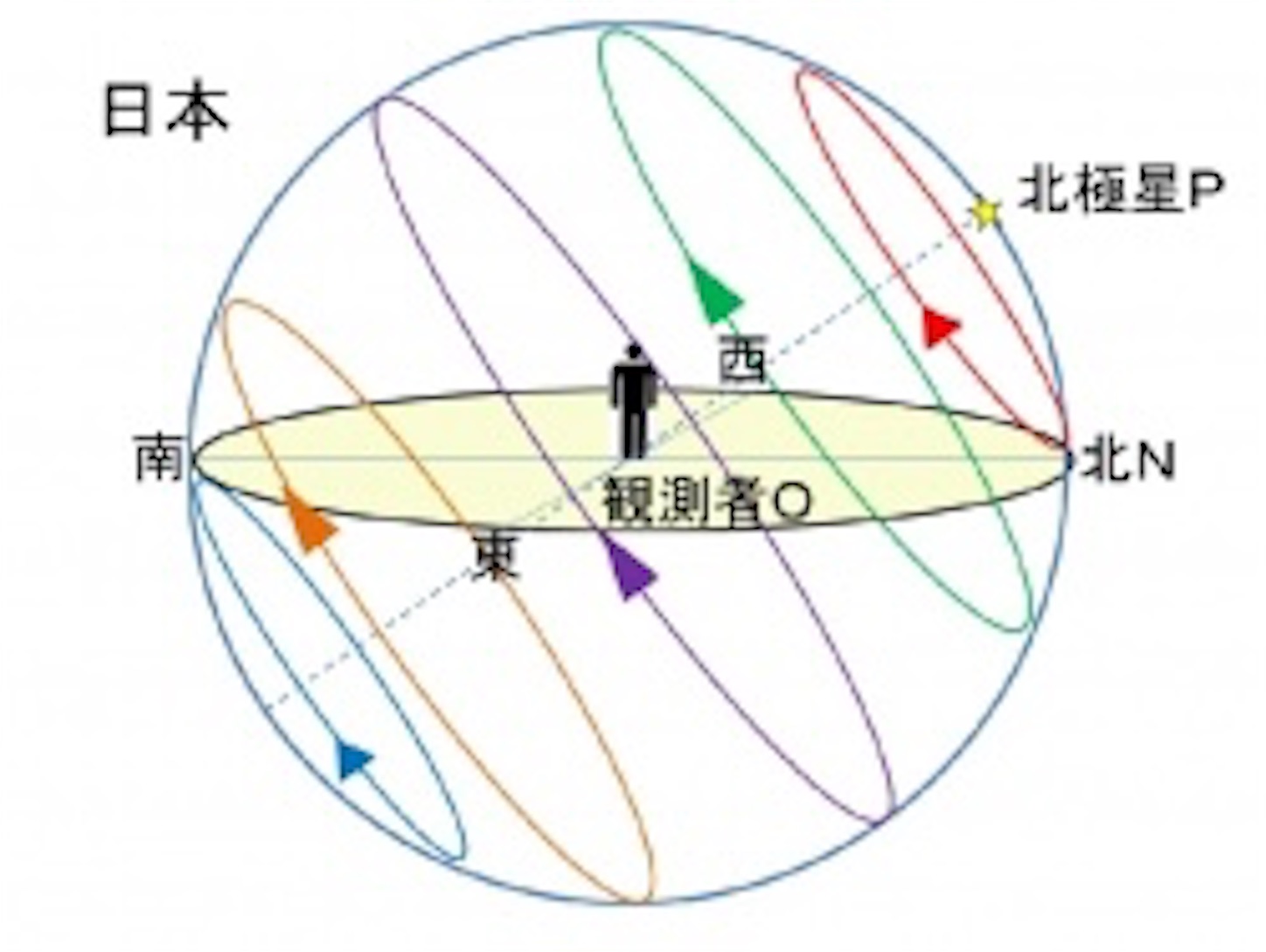
そして球全体を観測者から北を見て反時計まわりに回転すれば良い (もちろん南の方を見れば時計まわりである)。太陽以外の恒星は球に張り付いていて球全体が北を見て反時計まわりに 1 日に約 361 度回転する。1 度はもちろん公転の影響である。太陽は他の恒星とは違って地球の自転にあわせて1 日に 360 度回転する。しかし、南中高度は変化する。春分と秋分 (3 月 / 9 月) は天の赤道を通る。そして太陽は、夏至 (6 月) のときは春分・秋分よりも地軸の傾きである 23.4 度高い南中高度で回転する。もちろん、回転軸は変わらないので、日の出、日の入りの方角も平行に北方向へ移動する。冬至 (12 月) のときは春分・秋分よりも地軸の傾きである 23.4 度低い南中高度で回転する。もちろん、回転軸は変わらないので、日の出、日の入りの方角も平行に南方向へ移動する。

以上これだけ、最低きちんと理解できていれば中学段階の基本としてはよい気がする。

※ 日影曲線というのがあって、これは地面に棒を垂直に立てて、地面に落ちた棒の太陽の影の先端軌跡が日の出から日の入りでどんな線になるかという問題である。これは中学理科の範囲では白眉の面白い思考実験である。

太陽光は他の恒星からの光と同じように平行光線とみなす重要な仮定を暗黙でしている (大気の高度で変わる密度の違いによる光線の屈折さえ無視する) ので、地面に垂直に立てた棒の垂直 (鉛直) 度に問題がなければ、棒の先端を天球の中心点にとって構わない。太陽の (夜も含めた) 移動軌跡はもちろん円だから、その円と棒の先端が囲む立体は一般に円錐である。その反対に棒の先端を通過した太陽の光によってできる円錐と、観測中心の棒の長さだけ下にある水平な地面 (切断面) が交わった輪郭線が棒の先端の影の軌跡となる。つまり日影曲線とは円錐曲線に他ならない。

特別な場合として春分、秋分で太陽が天の赤道を通る場合は、円錐の高さがなくなってしまうが、この場合は、世界中 (北極点、南極点を除く) で日影曲線は直線となる。春分と秋分で日影曲線が直線となることを以下に簡単に証明しておく。

(以下証明)
棒の頂点 (天球の原点) は太陽の軌道を含む平面上にある。したがって棒の頂点を通過する光線はすべて太陽の軌道を含む平面上にある。平面と平面の交わりは一般に直線である。以上より日影曲線は直線である。
(証明終わり)

円錐曲線には円、楕円、放物線、双曲線、直線が可能だが、いずれも地球上のある場所、ある時点で日影曲線として見られるはずであり、考えると結構面白い。

(円錐曲線が楕円、放物線、双曲線になることの証明は他のサイトにもあるので省略する。特に円錐の内接球で切断面にも接するものを考え、球の外部の一点を通る任意の球の接線の外部点から接点までの長さはみな等しいという、三角形の合同から容易に証明できる事実を巧みに利用した幾何学的証明は目から鱗が落ちるような、きわめて美しい味わい深さをもっている。放物線の証明はこの三つの中では一番難しいが、副産物としてパラボラアンテナの原理が理解できる。)

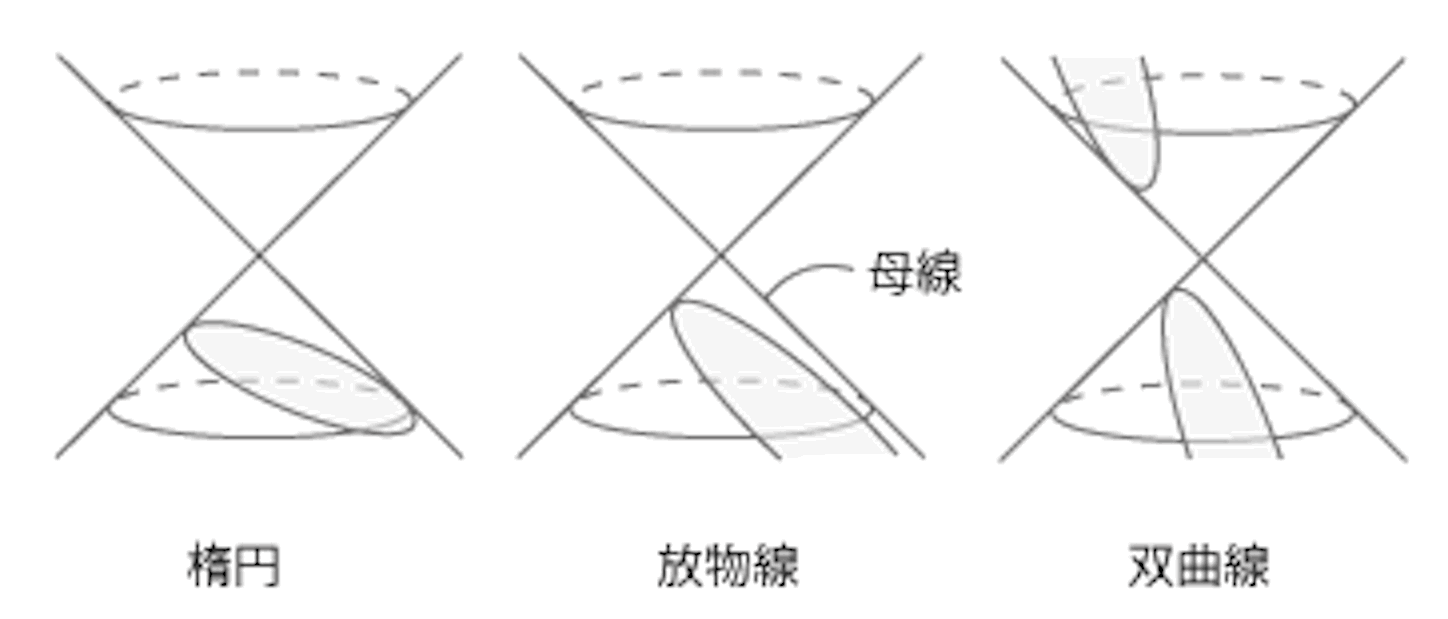
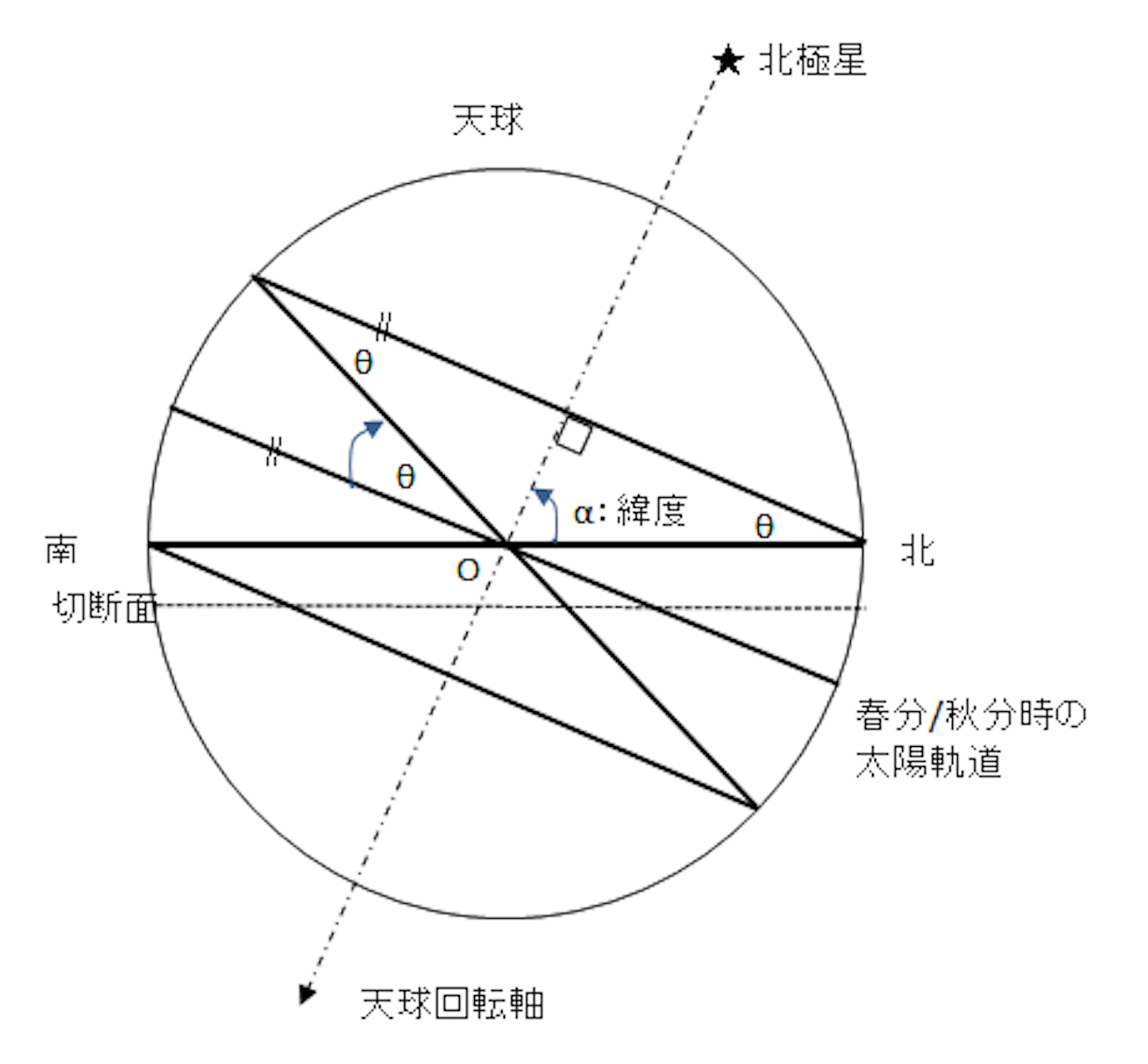
条件的にいちばん難しいのが放物線だと思う。双曲線は頂点を共有し向かいあった二つの円錐の両方に同一平面 (ただし円錐の頂点を含まない平面に限る) による切り口ができるときに現れる線なので、日没がある地域においてもっとも普通に見る日影曲線といってもよいと思う。別の言い方をすれば、円、楕円、放物線が日影曲線として見られるのは、白夜のある南北両半球の高緯度地域に限られるということである (円が見られるのは南北の極点に限られる)。放物線ができるには地面 (切断面) と円錐の母線が平行という条件を満たさなければいけないので、日影曲線が放物線になるには一日 24 時間、太陽が没しない白夜でかつ真夜中に太陽が観測水平面と北で接するという条件を考察する必要がある。作図すると (下図参照) 北半球では緯度 $\alpha$ と春分または秋分のときからの太陽の高度の時計まわりの上昇角 $\theta$ が

$\alpha + \theta = \pi /2$

を満たすとよいことが二等辺三角形の性質からわかる。もちろん $\theta$ は公転面法線からの地軸の傾き 23.4 度以下であることを満たさないといけないので、北緯 66.6 度よりも高緯度地域 (つまり、北極圏と南極圏) の 3 月から 9 月の間に一度 (夏至に条件を満たすとき) または二度 (夏至以外で条件を満たすとき) しか起きず、具体的にいつ起きるかは緯度に依存するということになる。

【問題】

素数 $p, q$ を用いて

$p^q + q^p$

と表される素数をすべて求めよ。

【解】
$p^q + q^p \gt 7$ であるから、 $p^q + q^p$ は奇数の素数である。このことから、 $p \neq q$ である。また、 $p^q, q^p$ のどちらか一方は偶数で、もう一方は奇数であることから、 $p, q$ のどちらか一方は $2$ である。どちらを $2$ としても、式の対称性から結果は変わらないので、 $p = 2, q \gt 2$ として議論する。