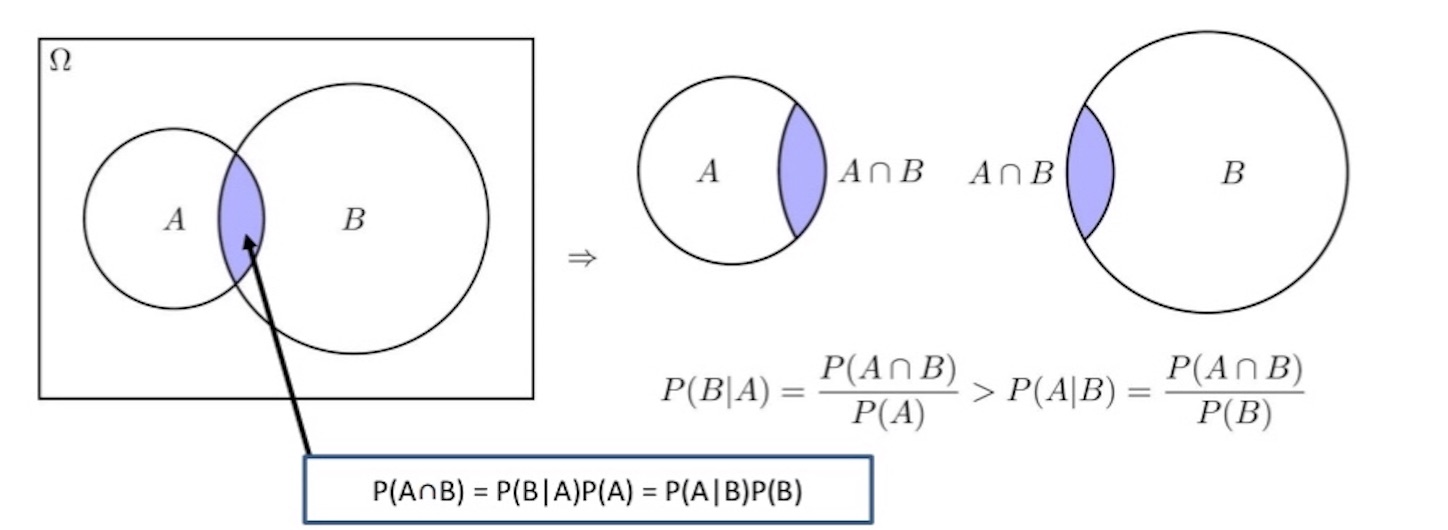
いままでの記事で「等確率バイアス」とか「対称バイアス」といっていたものを補足しておくだけの記事である。知っている人にはきわめて初歩的なものでつまらないと思う。
【問】
乳がん検査に参加した 40 代の女性に乳がんがある確率は 1% です。女性がもし乳がんならば,検査で陽性となる確率は 80% です。ただし女性に乳がんがなくても、検査で陽性となる確率が 9.6% あります。
検査に参加した 40 代のある女性が陽性でした。この陽性の女性が実際に乳がんである確率はどのくらいでしょうか?
上の問題を、計算ではなく直感で (専門家ではない人に) 回答させるとかなり多くの人が 80% と回答するらしい——もちろん誤答である。「らしい」というのは不特定多数相手に自分で実験したわけではないからである。ただ、自分が初めてベイズの定理に触れた学生時代の記憶でも、なんか当たり前の定理で、いったいなにが嬉しいんだろうとちょいと不思議だったし、ごりごりやった計算結果が直感とかなりずれている気がしたことも確かに覚えていて、80% という回答はわかる気もするのである。
で、これがなぜ、「対称バイアス」であるかというと、単純に
とみなしているからである。ちょうど命題論理で一方が成り立てば ()、逆命題 (
) も自動的に成り立つと仮定するバイアスの類推で、これも「対称バイアス」と呼んでいる。
ところで、
だから、
ということは、
と、基準となる確率 (基準率 basic rate) を等しいとみなしているので「等確率バイアス」と呼んでもよいではないかということである。
※ なので、この関係については対称性が成立している。//
以上から、問題には直接示されていない がどの程度の大きさか見積もること——
と何倍ぐらい違うかを見積もること——が正しい直感にたどり着くためには不可欠である。
集合のベン図を頭の中で書いてみると (この記事の一番下の図参照)、
が恒等的に成り立つので、
→ たいだい 9.5%
となる。したがって、
となり、 は、
とくらべて、10.3 倍大きいということになる。
したがって、正解は
で約 7.8% となり、誤答である 80% よりは随分小さい値となる。
※ 以下は用語の問題にすぎないが、問題文において検査で乳がんがあるものが陽性 (positive) となる確率 80% を “感度 sensitivity” が 80% であるという。このとき、見逃し率 (間違った陰性) は 20% あるが、これを “偽陰性率 false negative: fn ” が 20% という。また、乳がんではないのに間違って陽性と判定する率 9.6% を “偽陽性率 false positive: fp” が 9.6% であるという。また “特異度 specificity” というのは乳がんでない場合を正しく陰性 (negative) として判定する確率のことを指し、この場合、100 - 9.6 = 90.4% である。最後に、 は “陽性的中率 positive predictive value: ppv” と呼ばれる。一般に陽性的中率は、感度、特異度だけでなく検査を適用する集団の “有病率 prevalence” の影響も受ける。つまり、ベイズの定理から、
が成立し、これを言いかえれば、
陽性的中率 陽性率 = 感度
有病率
ということである。ここで、「陽性率」は先ほどの考察から、
陽性率
= 感度 有病率 + 偽陽性率
(1 - 有病率)
= 感度 有病率 + (1 - 特異度)
(1 - 有病率)
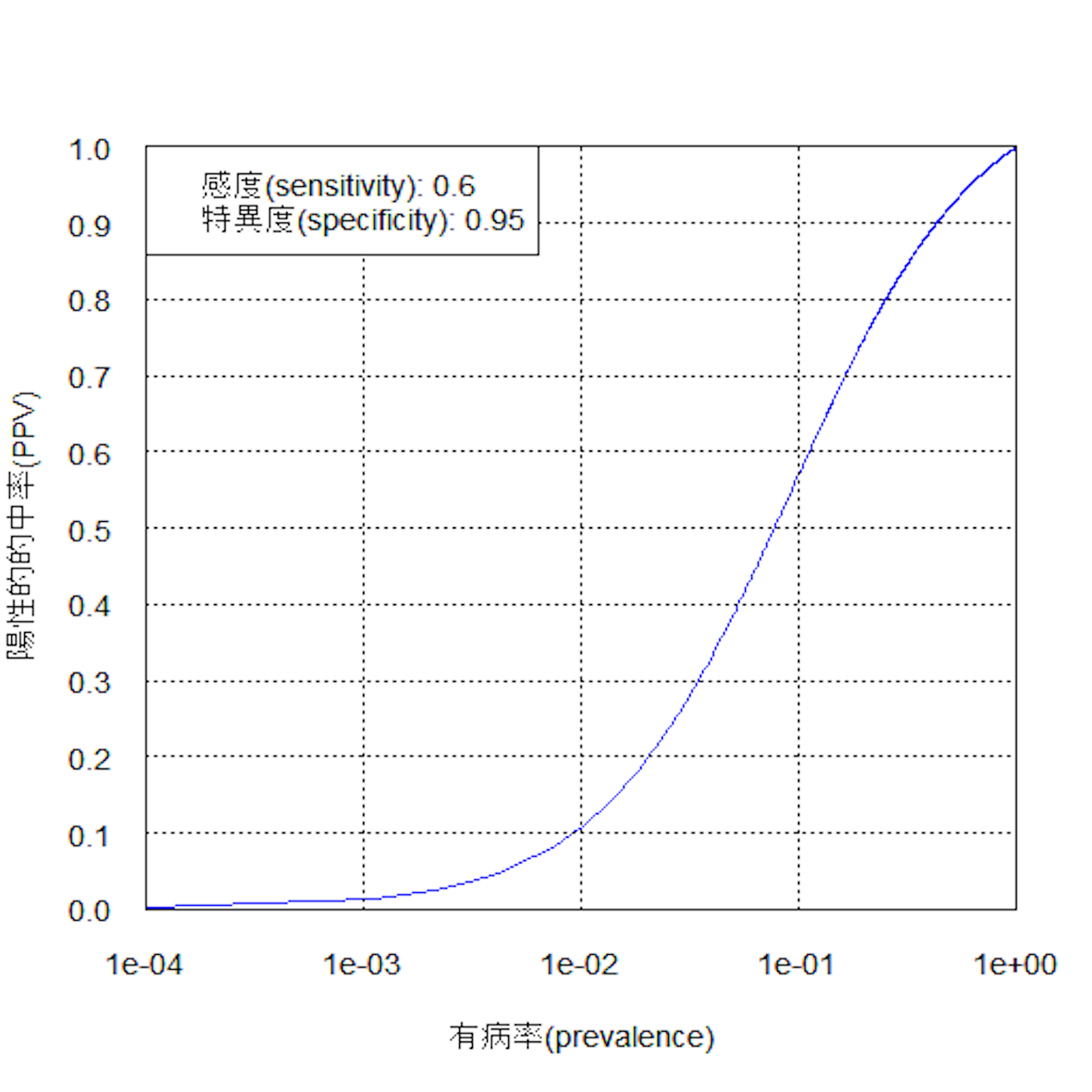
となるので、結局、陽性的中率は感度、特異度、有病率の函数である。例として、感度が 60%、特異度が 95% の検査を適用したときに、適用集団の有病率によって陽性的中率がどう変わるかのグラフをあげておく。
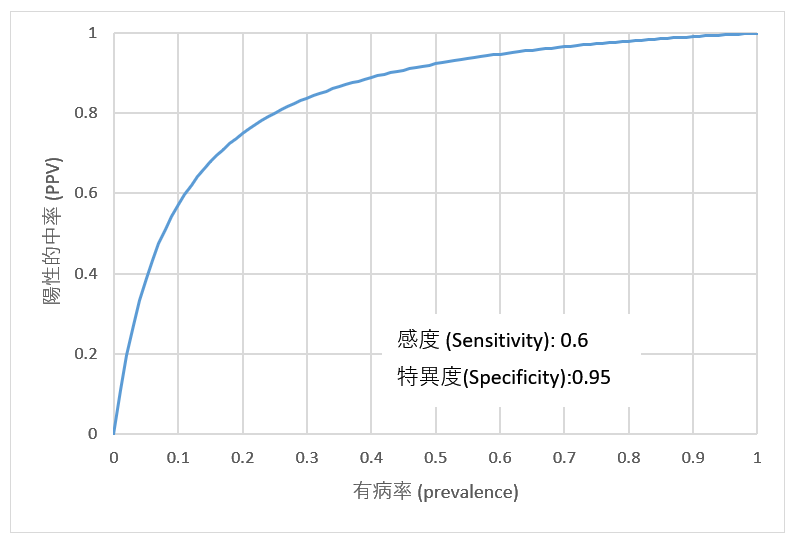
なお、横軸を対数目盛にすると、よく見かけるグラフになる。
で定義される「オッズ」と呼ばれる確率と同相なパラメータへ変換すると、前述の関係から
という、ベイズ統計的にはよりすっきりした表示となることがすぐに示せる。ここで、
は、“(陽性)尤度比 likelihood ratio: LR” と呼ばれる。