前回の記事「古論理」を書いてから、この辺りのことを調べていたら、すごく奥が深いし拡がりもあることがわかった。だけど、いくらノリが悪いといっても、西田幾多郎とか、中村雄二郎の「述語的世界」とかの哲学をブログに書いてもなあ〜と思って、自粛していた。
それから認知科学の「対称性バイアス」とかも調べた。これはなかなか面白くて、「対称性バイアス」とは、論理でいえば「p ならば q である」ときに「q ならば p である」も仮定してしまうバイアスのことだが、古論理も一般化してしまえばこの「対称性バイアス」がもとになっていると考えられる (論理的に正しい三段論法の前提条件のひとつを逆にしてしまえば古論理になる)。へー!と感心したのは、対称性バイアスは人間にしか見られないそうで、他の哺乳類、たとえばチンパンジーはアイちゃんみたいに賢くても難しいそうである。つまり、絵 (p カード) をみせて特定の q 食物を選択することが訓練できたとしても、q 食物を見せて p カードを選択することは非常に困難であるそうだ (論理的にはチンパンジーの方が正しいのだが)。
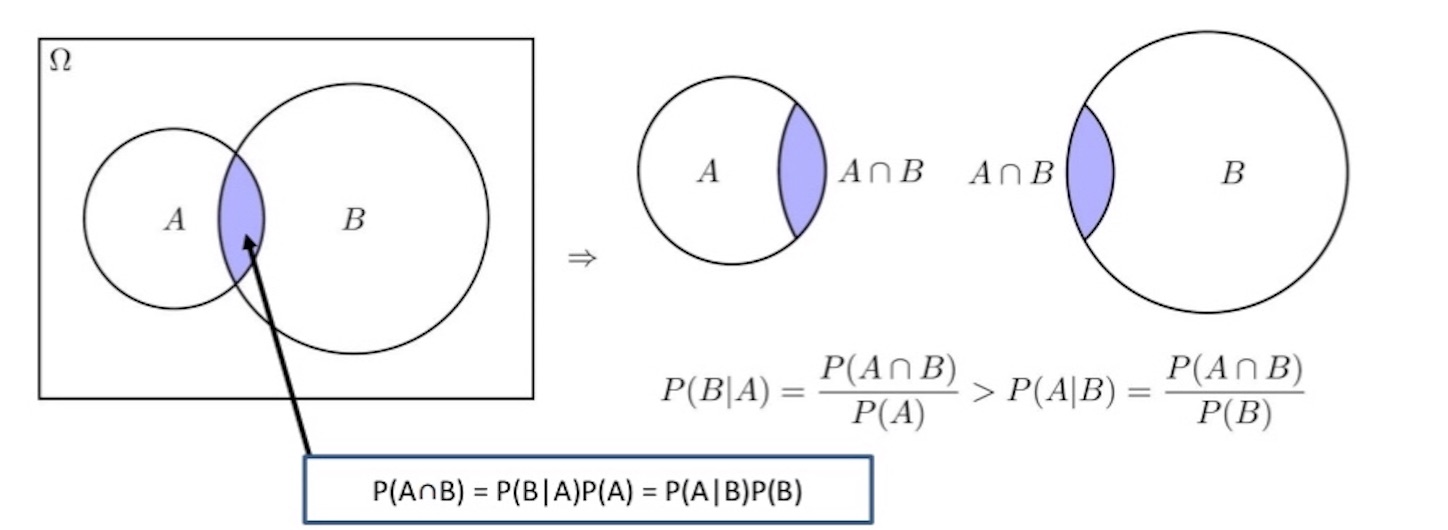
人間の場合、記号のシニフィアンとシニフィエは可逆に結合していないと、まともに会話もできないので対称性バイアスは必要である。そもそも、いくら論理的に正しくなくても、ヒューリスティックスにおいては対称性を仮定してみないと実用的にうまくいかないことは多々ある。それとは逆に対称性を無意識に仮定するために、ほんとうにバイアスとなってしまう場合も確かにある。ベイズの定理なんかがそうで、最初に例題をやったときには、ちょっと直感に反しているような気がする。たとえば、ある A 病気のとき、B 検査で陽性になる確率は 80 % だが、B 検査が陽性のとき 病気 A がある確率は 2 % とかの場合である。これは A が起きる確率と B が起きる確率を無意識に等しいと対称的に考えてしまうバイアスのためである。下の図を見れば一目瞭然であろう。