例年より小問がひとつ減った.

【解】
(ア) 同じような問題を中 1 の定期テスト対策でやったばかりである. 直線と平面の垂直を理解していることと, ピタゴラス (三平方) の定理の基本問題である. 暗算できるだろう. 答えは 2 番.
(イ) 展開図を描き直すときにわからなくなるむきは「有向角」を使うと考えやすい.
(余弦定理を使ってもよいし, これくらいだったら平面座標において 点間の距離を計算したってよいわけだが……)
の長さを求めるために補助線を引く(
,
).
だから,
から,
したがって,
//
下の問題の正解率がどの程度か知らないが, 方程式で解けばよいのだから, 算数は不要だという俗説は嘘だと思う. 算数が理解できないと (この場合は四則の意味をどの程度理解しているかということであり, 私見では「みはじ」のようなものは理解しているうちに入らない), 方程式の立式すら満足にできなくなるという現実をよく見るべきだろう.

【解】
食塩水は最初も最後も g のままである.
食塩は最初に g, 次に
g, 最後に
g で, これが
g に相当するから,
//
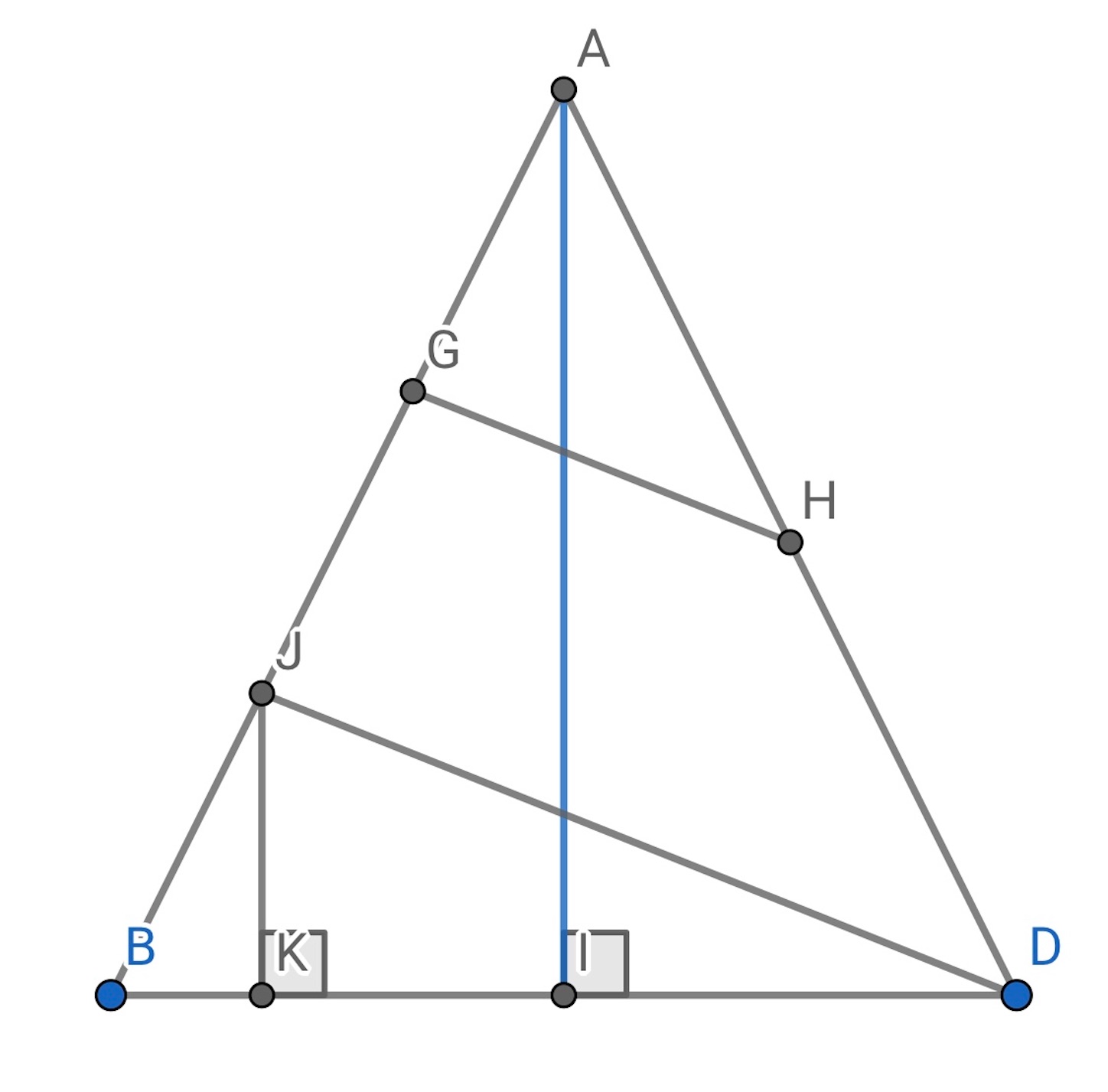
特殊角を使う問題。
【解】
は正三角形. したがって,
は二等辺三角形. 線分
の長さを求めることは平行線
と
の距離を求めることに他ならない.
したがって,
//
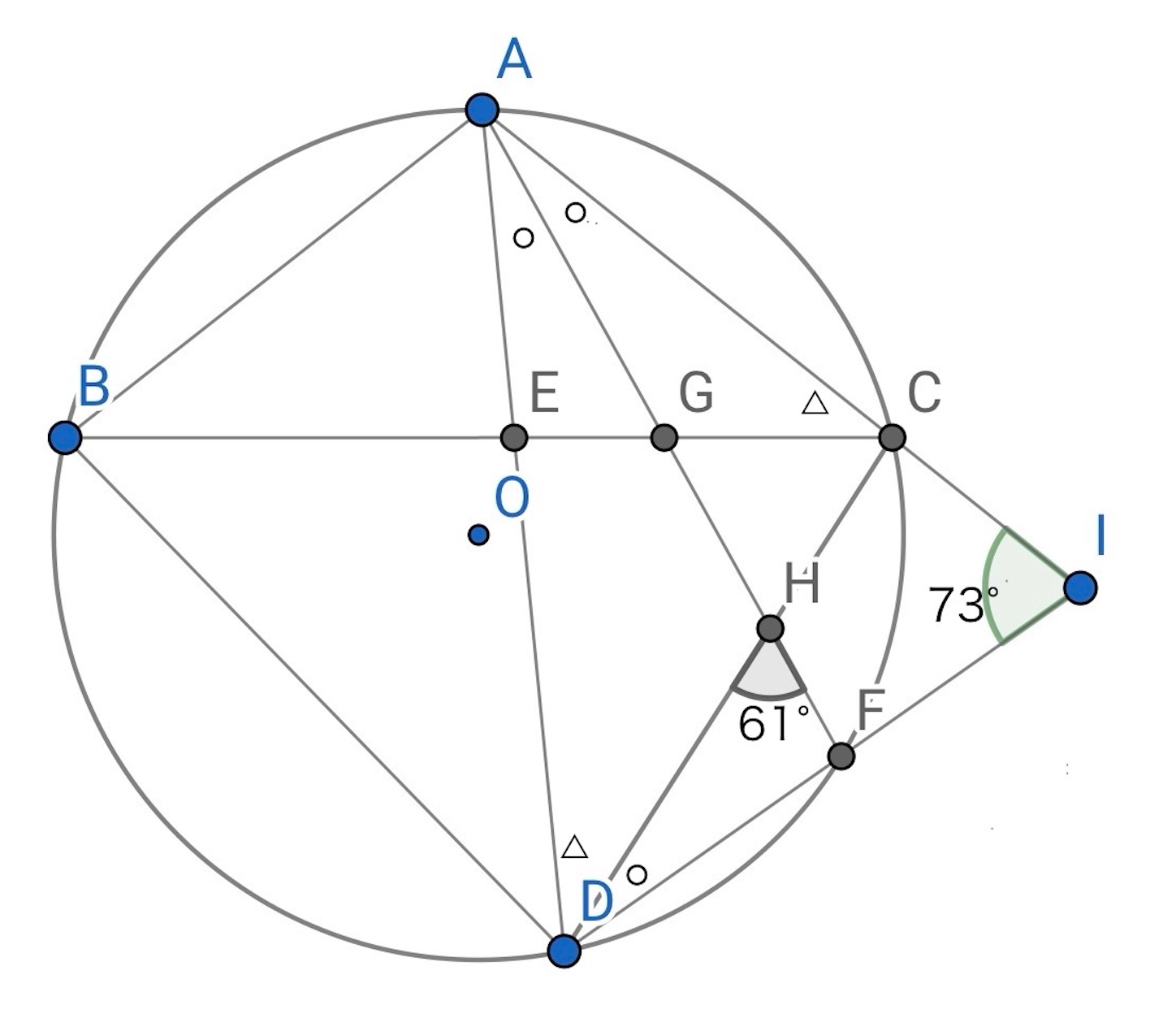
図形の他の問題は,

【解】 (ii) だけ解答する. 下図で,
だから,
だから,
である.
//
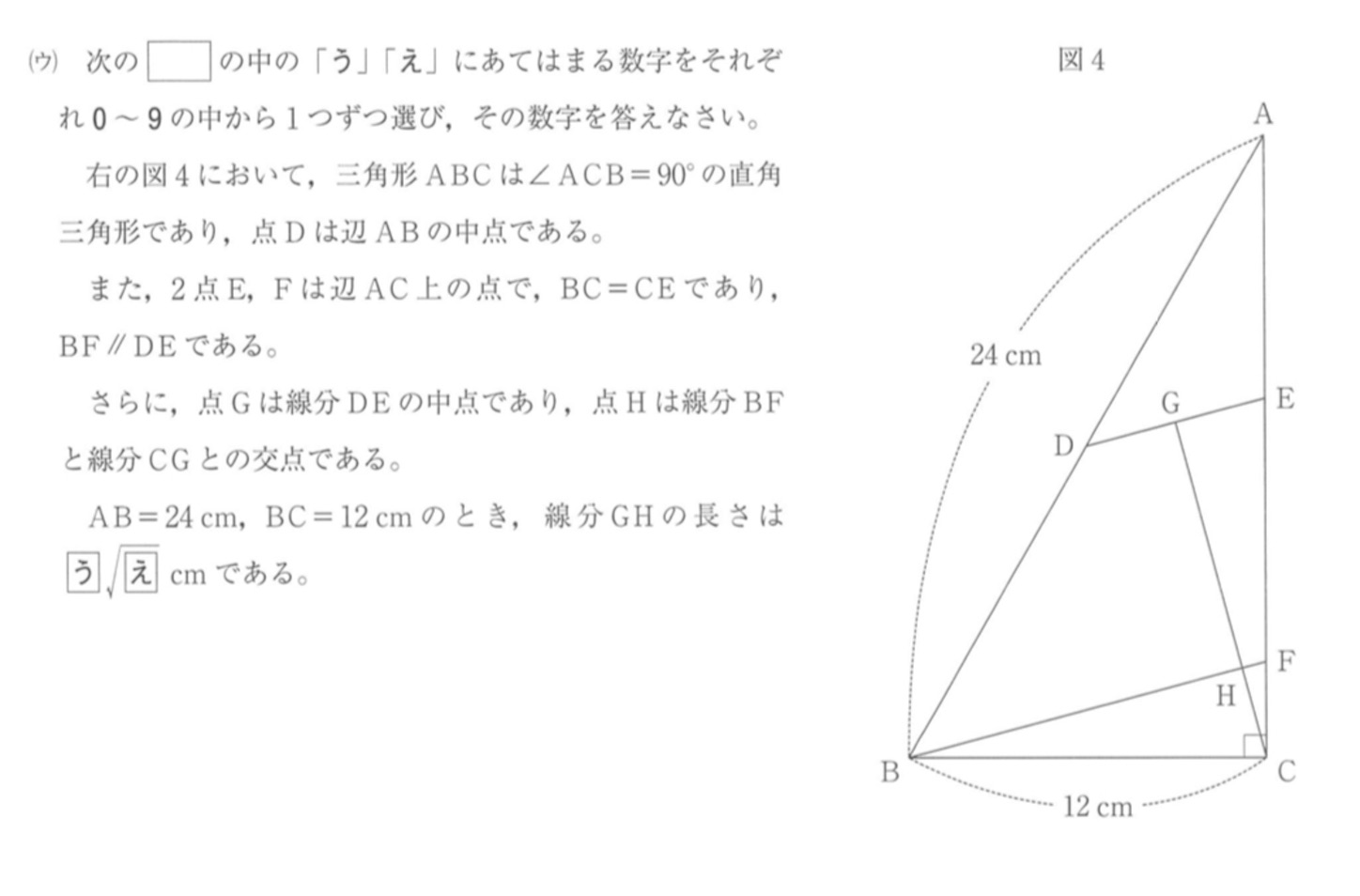
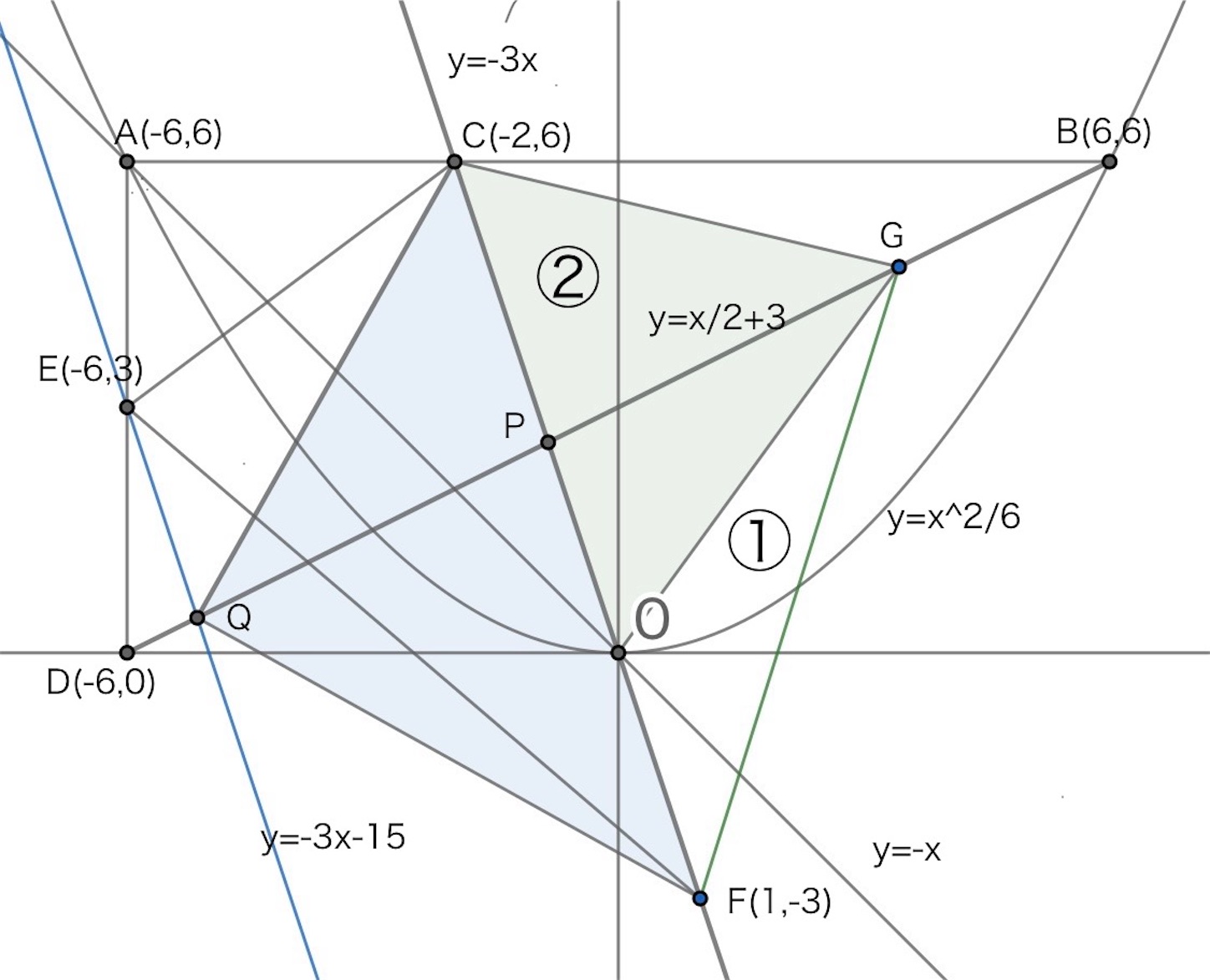
問4 (ウ) も普通は等積変形を使って解く図形的な問題である.

【解】
(ウ) 下図のように, を通り,
と平行な直線を引き
と等積な
を得る (
は直線
上の点でもある).
だから,
と
は等積である. したがって,
は, 線分
の中点である.
の
座標
は,
を解いて
の
座標
は,
を解いて
の
座標
は,
を解いて
//
※ 問 1 (オ) の球の体積も加えると 30 点程度が図形分野の配点である.
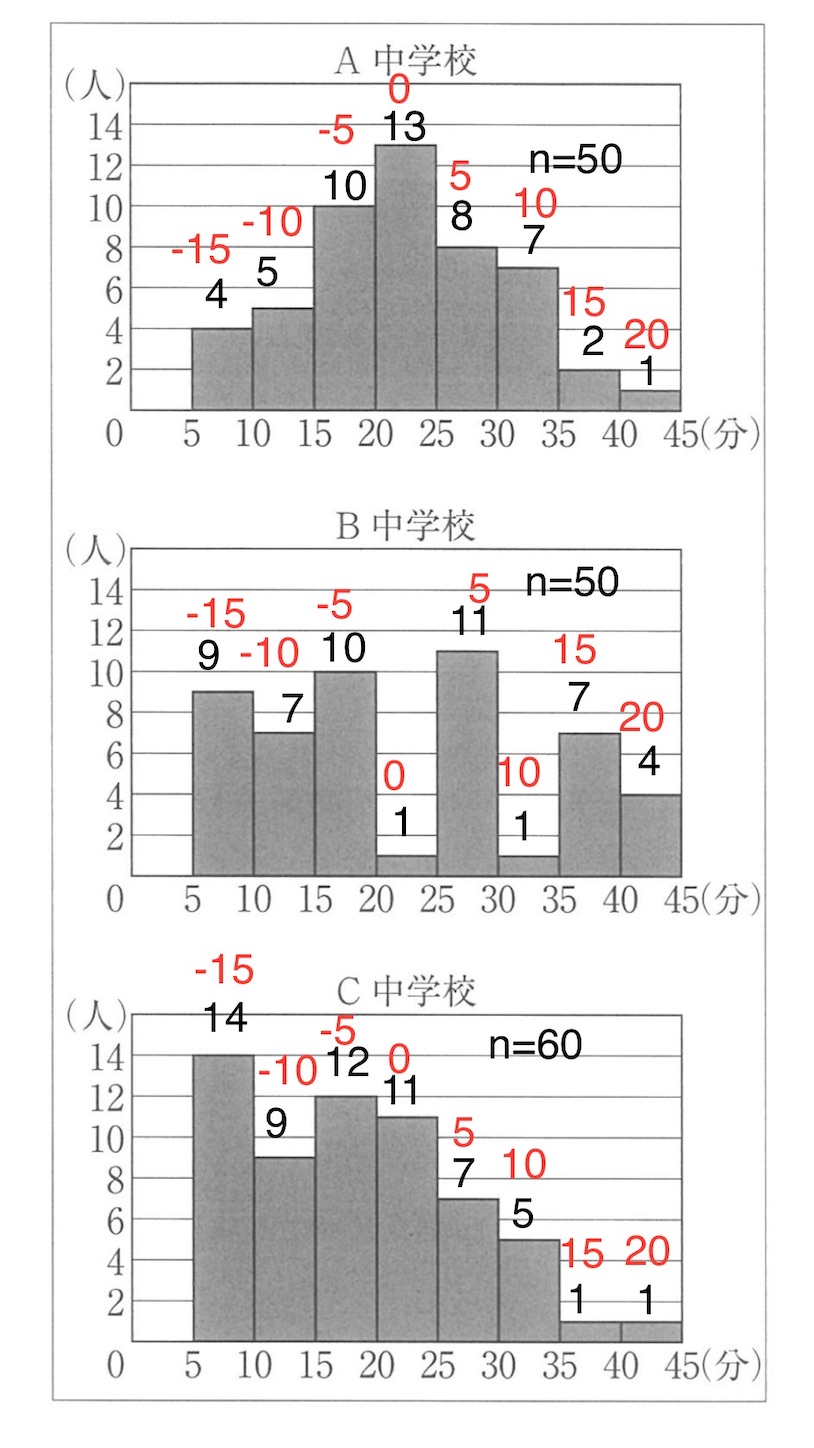
※ データの分析の問題は地道にやればよいのだが, 最後の小問の IV が正しいかどうかだけやっておく.
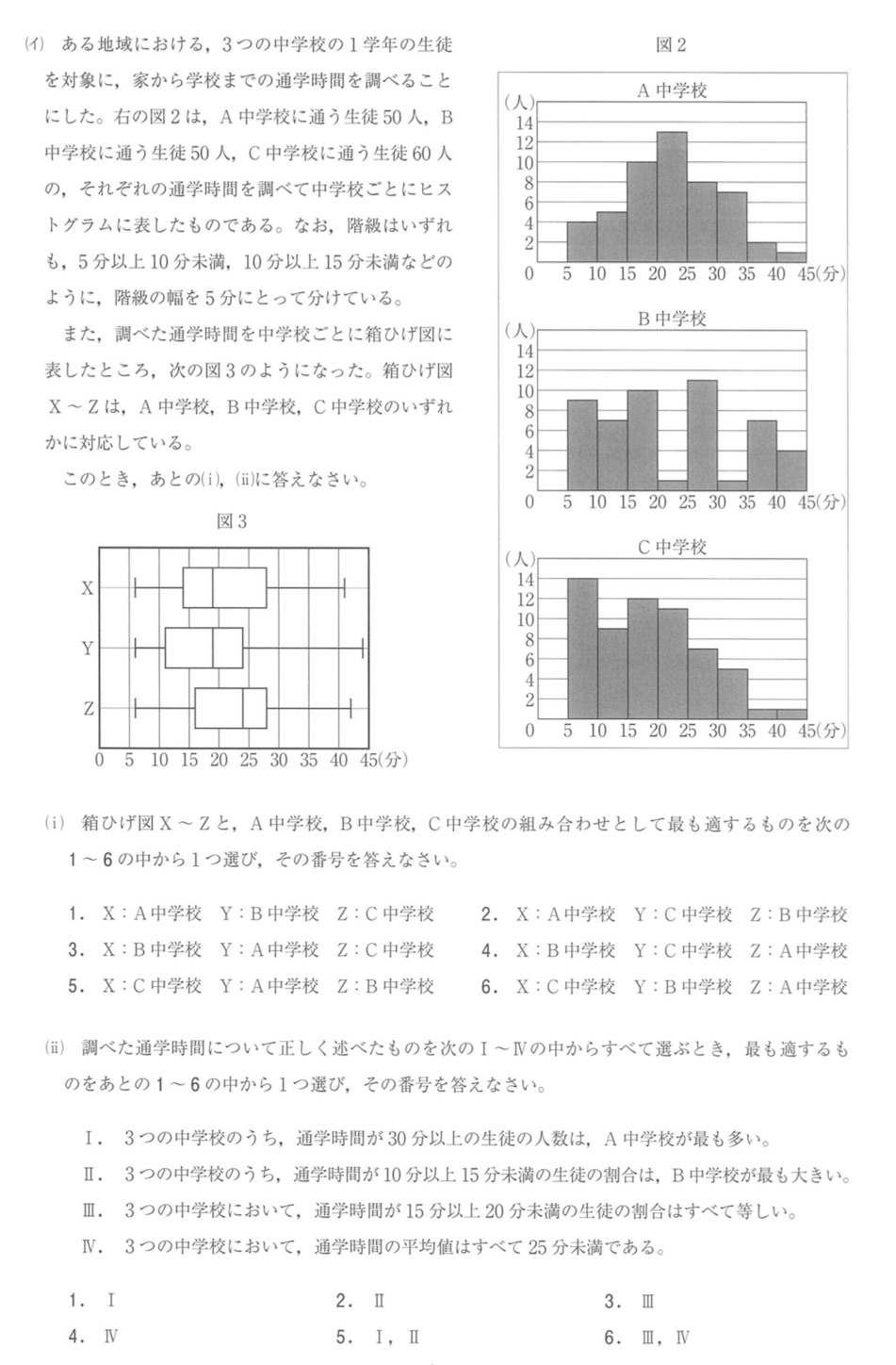
(最後の小問の IV は真か偽か)
平均のとりうる値の上限を調べてみる (任意の階級に属するデータが例外なくその階級の上端の値をとったものと仮定して平均を計算すればよい). 平均の上限を仮に 分とする.
A中学校:
真の平均は 分未満であるといえる.
B 中学校:
真の平均は 分未満であるといえる.
C 中学校:
(実際は計算するまでもないが)
真の平均は 分未満であるといえる.
したがって, IV の主張は正しい.