数 1A の共通テスト問題 (2022 年) の整数解の問題は, 素直に誘導に乗る場合の解を記載していなかったので, ここに一応あげておく. (他の大問も皆そうだが, 小問に順番に答えてゆく過程での「単線的」ともいえる反復構造がこの年の共通テストの大きな特徴である. この問の場合, はともかく
の値を求めるのにも反復的に使える手続きがあったのだと見抜くことは難しい.)
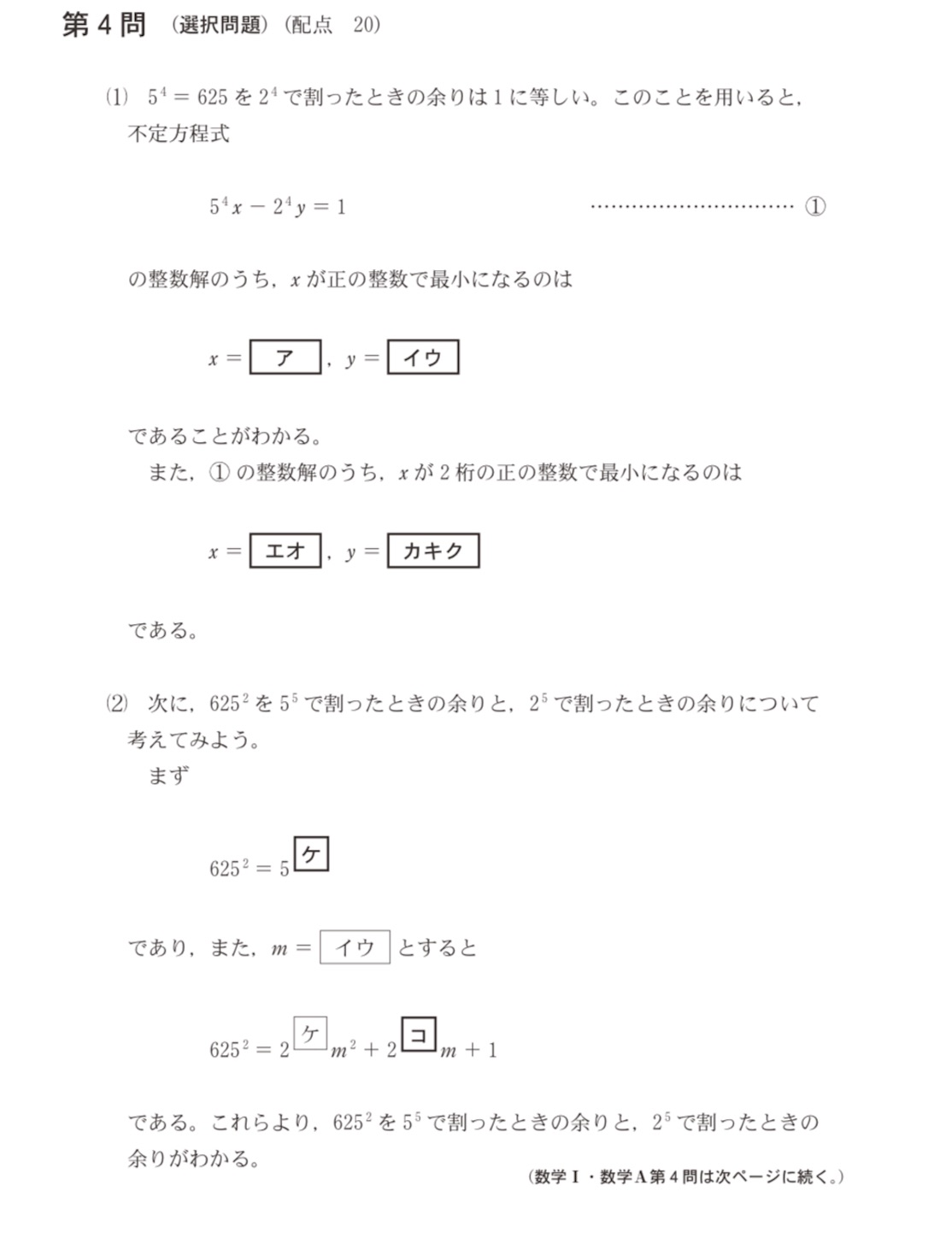
1) を用いると,
から,
の正の整数の最小値は,
.
また, の
桁の正の整数の最小値は,
. このとき, 上の結果から,
を使って,
(2)
(1) から,
だから,
つまり,
//

(3)
から,
(2) の結果
から,
であるが, と
は互いに素であることより,
つまり,
である.
が
桁の正の整数で最小なのは,
このとき, (2) の式を使って
(4)
を用いて, (2) の考察と同様にして,
だから,
と
は互いに素であることより,
の正の整数の最小値は,
. このとき,
から,
を利用して,
より,
したがって,
//
※ を求めるのは単なる計算だから (とそう思うのが落とし穴なのだが……), いろいろなやり方がある. 誘導に乗らないやり方を一つ示せば,
//