陥没地帯 (12)

突然だが、下の問題は 2013 年の京都大学の文理共通の入試問題である。このような線分の長さの比や図形の面積の比を求めさせる類似の問題は高校入試や大学入試の定番ともいえる。もしかしたら中学入試にもあるかもしれない。もちろん、メネラウスの定理やベクトルを使ったってこの種の問題は解けるしそういった解き方を練習しておくのも大事だと思うが、歳をとったせいか、簡単明瞭に解けるものに大仰な定理を適用したり、ごちゃごちゃともってまわった計算の解説を載せる傾向が妙に腹立たしく、解答例を載せる気になった。

【問】
平行四辺形 において、辺 を に内分する点を , 辺 を に内分する点を , 辺 を に内分する点を とする。線分 と線分 の交点を とし、線分 を延長した直線と辺 の交点を とするとき、比 を求めよ。

(解)

まず下の図のように補助線をひく。そうすると色をつけた二つの三角形は相似であり、線分 の長さを とすれば、線分 の長さは となることがすぐにわかる。

下の図の色をつけた二つの三角形も相似だが、線分 の長さは上の基準で である。これで相似比が だということがわかった。

点 を通り、辺 に平行な直線が線分 と交わる点を とする。そうすると、下の図で色をつけた三角形は相似である。 の長さを とすれば、直前に求めた相似比から は である。 は の中点なので は、長さ である。

以上から が答えになる。//

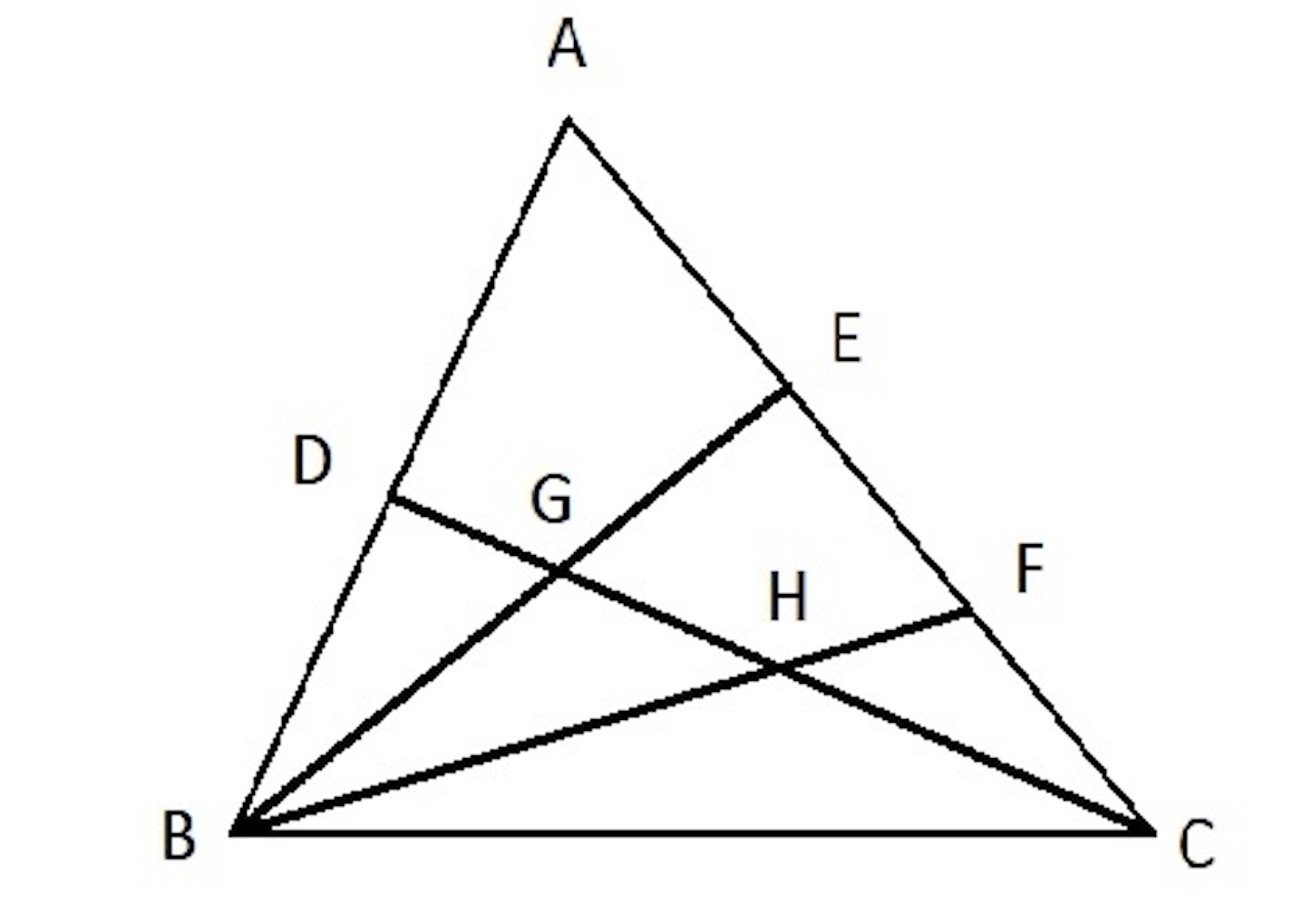
もうひとつ、今度は神奈川県公立高校の2019年入試問題から取りあげてみる。

【問】
三角形 があり、辺 の中点を とする。また辺 を三等分した点のうち、点 に近い点を , 点 に近い点を とする。さらに線分 と線分 の交点を , 線分 と線分 の交点を とする。三角形 の面積を , 四角形 の面積を とするとき、 と の比を最も簡単な整数の比で表しなさい。

(解)

これは次の二つの図で表せば一目瞭然であろう。もちろん、 と は辺 と平行にとる。

これから、

,

であることはすぐに出る。三角形 の面積を とおけば、

である。 は三角形の面積から三角形 の面積を引けばよい。三角形 の面積は であることに注意すると、

以上から、

である。

※ 補助線を , を通り、辺 に平行にひっぱっても同じことのように思えるが、それは , の内分比を求めるには有効である。この問題の場合、この比を求めた方が後の面積計算が幾分楽である。//

※ メネラウスの定理を使うのならば、

から、

から、

これから

//

ムラサキシキブの花。

葉がほとんどないのでなにかと思ったら、リュウノヒゲの花である。

アカメガシワの花。