理系の問題である. いままでの知識で解ける問題だから詳しくは書かない.
ところで, 大正九年に初版が出されて, 百数十版を重ねたという『わかる幾何学』の改訂版を遅まきながら入手した. 改訂版なので当時の趣きがどれほど残っているのか定かではないが, 「緒言」にはこんなことが書いてある.
「殊に幾何学は数学中の暗記物であるから, 問題までも記憶すべきである」
なるほどなあ. やはり秋山武太郎は, わかりやすい嘘は言わない人だ.
【問】

【解】
(1) 問題文の中点云々は, 四面体が等面四面体であることを別の言葉で言っているだけである. 等面四面体は直方体に埋め込まれるから, 直方体の稜の長さを ,
,
とすれば,
をみたす.
から,
,
,
直線 と
のなす角は, 一辺が
と
の長さの長方形の対角線のなす角度であり, 問題文で角度は,
以下の方が指定されているから
つまり
である.
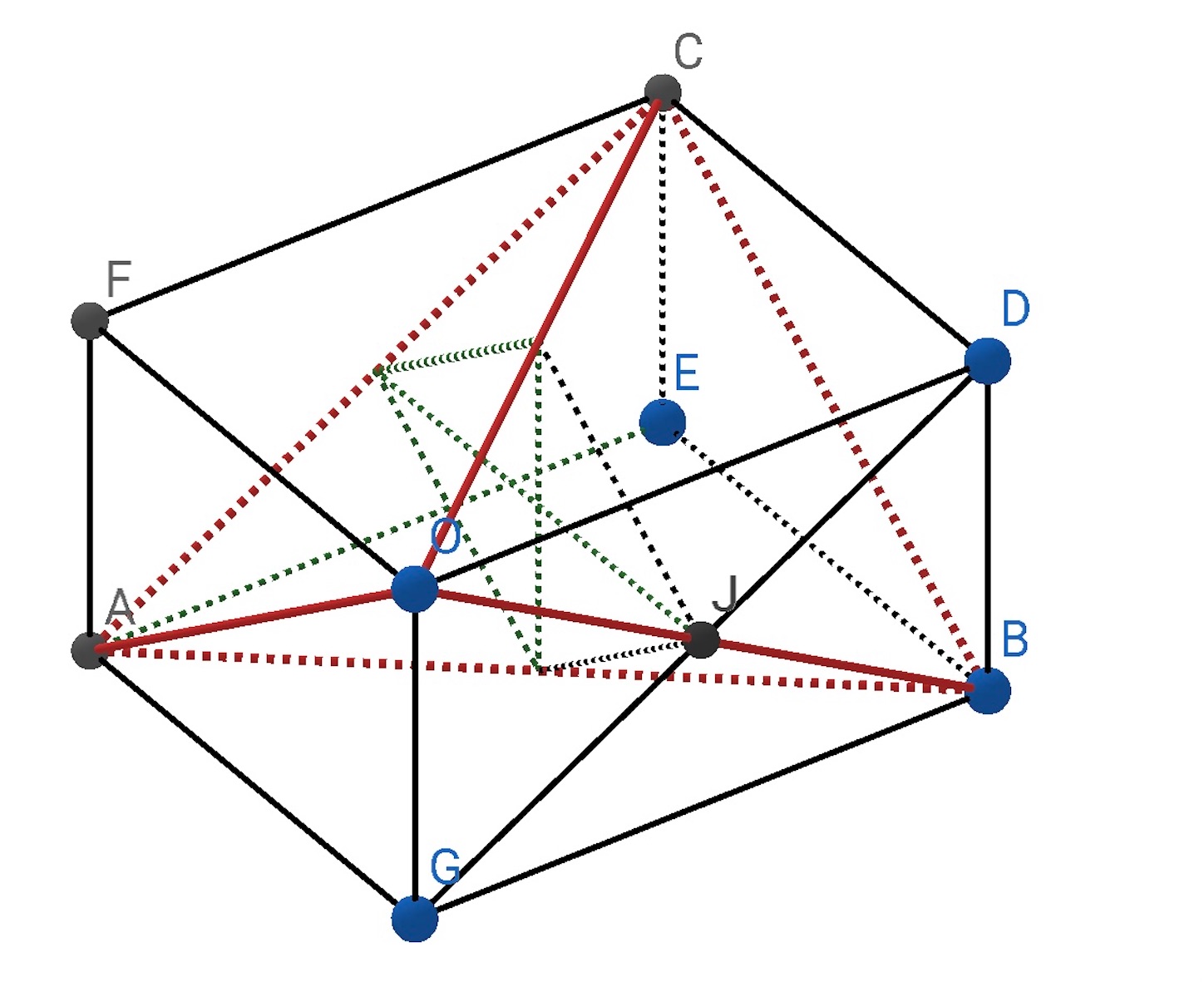
(2) 等面四面体の外心は, それを埋め込む直方体の中心 (対角線の交点) に一致する (重心も内心もそうであった).
したがって,外接球の半径は,
である.//