高校入試問題に戻って, 年度の国立高校入試問題の一部だけやってみた.
立方体の 辺の長さは
cm である.
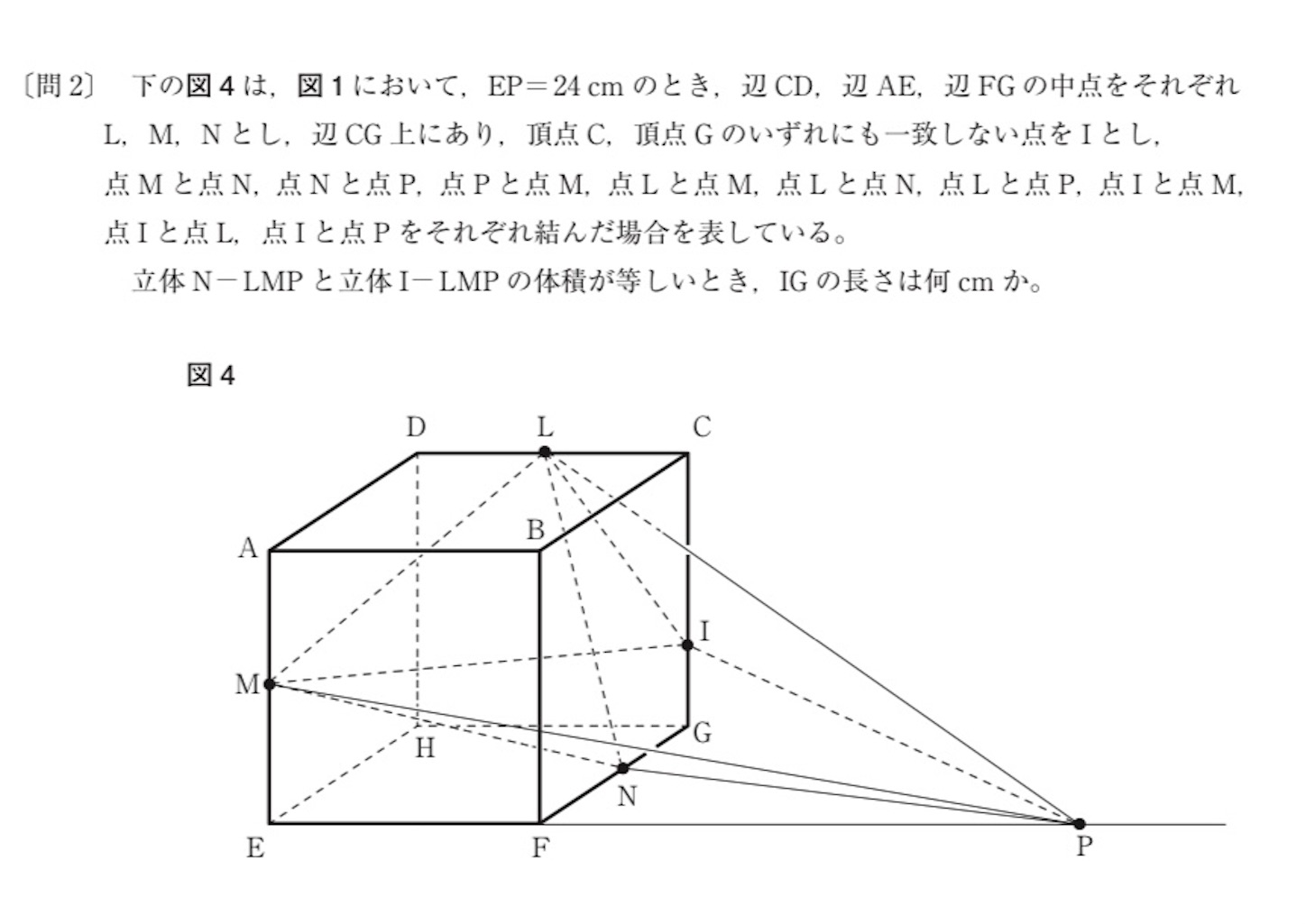
【解】当たり前といえば当たり前なのだが, 「直線と平面が平行である」についてもっとも基本的なことを確認しておく. 直線と平面が平行であることの定義は, 「ひとつの直線とひとつの平面が共有点を持たない」ということである. それで, ここから出てくるもっとも基本的なことは, 「 つの直線が平行ならば, その一つの直線を含みもう一つを含んでいない平面は, 含まれていない直線と平行である」ということである. 簡単だが証明しておく.
直線 ,
を平行な
直線とする.
を含み,
を含んでいない平面を
とする.
と
は平行なので, これをともに含む平面
がただ一つ存在する.
は平面
と
との交線である. つまり平面
と平面
の共有点はすべて
上にある.
と
は平行なので
は
と共有点をもたない. したがって
は平面
と共有点をもたない. つまり
は平面
と平行である.
前置きが長くなったが, 問題の解に入る. 題意を満たすには, 直線 が平面
と平行であればよい. それには, 平面
に含まれている直線と平行であるようにすればよいのだが, 平行線は同一平面にある必要があるので, その同一面を
を含んでいる立方体の面とするのが自然であろう. それで平面
と立方体の面との交線を定める.
わかっている交線上の点は, 下の図で ,
,
である.
と立方体の対面は平行なので, 平面
と立方体の対面の交線は,
を通り
に平行な
である.
と
はともに立方体の面
上にあるから, この面と平面
の交線は,
である. したがって,
を通り
に平行線
を引けば,
は, 平面
に平行となる.
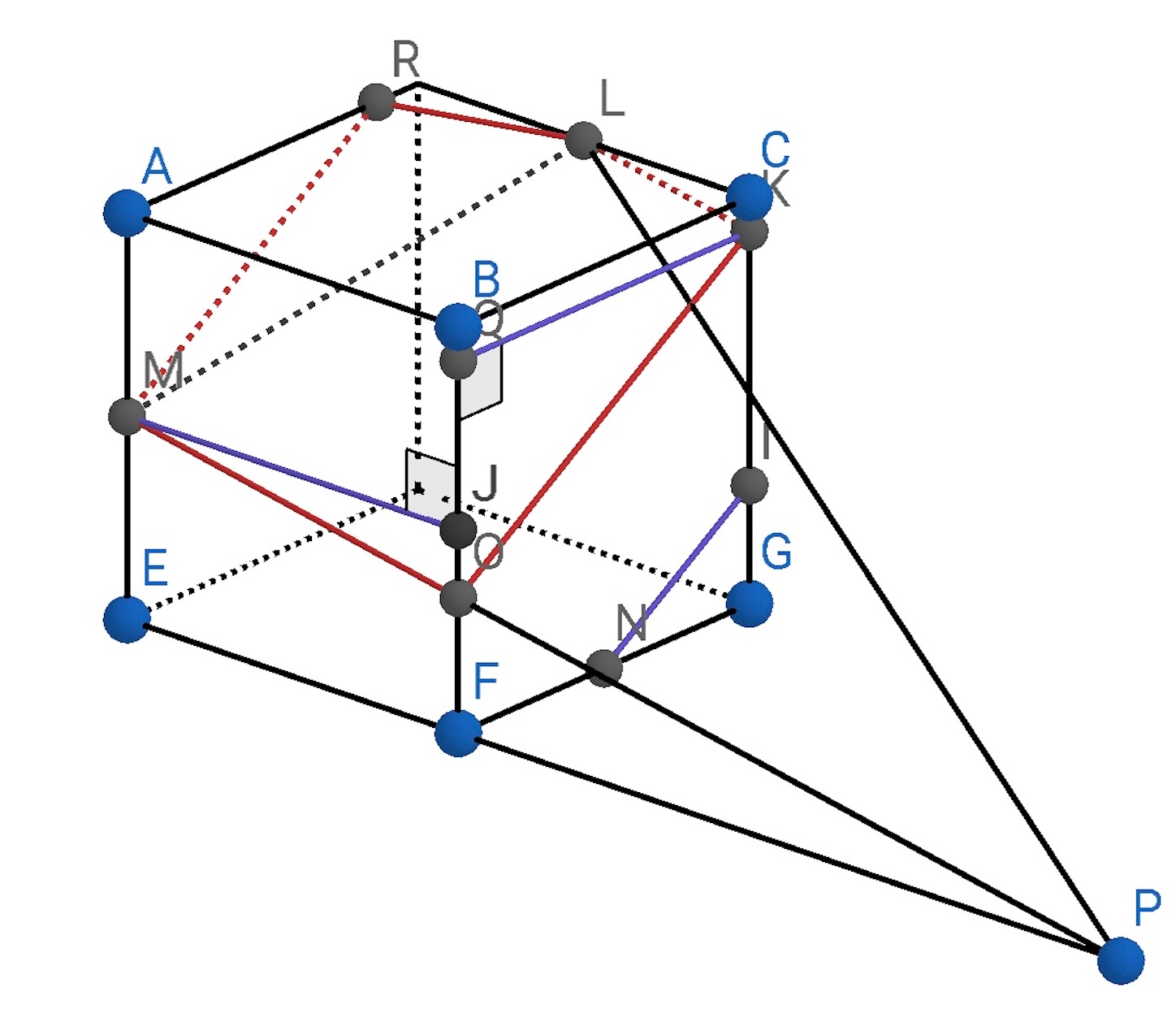
次に の長さを求める.
から,
に垂線を下ろしその足を
とする.
と
は相似だから,
したがって,
は
の対応する辺をそれぞれ平行な辺に写した (正の) 中心相似である. 相似比は
なので,
は
の対応する辺をそれぞれ平行な辺に写した (負の) 中心相似である. 相似比は
なので,
したがって,
(cm)
となる.//