宮澤賢治も詩の中で使っている「ゴーシュ四辺形」とはすべての辺が同一平面上にない四辺形のことである. 下の図で四辺形 はゴーシュ四辺形で, 四辺形の対角線
で分けられる
と
は同一平面にはない.

いま, ゴーシュ四辺形の向かいあった辺 ,
の中点をそれぞれ
,
とする. そしてその二つの中点を通る任意の平面
をとり, 平面
がゴーシュ四辺形の残りの辺,
,
と交る点をそれぞれ,
,
とする. また, ゴーシュ四辺形の頂点
,
,
,
から平面
に下ろした垂線の足をそれぞれ
,
,
,
とする. そうすると
,
は中点であるから,
であることが三角形の合同からすぐにわかる. すると,
であり, このことと三角形の相似より,
であることが言える. つまりゴーシュ四辺形の対辺の中点をすぎる平面は, 残りの 辺を同じ比に分けることがわかった.
これを使って前の記事の問題の別解を与える. 下の図で, 四角錐 と
は底面共通で高さが同じなので体積は等しい.
と
の面積比は,
である. 四面体
と
の高さの比は
である. したがって, 四面体
と
の体積は等しい. 以上から, 平面
は四面体の体積を二等分する.
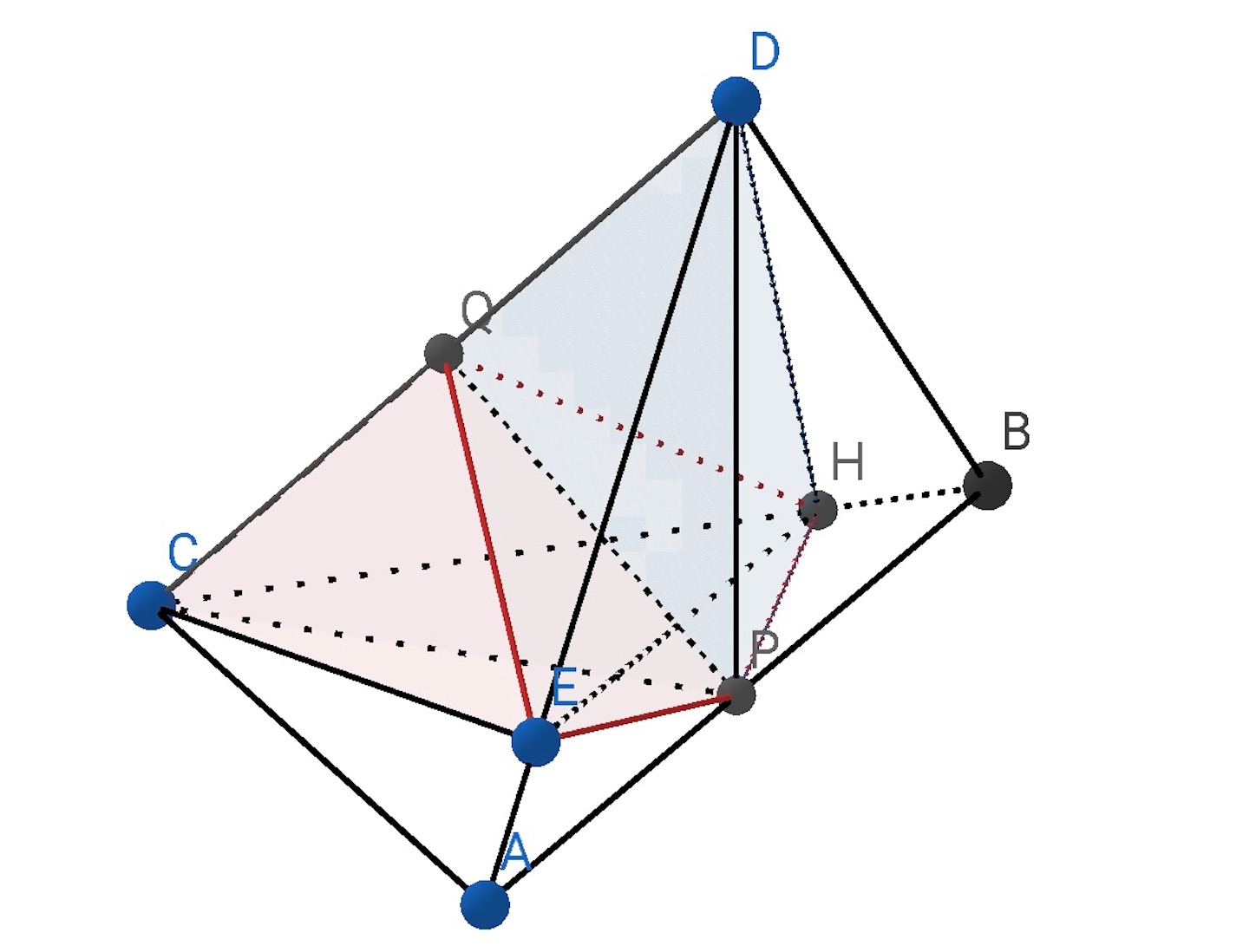
以上からわかるように, 任意の四面体において, 対辺の中点を結んだ直線を含む平面はこの四面体の体積を二等分するのである.
※ 宮澤賢治『心象スケツチ 春と修羅』
「樺太鐵道」より.
山の襞のひとつのかげは
綠靑のゴーシユ四邊形
そのいみじい玲瓏のなかに
からすが飛ぶと見えるのは
一本のごくせいの高いとどまつの
風に削り殘された黑い梢だ