京大入試問題から (4) - ノリの悪い日記

$2018$ 年の文理共通問題. どういう誘導なのかよくわからないまま解いてしまった. $(1)$ の条件があると $(2)$ はもっと簡単に解けるということなのだろうか. $(2)$ を証明するために無駄な条件がある気がする. ただ, 中学の数学で出てくる「平行四辺形の対角線の交点を通る任意の直線はその平行四辺形の面積を二等分する」といった面白さがある.

【解】

(1) 合同な三角形を確認すると,

$\triangle BCD \equiv \triangle ADC$
$\triangle DAB \equiv \triangle CBA$

である. $\triangle QAB$ が二等辺三角形であることを証明する. $\triangle QAC$ と $\triangle QBD$ において, 上の合同より $CA = DB$ , 中点だから, $QC = QD$ , また, 上の合同より, $\angle QCA = \angle QBD$ なので, 二組の辺とその間の角がそれぞれ等しいことより, $\triangle QAC$ と $\triangle QBD$ は合同である. 合同な三角形の対応する辺の長さは等しいので, $QA=QB$ である. したがって, $\triangle QAB$ は二等辺三角形である. $P$ は二等辺三角形 $QAB$ の底辺の中点なので, $PQ$ は $AB$ の垂直二等分線で, $PQ$ は, $AB$ に垂直となる.

$(2)$

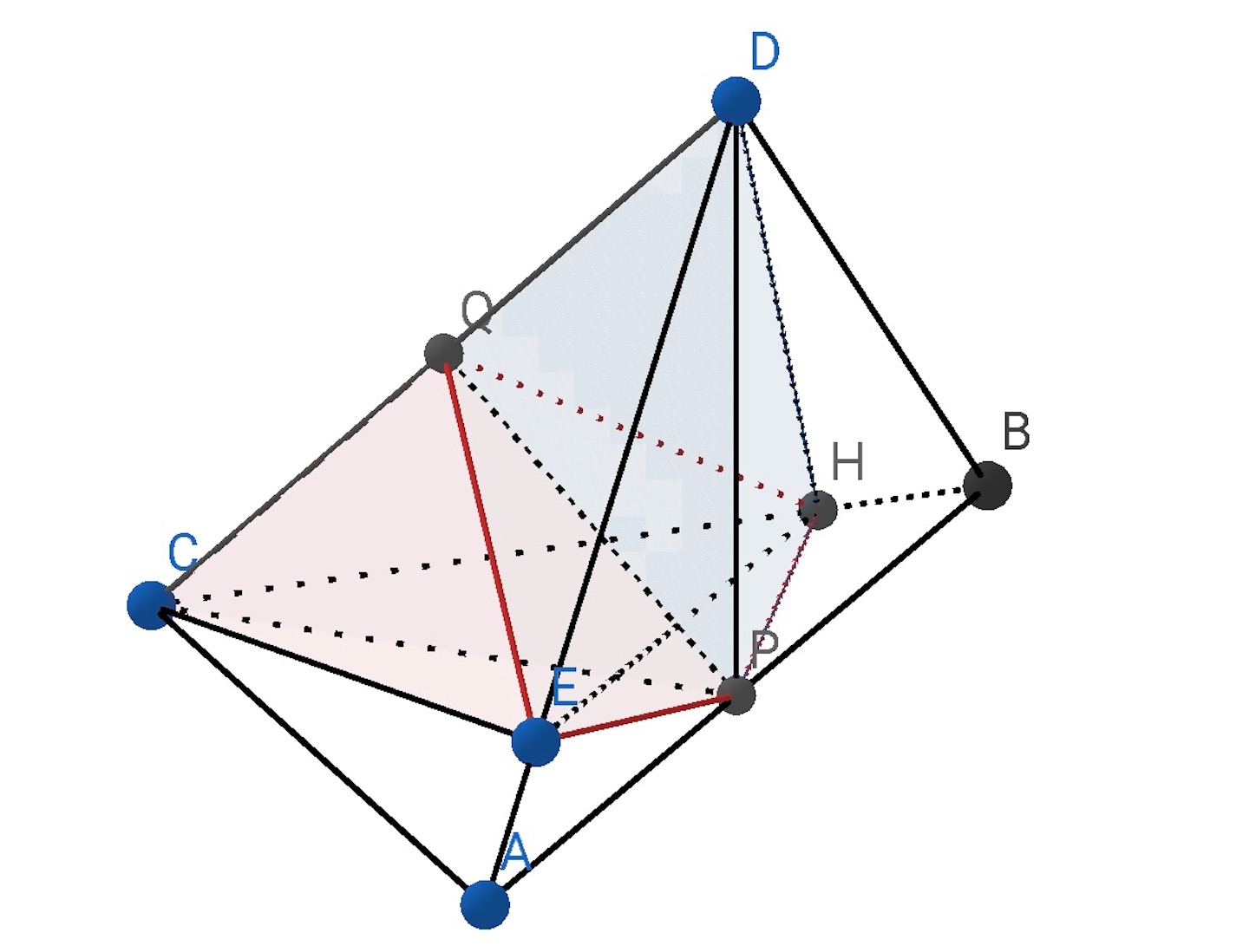
図 (複数載せているが同じ図である) は平面 $\alpha$ が, 四面体の辺 $DA$ , $CB$ を切る場合を作図している. 平面 $\alpha$ が四面体の辺 $CA$ , $BD$ を切る場合も以下の証明は同様にできる.

まず, 平面 $\alpha$ が四面体を切った切断面 $QEPH$ が対角線 $PQ$ によってその面積が二等分されることを示す. そのために, 「 $3$ つの平行平面は, これに交わるどんな直線も同じ比に分ける」という空間図形の基本定理を使う. 以前やったように四面体のねじれの位置にある辺 $DA$ と $CB$ をそれぞれ含む平行平面を考える. その二つの平行平面のちょうど中間に (二つの平面からそれぞれ同じ距離になるよう) 第 $3$ の平行平面を作る. そうするとその $3$ つの平面に交る任意の直線は, その $3$ つの平面の間で $1:1$ の比に分けられる. 直線 $CD$ と直線 $AB$ はこれらの平面を貫いている. したがって, 中点 (ひとつしかないのだった) である $P$ , $Q$ は第 $3$ の平面上にある. また $PQ$ もこの平面上にある. すると, $EH$ と $PQ$ の交点は, $EH$ の中点である. したがって $\triangle QEP$ と $\triangle QHP$ の面積比は $1:1$ である. 以上より, 平面 $\alpha$ が四面体を切った切断面 $QEPH$ が対角線 $PQ$ によってその面積が二等分されることが示された.

次に四面体 $C-QEP$ と四面体 $D-QPH$ の体積は等しいことを示す. なぜなら, 直前の結果より二つの四面体の底面積は等しい. また $Q$ は $CD$ の中点なので四面体の高さも等しいからである. (これは頂点から底面に垂線を下ろし合同を考えればすぐにわかることである. $CQ$ , $DQ$ は合同な直角三角形の斜辺に相当する.) 以上から, 四面体 $C-QEP$ と四面体 $D-QPH$ の体積は等しいことが分かった.

最後に, 平面 $DCP$ は明らかに四面体 $D-ABC$ を右半分と左半分に二等分するが, 平面 $\alpha$ で分割された部分の $C-QPH$ のブロックと $D-QEP$ のブロックを交換すれば (体積は変わることはない), 平面 $DCP$ で分割された右半分と左半分の体積と同じになる. したがって, $\alpha$ で分割された二つの部分の体積は等しい.

※ もしかしたら $(1)$ の誘導は交換したブロックが体積が同じだけでなく, 抜いた場所にビッタリハマることを証明させたかったのかもしれない (出題者は積木マニア?). そこまではつきあってられないなあ.