年の京大入試問題 (文理共通) に次のような問題がある.

この問題はただ解くだけだとつまらない.
『バン () の定理』と呼ばれ「四面体のすべての面の面積が等しくなるのは等面四面体に限る」という内容の典雅な定理がある. もし, この定理を認めるならば京大の入試問題は非常に簡単である.
つの面の面積が等しい四面体は,
つの面の三角形がすべて合同な四面体, つまり等面四面体である. 等面四面体は直方体に埋め込まれるのだった. 一方, ねじれの位置にある辺がすべての組で互いに垂直な四面体を埋め込む平行六面体の面はひし形である. 両方を満足するのは立方体しかない. 立方体に埋め込まれる四面体は正四面体である.
すべての四面体はその内側に球を内接させることができる (ここでは証明せずに認めることにする). 内接球は, 四面体の各面に一点で接している. 内接球の中心を四面体の内心という. 下の図は, 四面体の展開図で, ,
,
,
は内接球とそれぞれの面の接点であるとする. 四面体のひとつの頂点から球の接点までの距離はどこに接線を引いても等しい. したがって, たとえば
と
は三辺がそれぞれ等しいことから合同である. したがって,
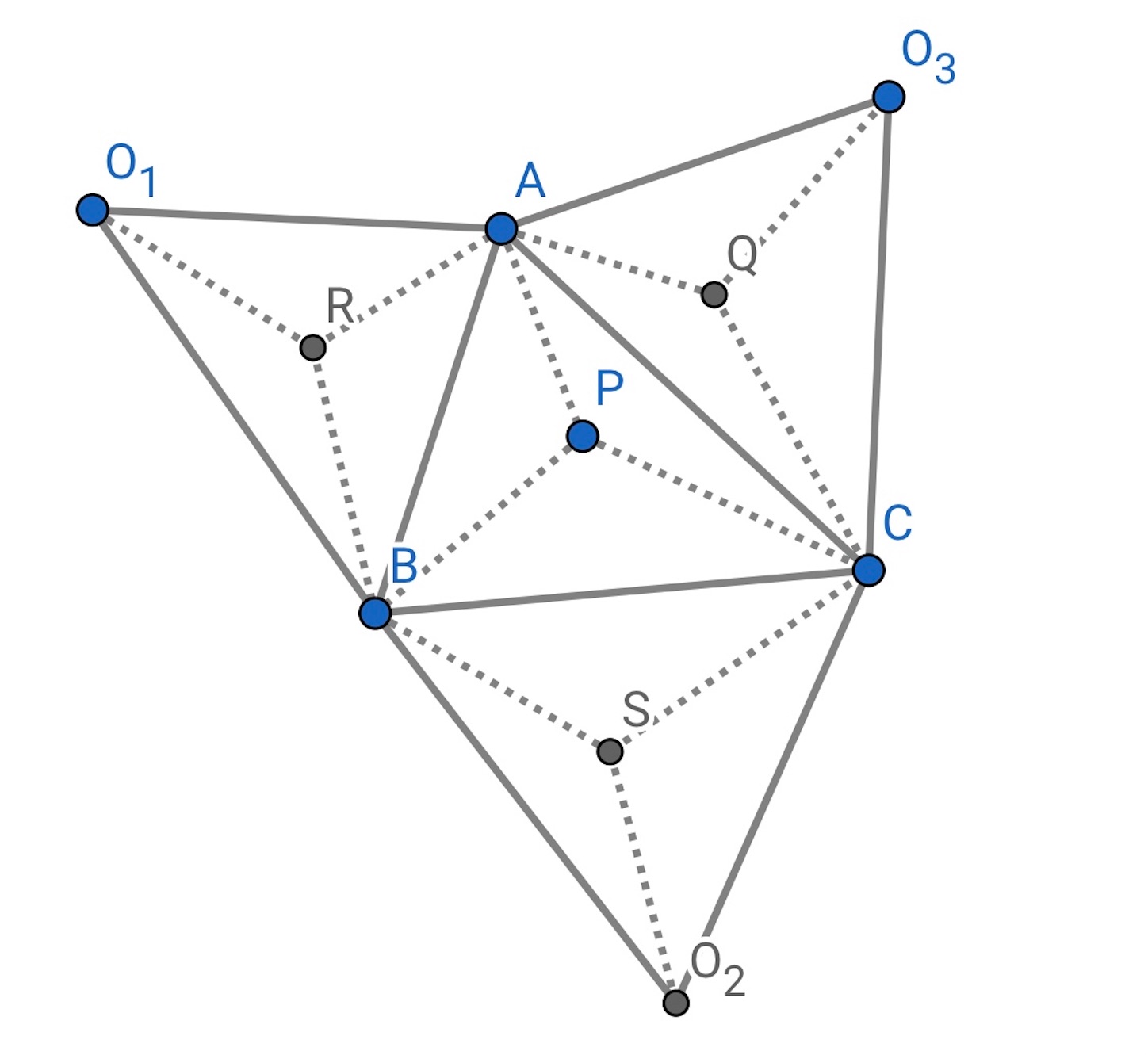
以下同様に, 角に下のように記号 から
までをつける. すると,
前半の 式から,
後半の 式から
したがって
以下, ,
となる. つまり各面の接点に集まる線分によってできる
つの角度はそれぞれ同じになる.
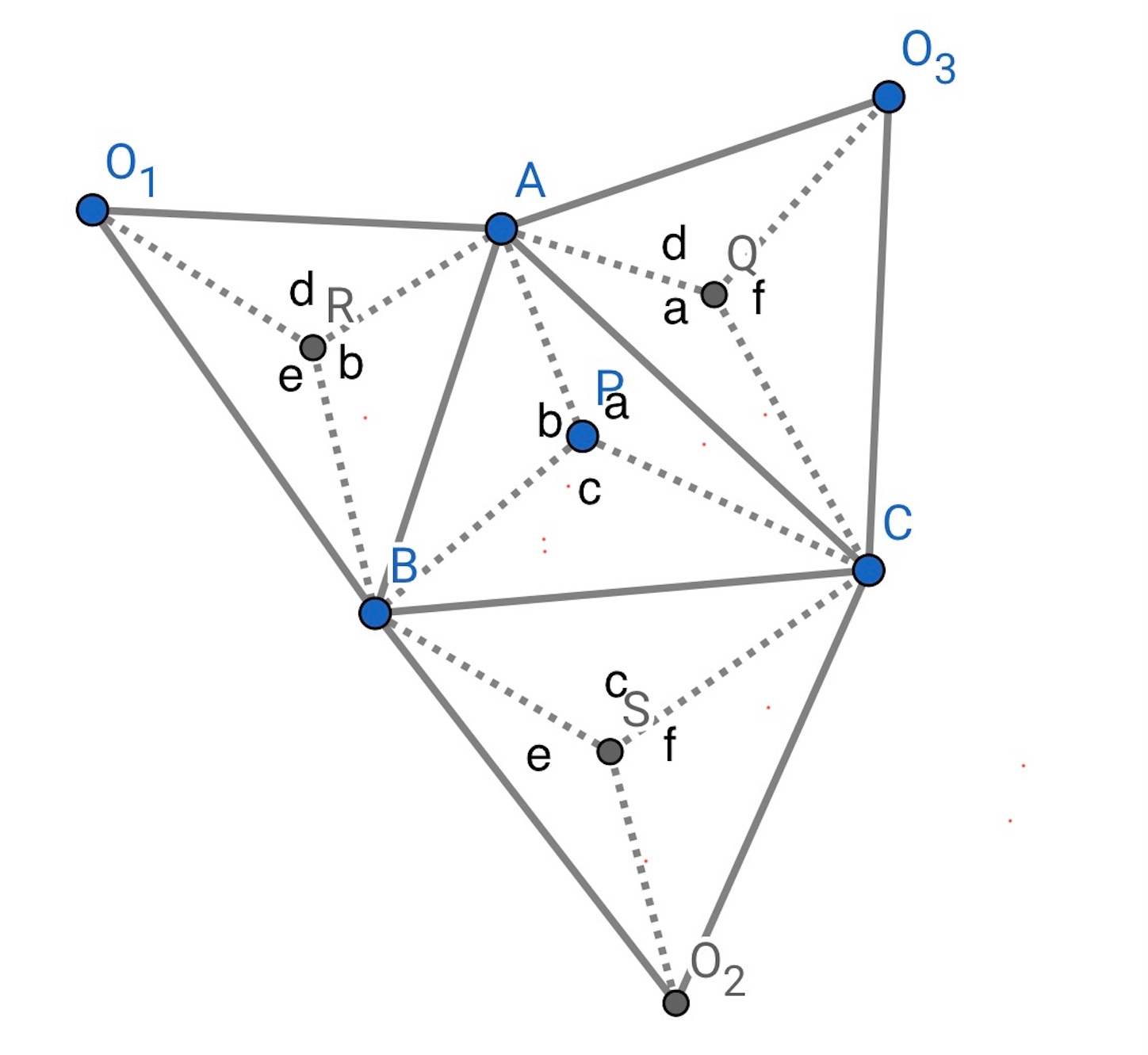
次に四面体の各面の面積がみな等しいとする. 記号 から
を今度は小三角形の面積だと読み換えることにする. すると, 前と同様にして,
,
,
がいえる.
三角形の面積の公式 ( ) と, 上の二つのことから,
が成り立ち,
から
より
となる. これから ,
となり, 結局,
である ( と
から垂線をたてれば, 内接球の中心を通るので, 等面四面体では外心と内心も一致するのだ. なお直方体に埋め込まれることから重心と外心も一致している).
以上のようにすれば, 四面体の各面の小三角形はそれぞれ合同であり, これから四面体の向かいあった辺の長さは等しいことがわかる. すなわち, 四面体は等面四面体である. 逆は明らかなので, の定理が証明できた.