年の問題である.
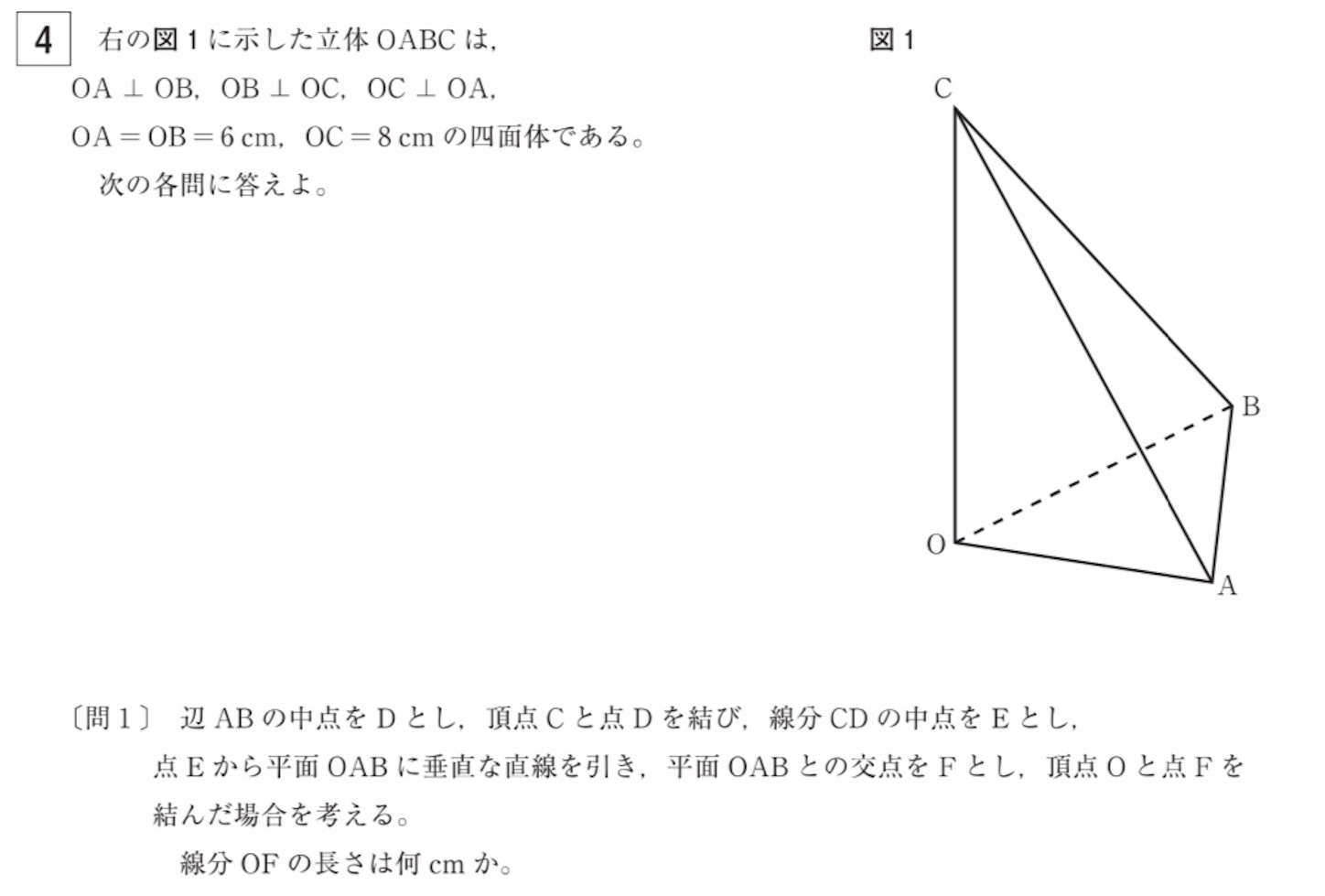
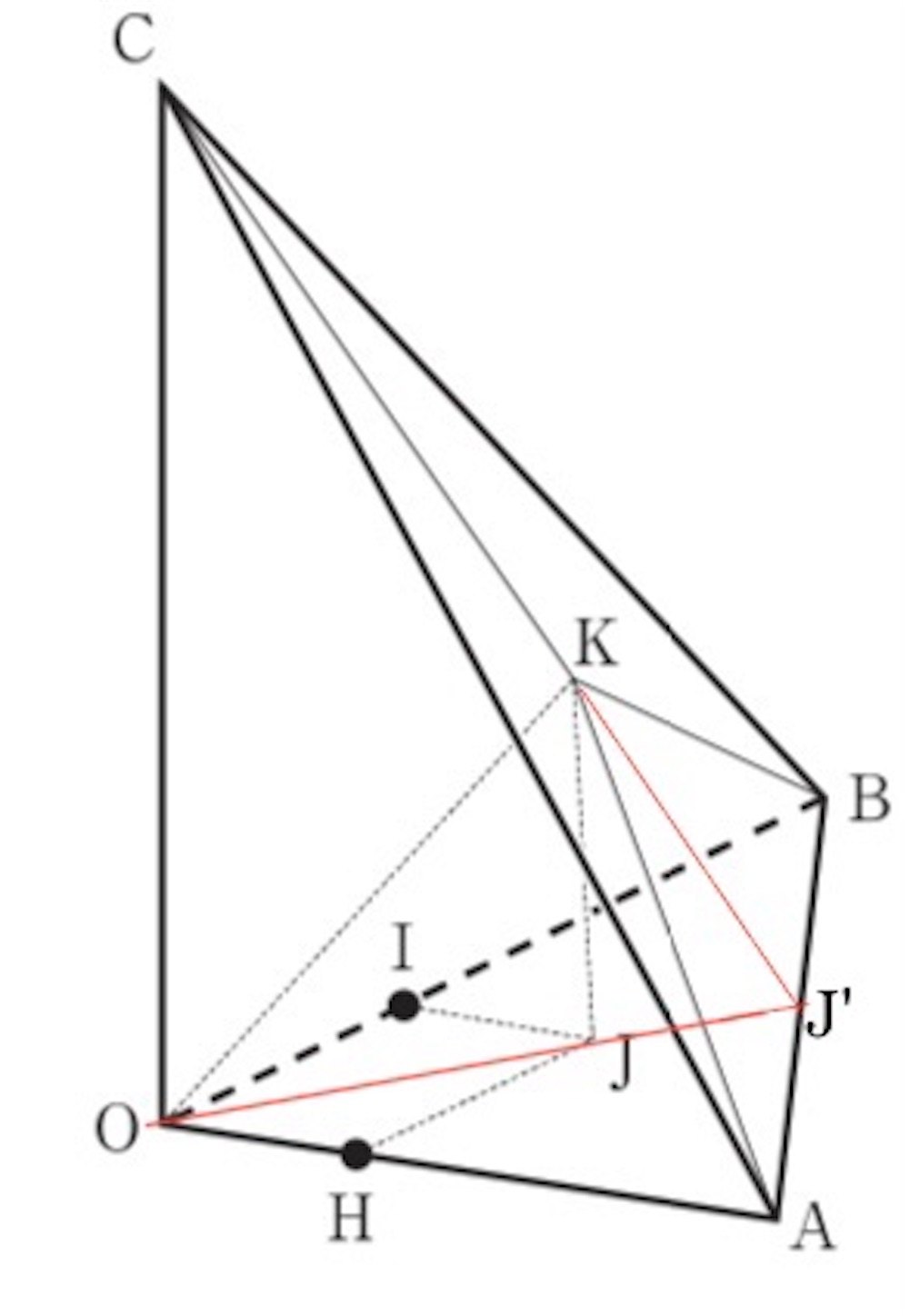
で,
は
の外心だから,
である. 中点連結定理より,
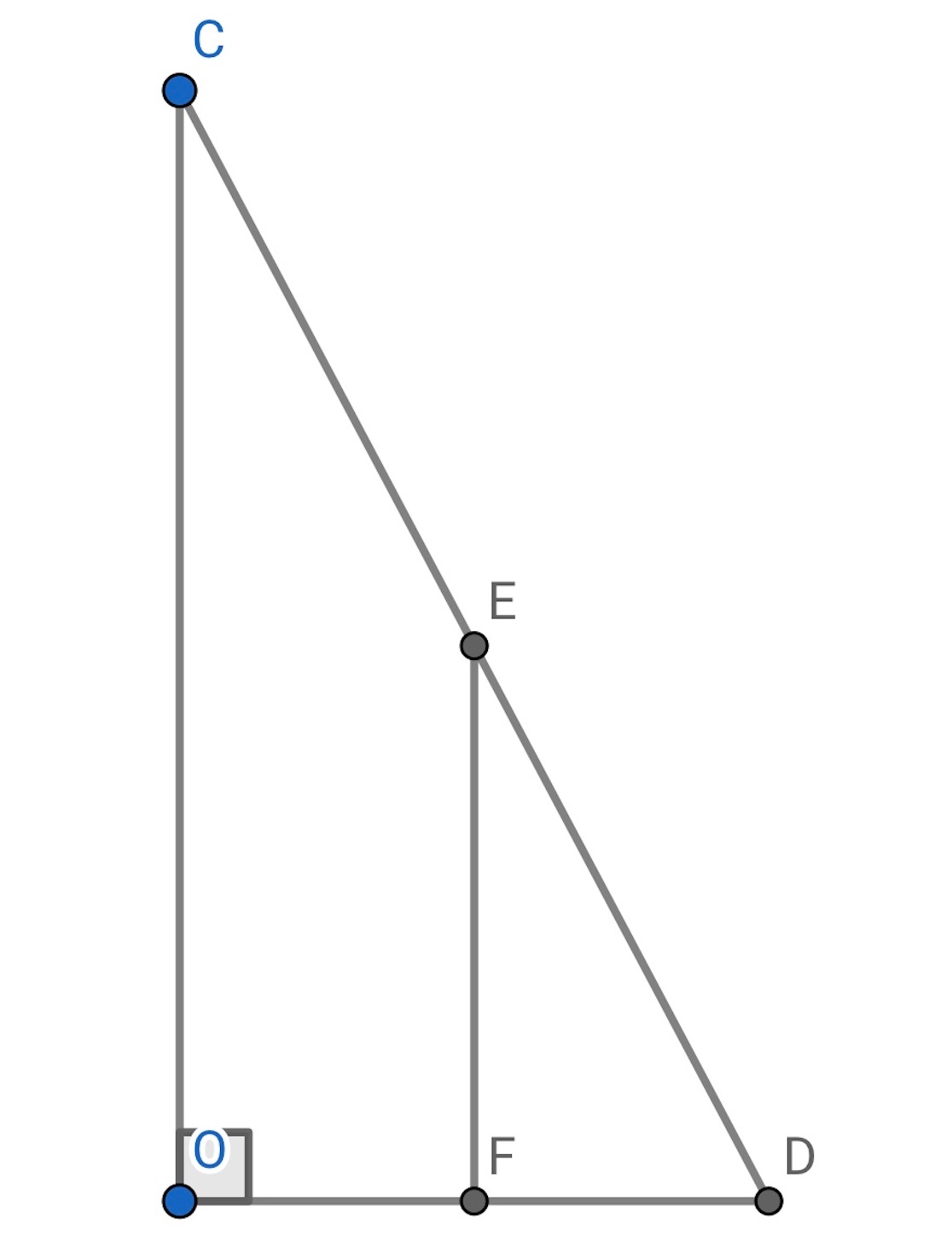
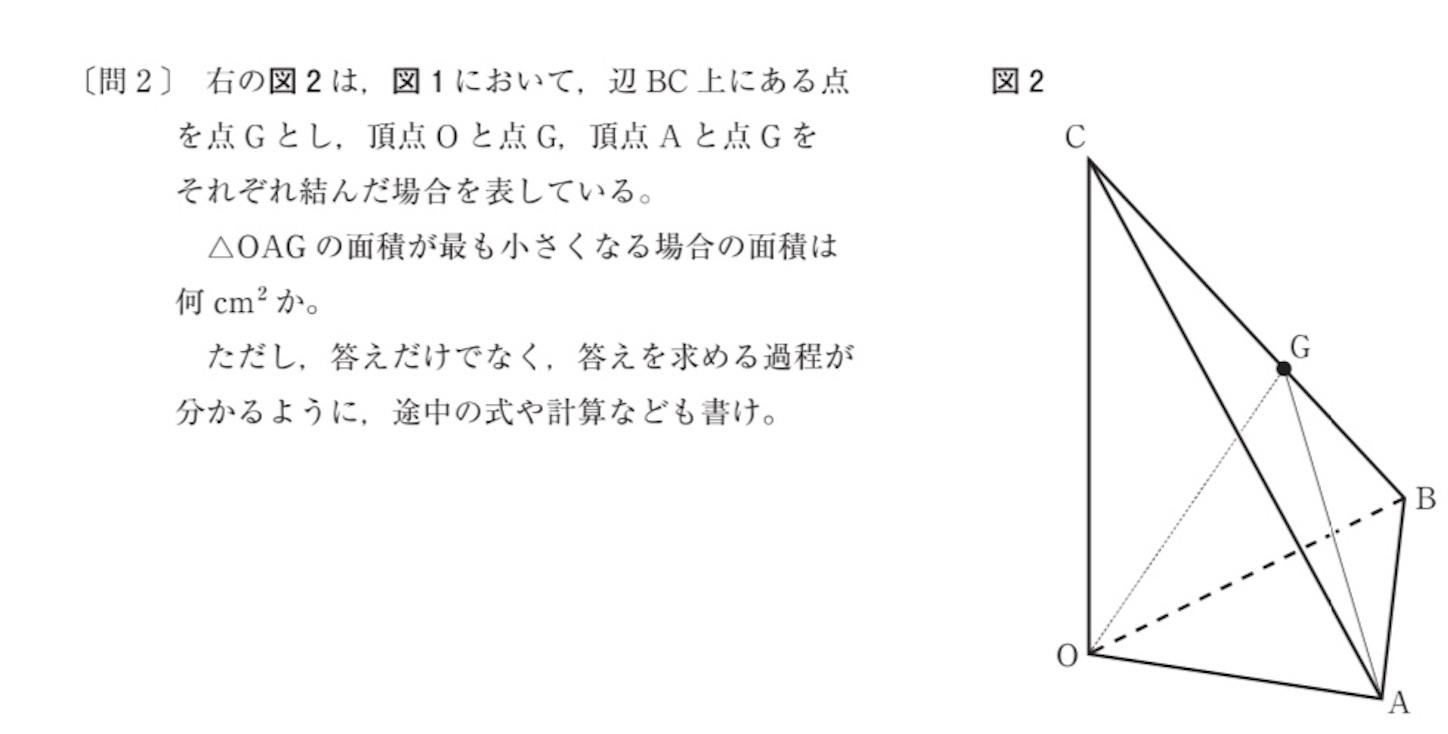
は,
とも
とも垂直なので,
は平面
と垂直である. したがって,
は常に
である. このことから,
の面積が最小になるのは,
の長さが最小となるときであることがわかる. そして, それは
が
と垂直のときである. なぜなら,
が
上の他の位置にあるとき, その点を
とすれば,
は, 直角三角形となるが, 直角三角形の最大辺は直角の対辺である斜辺
となるからである (他の
角は鋭角である).
より,
したがって,
となる.
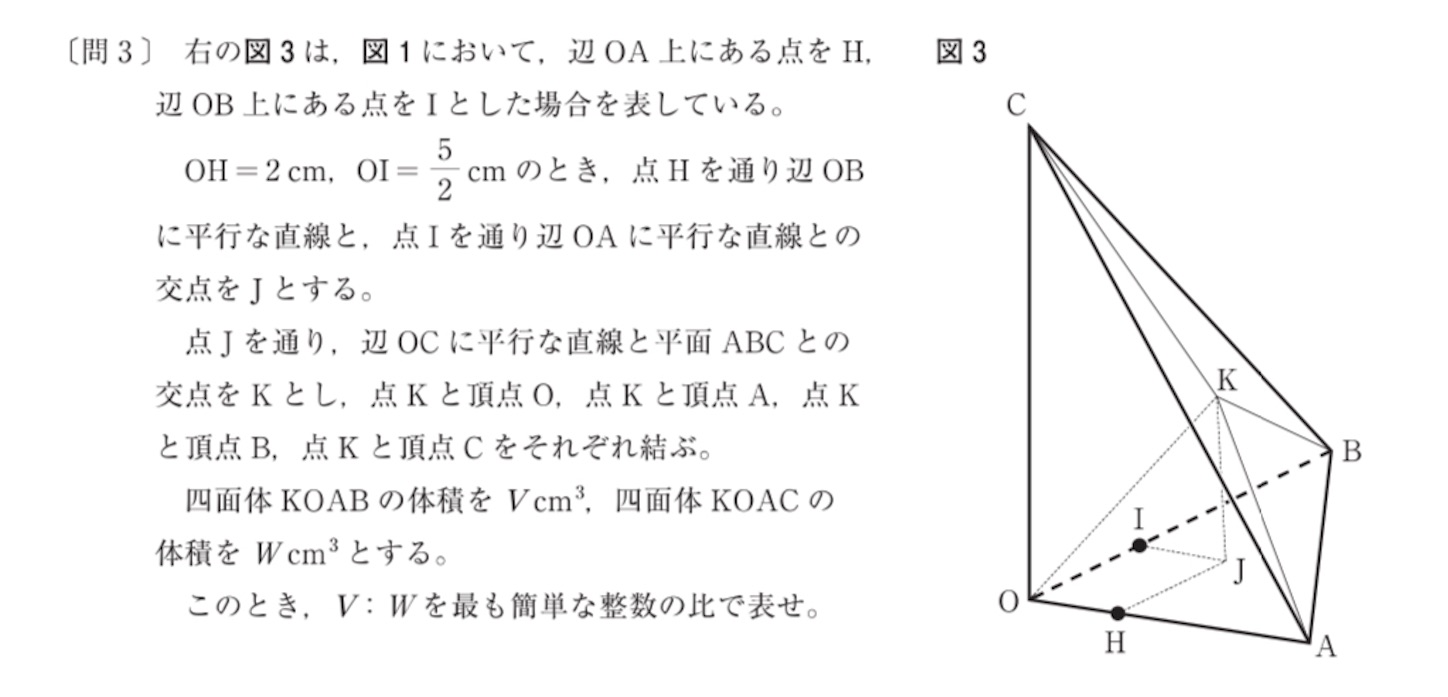
下の図のように, を相似の中心として,
が
上の点
の位置にくるよう相似変換する (そのためには,
と
,
と
がそれぞれ平行であるように作図すればよい).
だから,
である. したがって,
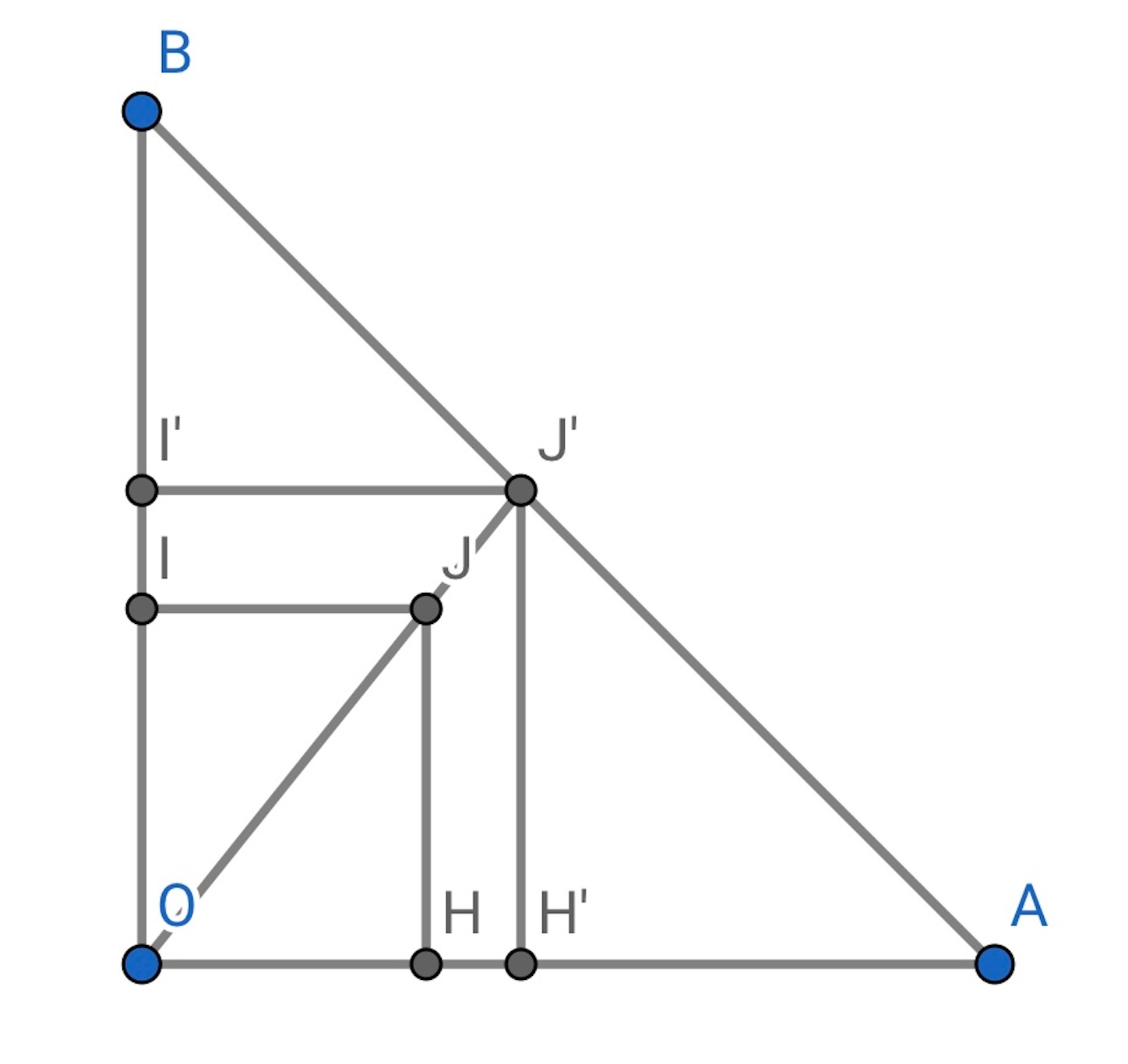
平面 と平面
の交線は,
であり,
はこの線上の点である.
は,
と平行だから,
したがって,
である. これから,
は平面
に平行だから,
から平面
に下ろした垂線の長さは
である.
以上より,
となる. //