ノリの悪い日記

古今東西の映画、ポピュラー音楽、その他をいまここに交錯させながら随想します。

大阪府公立高校入試問題から

初等幾何 立体幾何初歩 中学数学

2017 年度の空間図形の問題. 太字にしたところは, 前の記事の垂直条件とともに空間図形の問題を解くときには常に頭においておくべき最低限のものである. なお, 最後の 3) - ② は正答率 0.7 % とある.


【解】
(1)-①
\displaystyle{IH = 4\cdot \frac{8-x}{8} =\frac{8-x}{2}}

(1)-②
\displaystyle{x\left(\frac{8-x}{2} + 4\right) =16}

から,

x^2 -16x + 32 = 0

これを解いて 0 < x < 8 のものをとると,

x = 8 - 4\sqrt{2}

(2)
CH = CG ということだから,

x^2 + 16 = (8-x)^2
8(8-2x) = 16
x = 3

したがって,

GH = \sqrt{4^2 + 2^2} = 2\sqrt{5}
AG = AH = \sqrt{4^2 + 5^2} = \sqrt{41}

GH を底辺としたときの高さは,

\sqrt{41 - 5} = 6

\triangle AGH = 6\sqrt{5}

(3)-①

三角錐 JGHC の体積は,

\displaystyle{ \frac{1}{3}\cdot 12 \cdot 6 = 24 }

また,

JA: JC = 2:6= 1:3

メネラウスの定理より,

\displaystyle{\frac{JK}{KG}\cdot \frac{2}{8}\cdot \frac{4}{2}=1}
\displaystyle{\frac{JK}{KG} = \frac{2}{1}}

したがって,

JK: JG = 2:3

(あるいは, 以下の図のように面積比から線分比を求めるなど, 自分の好きな方法で求めることができる.)

点 J, C, H を含む平面はただひとつ存在する. また, 点 H を通り直線 JC に平行な直線もこの平面に含まれる. 下図のように, その平行線と ED との交点を N とする. 直線 AN はこの平面と平面 ABED の交線であり, L はもちろん, この交線上にある (平面と平面の共有点は一本の直線である). これも当然だが, 直線 AN, JH も同じ平面上にある (平面上の任意の 2 点を通る直線はその平面に含まれる).

\displaystyle{ HN = 4 \times \frac{6}{8} = 3}

で, \triangle LJA と \triangle LHN の相似より,

JL: LH = 2:3

以上より四角錐 JAKL の体積は,

\displaystyle{ 24 \times \frac{1}{3} \times \frac{2}{3}\times \frac{2}{5}= \frac{32}{15}}

\displaystyle{\triangle JKA = 18 \times \frac{2}{3} \times \frac{1}{3} = 4}

したがって,

\displaystyle{ \frac{1}{3} \times 4 \times LM= \frac{32}{15}}

から,

\displaystyle{ LM= \frac{8}{5}}

(3)-②

上の結果から求める体積は,

\displaystyle{ 24 - \frac{32}{15} =\frac{328}{15}}
//

※ LM の長さを直接求めることもできる. 下の図のように直線 LM と点 H により決まる平面を考える. 点 Hを通る直線 LM の平行線はこの平面に含まれる. また, この平行線は CF とも平行で, 平面 BEFC にも含まれる. 平行線と BC との交点を P とする. PM の延長線は, CA の延長線, HL の延長線と J で交わることが, 空間図形の定理 *1よりわかるから, 結局 J, M , L, P, H は同一平面上にある.

三角形の相似より,

MJ: MP = JA: QP = 2:3

なので (この比も, メネラウスの定理を使うなど自分の好きな方法で求めることができる),

\displaystyle{ML = \frac{2}{5}\cdot PH = \frac{8}{5}}

となる.


//

※ 問題文に親切に LM は平面 ABC に垂直と断ってくれているが, CF は, AC, BC に垂直だから, CF は平面 ABC と垂直である. CF は, AD と平行で, LM は, AD に平行なのだから, LM は平面 ABC に垂直である.
//

*1:定理 二つずつ相交わる三つの平面 P, Q, R があって P と Q との交りを a, P とR との交りを b, Q と R との交りを c とするとき, a, b, c の内のいずれか二つが交れば残りの一つもまたその交点を通る.
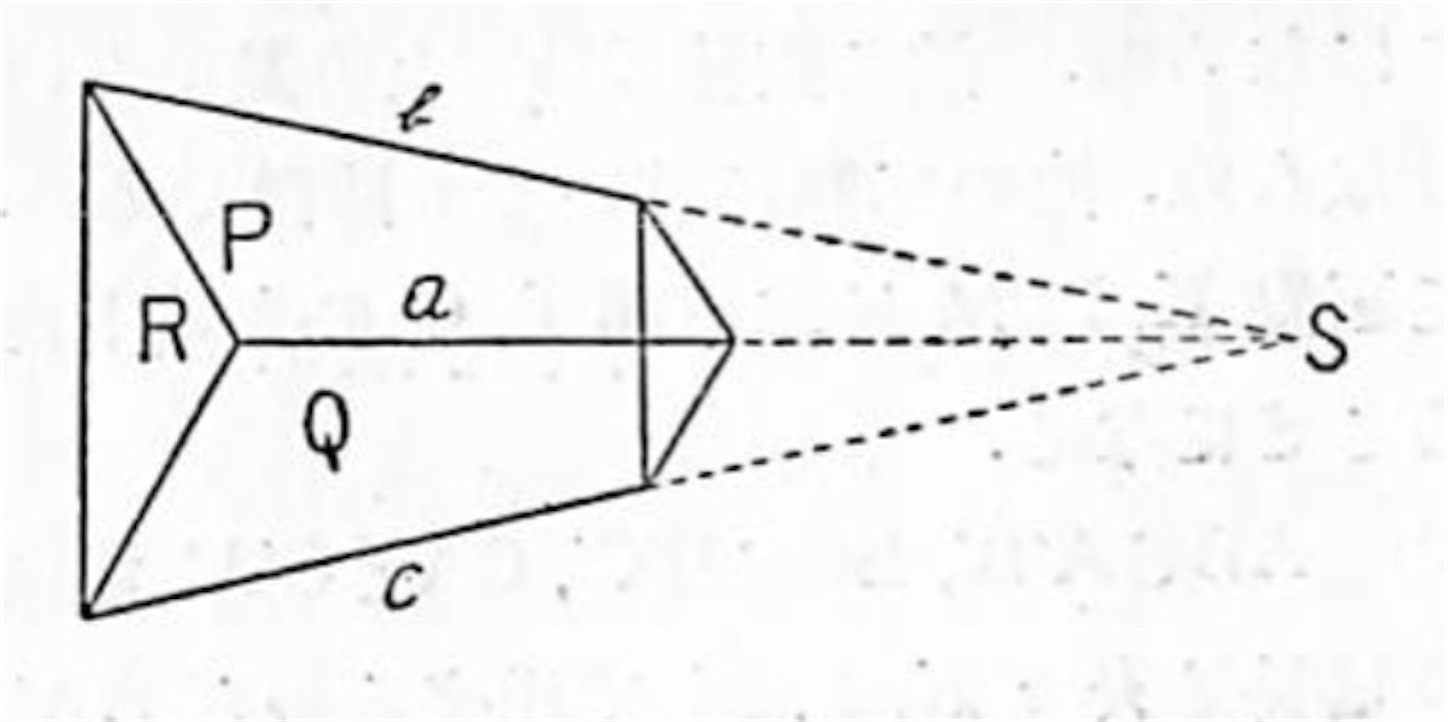
証明: a, b, c の三つの内, 例えば a と b とが相交わると仮定しその交点を S とすれば, S は a の上にあるから a を含む平面 Q の上にある. 同様に S は平面 R の上にもある. 然るに Q と R とは直線 c の他には共有点を持たないから S は c の上になければならぬ. 故に c は S を通る. 即ち a, b, c の内, 何れか二つが交われば残りの一つもまたその交点を通ることが証明された.