京大文系 年のやさしい問題. しかも, 記事
ですでにやった内容だが, いろいろな求め方があるので, 別解としてあげておく. 半角の公式はすぐに忘れるが, 忘れたら都度導出していれば, そのうち自然に覚えてしまう.
【問】

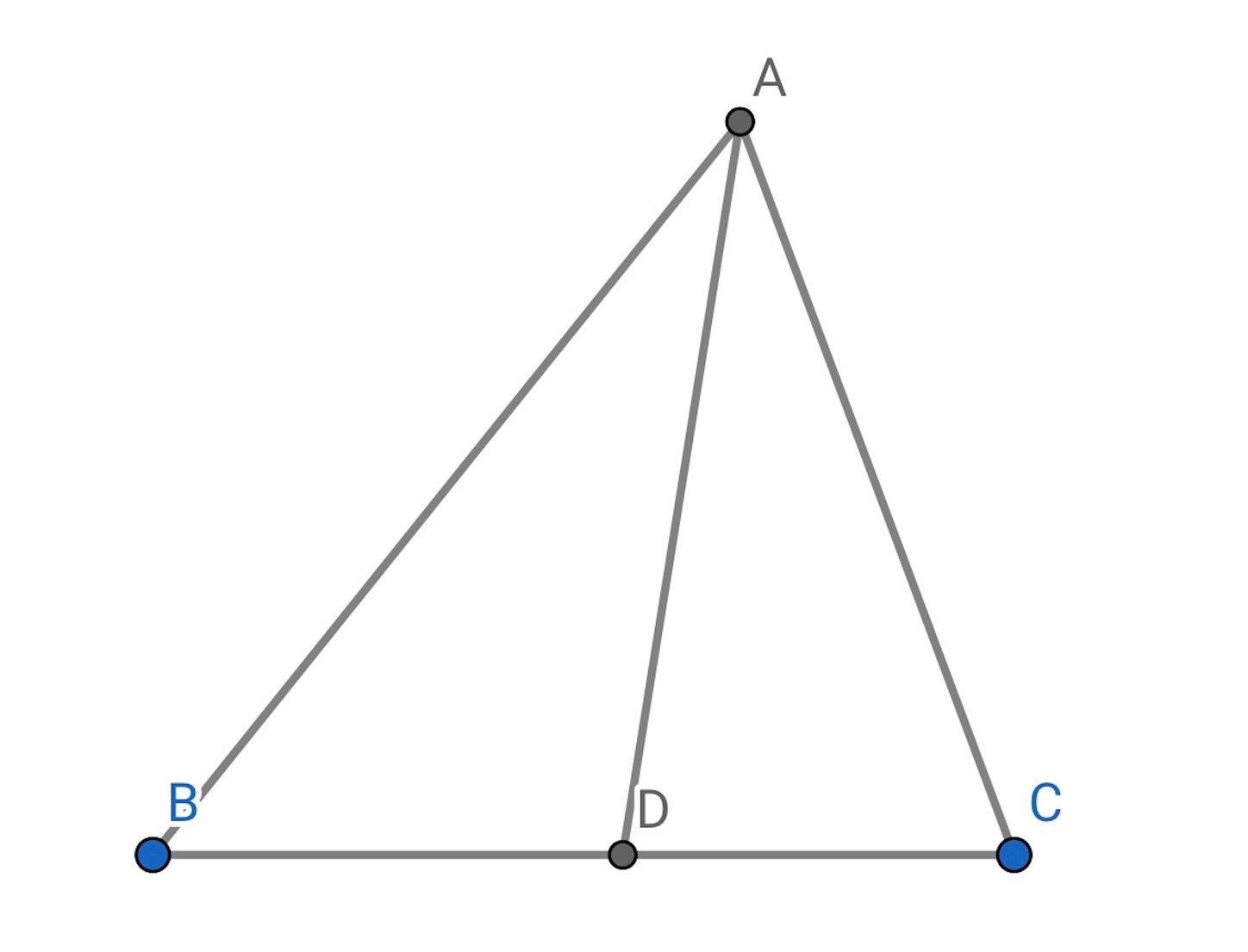
【解】
,
,
とおく.
とすると,
だから,
したがって,
よって,
以上から,
//
※ もっと簡単には,
から,
だから,
でよい. //
京大文系 年のやさしい問題. しかも, 記事
ですでにやった内容だが, いろいろな求め方があるので, 別解としてあげておく. 半角の公式はすぐに忘れるが, 忘れたら都度導出していれば, そのうち自然に覚えてしまう.
【問】


【解】
,
,
とおく.
とすると,
だから,
したがって,
よって,
以上から,
//
※ もっと簡単には,
から,
だから,
でよい. //