三角形の重心と内心が常に三角形の内部にあるというような基本的なことを高校数学の範囲で証明するには, ベクトルを使うのが明快でよいと思う. 例えば,
「 において, 点
が, 直線
に関しては頂点
と同じ側にあり, 直線
に関 しては頂点
と同じ側にあり, 直線
に関しては頂点
と同じ側にあるとき, 点
は
の内部にある」
(「同じ側」とは例えば, 線分 が直線
と交わらないということである.)
といったような三角形の内部の定義から証明するのはしんどい気がする.
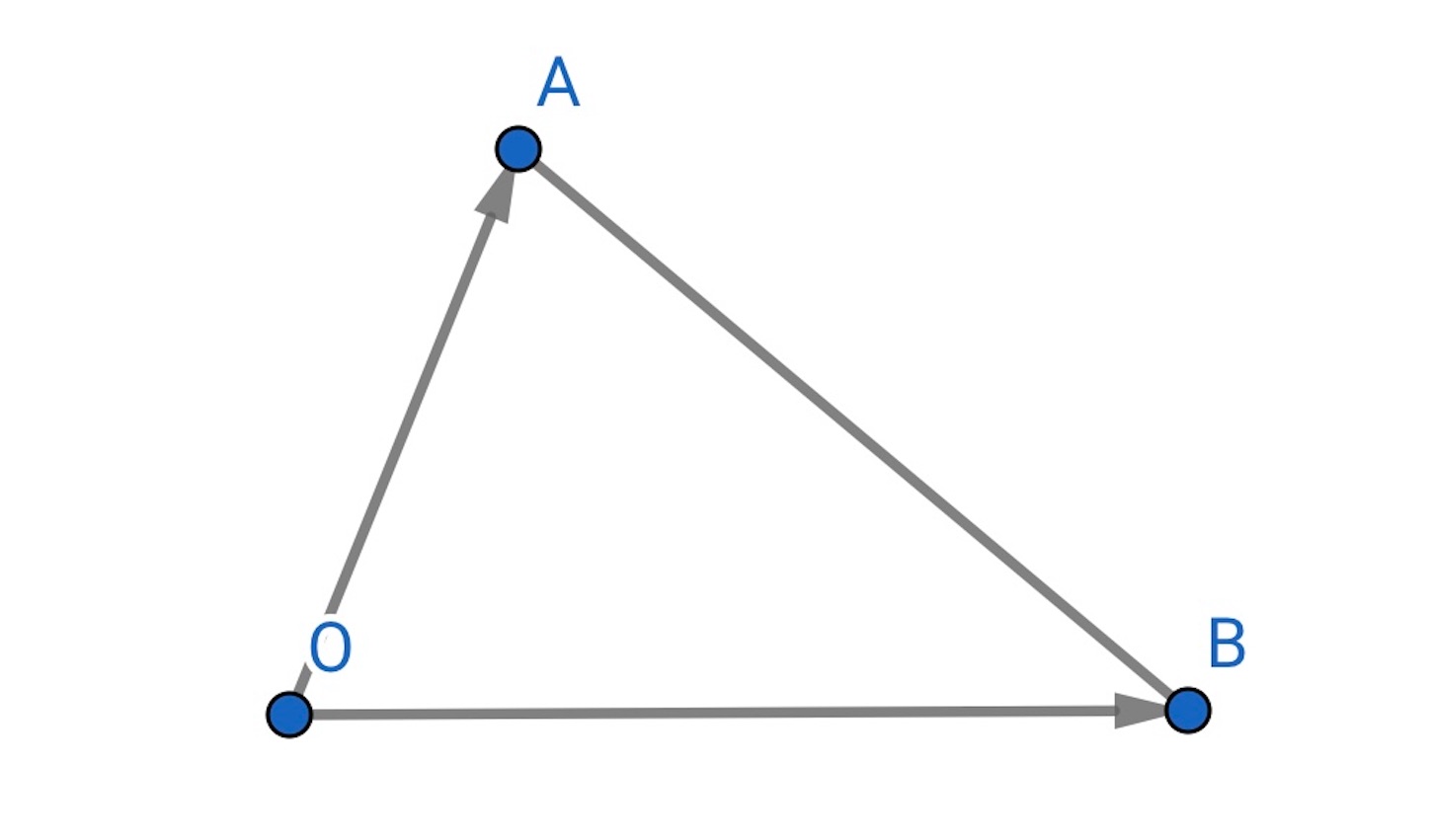
,
とすると, 点 が
の内部にあるための必要十分条件は,
,
,
(,
は実数) だということはすでに学んでいる.
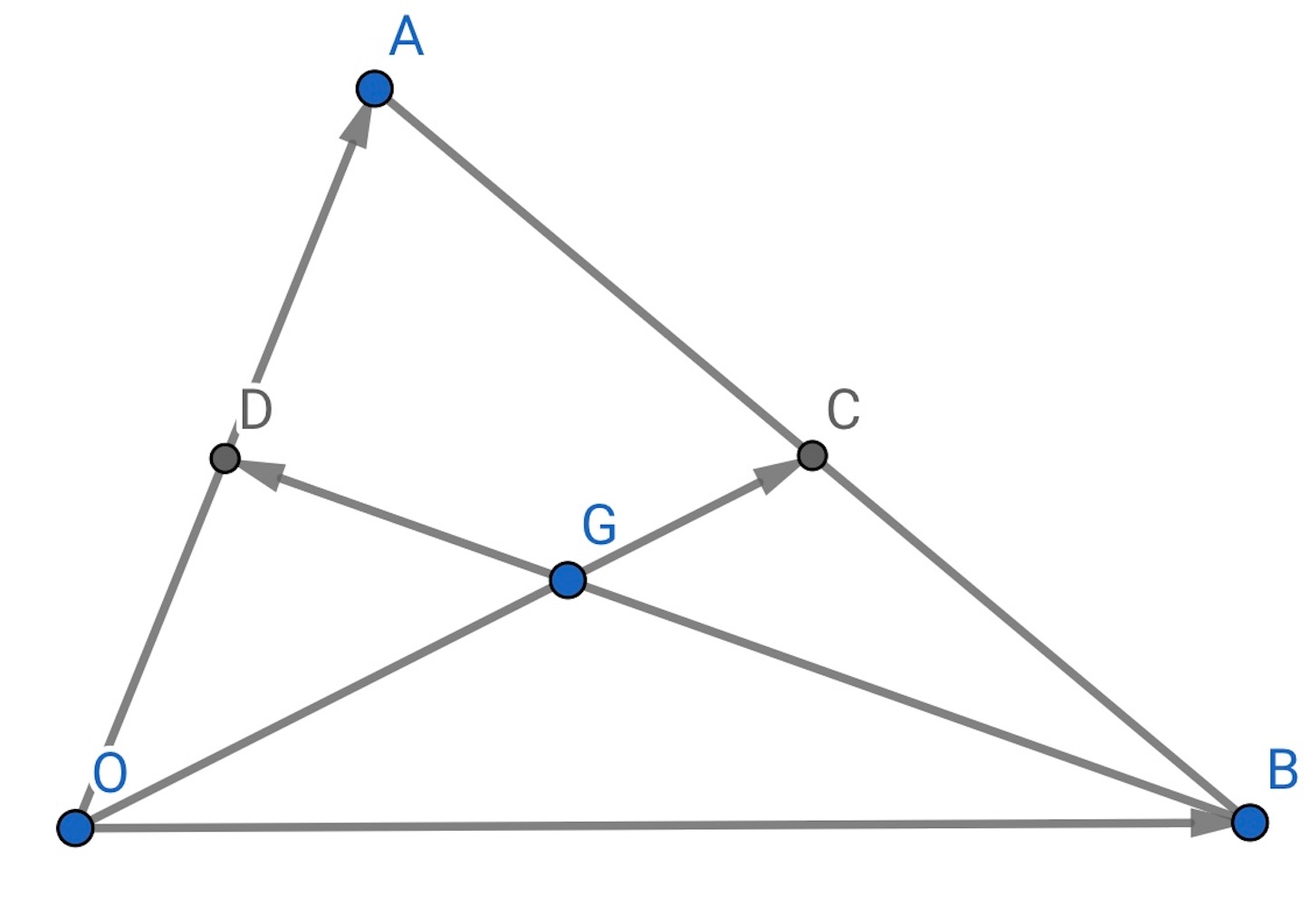
重心 の場合は,
,
を実数として,
したがって,
から,
となって,
というあたり前の結果が出て, ,
だから,
,
,
となって, 重心
は常に
の内部にあることが証明できた.
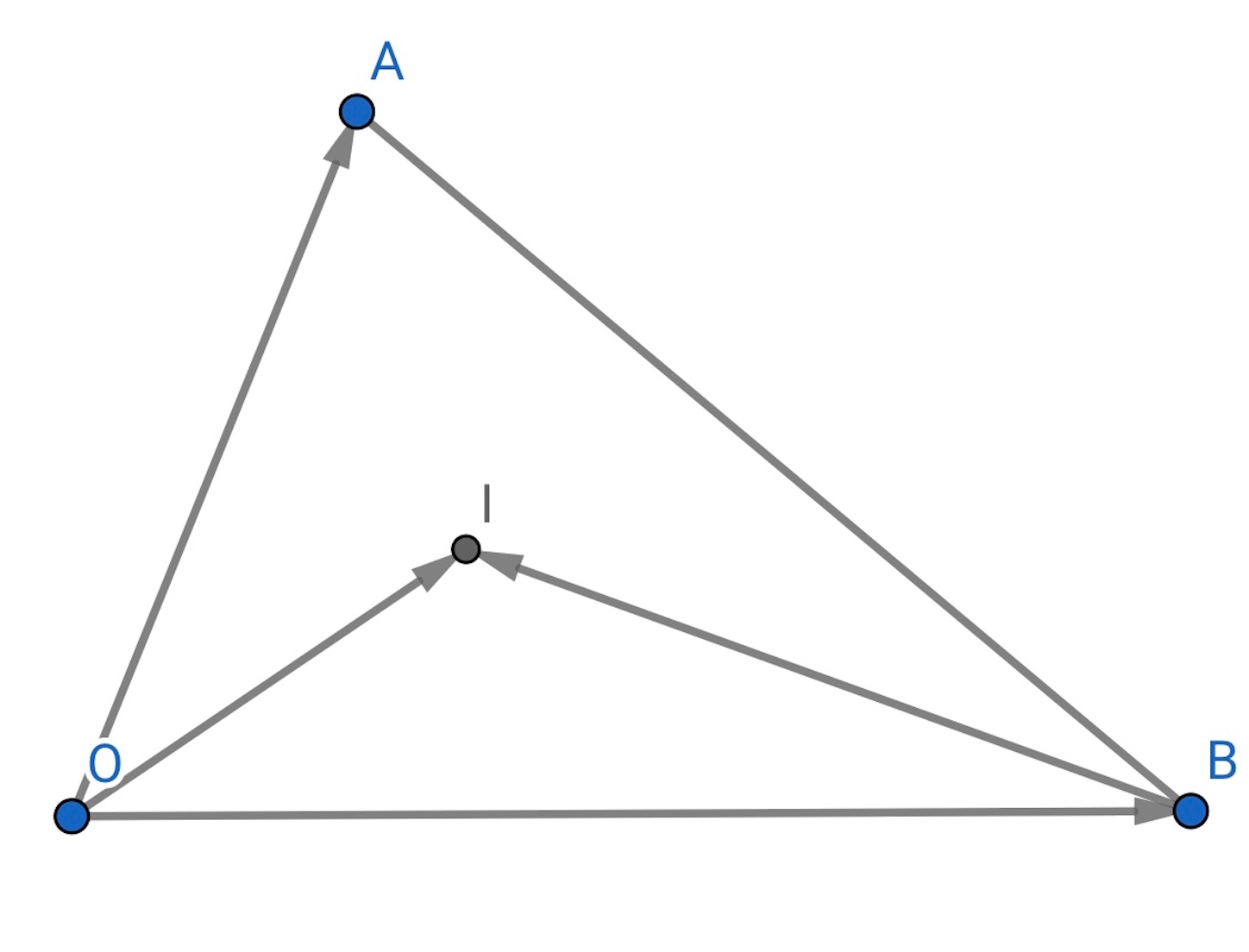
内心 の場合は,
,
,
とし, 角の
等分線を単位ベクトルで表わすことにして,
,
を実数とし,
したがって,
から,
となって,
という結果が出て,
,
だから, ,
,
となって, 内心
は常に
の内部にあることが証明できた.
なお, もし, 内心と重心が一致していたら,
から, なので, そのような三角形は, 正三角形しかないこともわかる.
(内心, 外心, 重心, 垂心のうち, どれか つが一致することがわかったら, その三角形は正三角形で, 前記の各心は全部一致することが証明できる.)
//
※ ベクトルの始点 を任意にとる場合, 点
が任意の
の内部にあるための必要十分十分条件は,
,
なる実数
,
,
があることである.
//
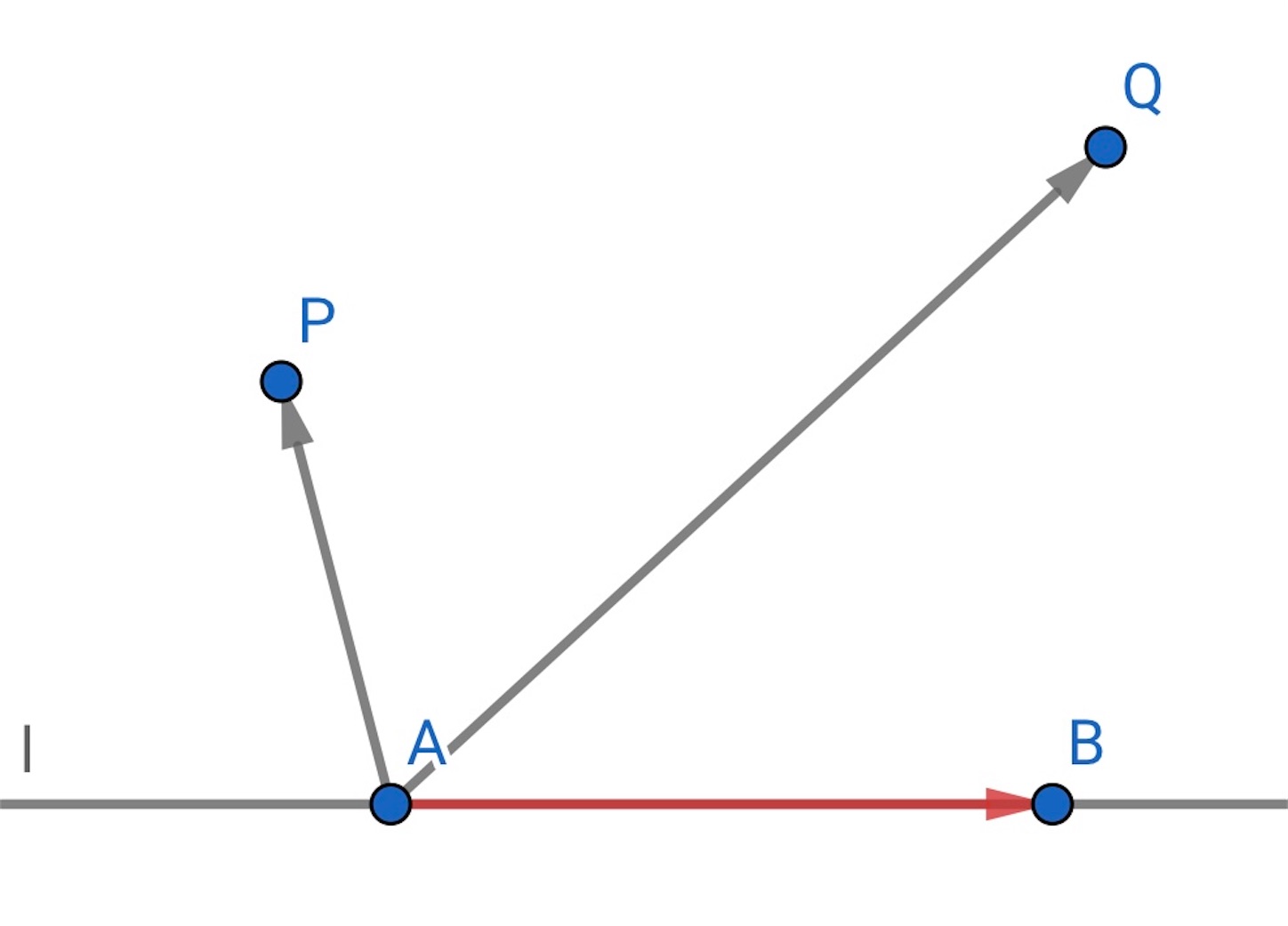
※ 「同じ側」をベクトルでいえば, 次のように定義することもできる.
直線 上にはない
点
,
と,
上の
点
,
に対して,
なる実数 ,
が存在するとき,
は
と
に関して同じ側にあるという.
//