陥没地帯 (305) - ノリの悪い日記

記事 $(266)$ の結果から, 角の $2$ 等分線の長さを実際に求めることができる.

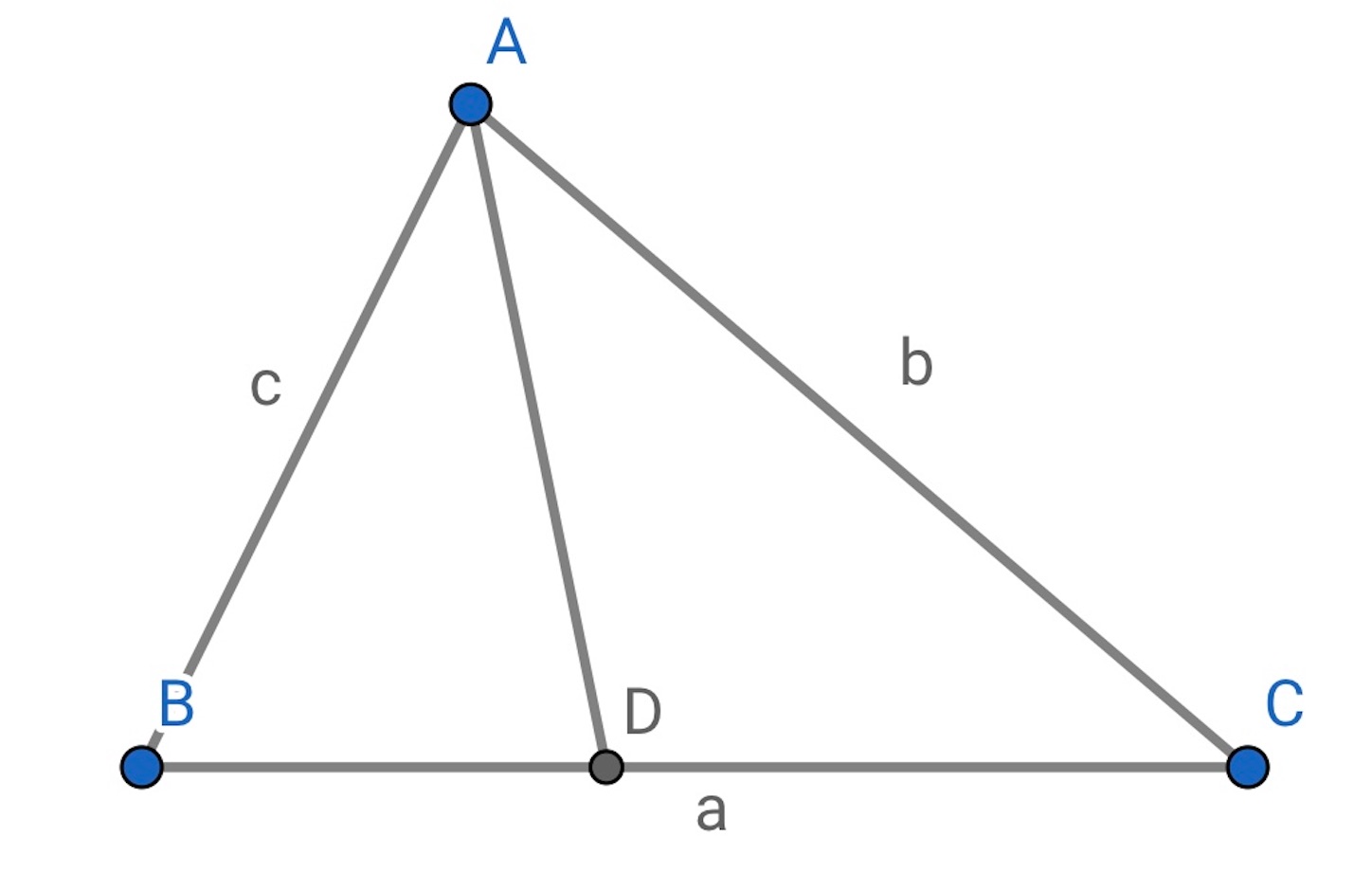
f:id:noriharu-katakura:20211213221507j:plain

$\begin{align} AD^2 &=bc - BD \cdot DC \\ BD &= \frac{ca}{b+c}\\ DC &= \frac{ab}{b+c}\\ \end{align}$

だから,

$\begin{eqnarray} AD^2 &=& bc-\frac{a^2bc}{(b+c)^2} \\&=& \frac{bc\{(b+c)^2-a^2\}}{(b+c)^2} \\&=& \frac{bc(a+b+c)(b+c-a)}{(b+c)^2} \\&=& \frac{4bcs(s-a)}{(b+c)^2} \end{eqnarray}$
//

「シュタイナー=レームスの定理」という下のような定理があるが, 上で求めた中線の長さを使って味もそっけもなく証明してみる.

【定理】
$\triangle ABC$ の $\angle B$ , $\angle C$ の $2$ 等分線と $AC$ , $AB$ の交点をそれぞれ, $D$ , $E$ とする. $BD = CE$ ならば, $AB= AC$ である.

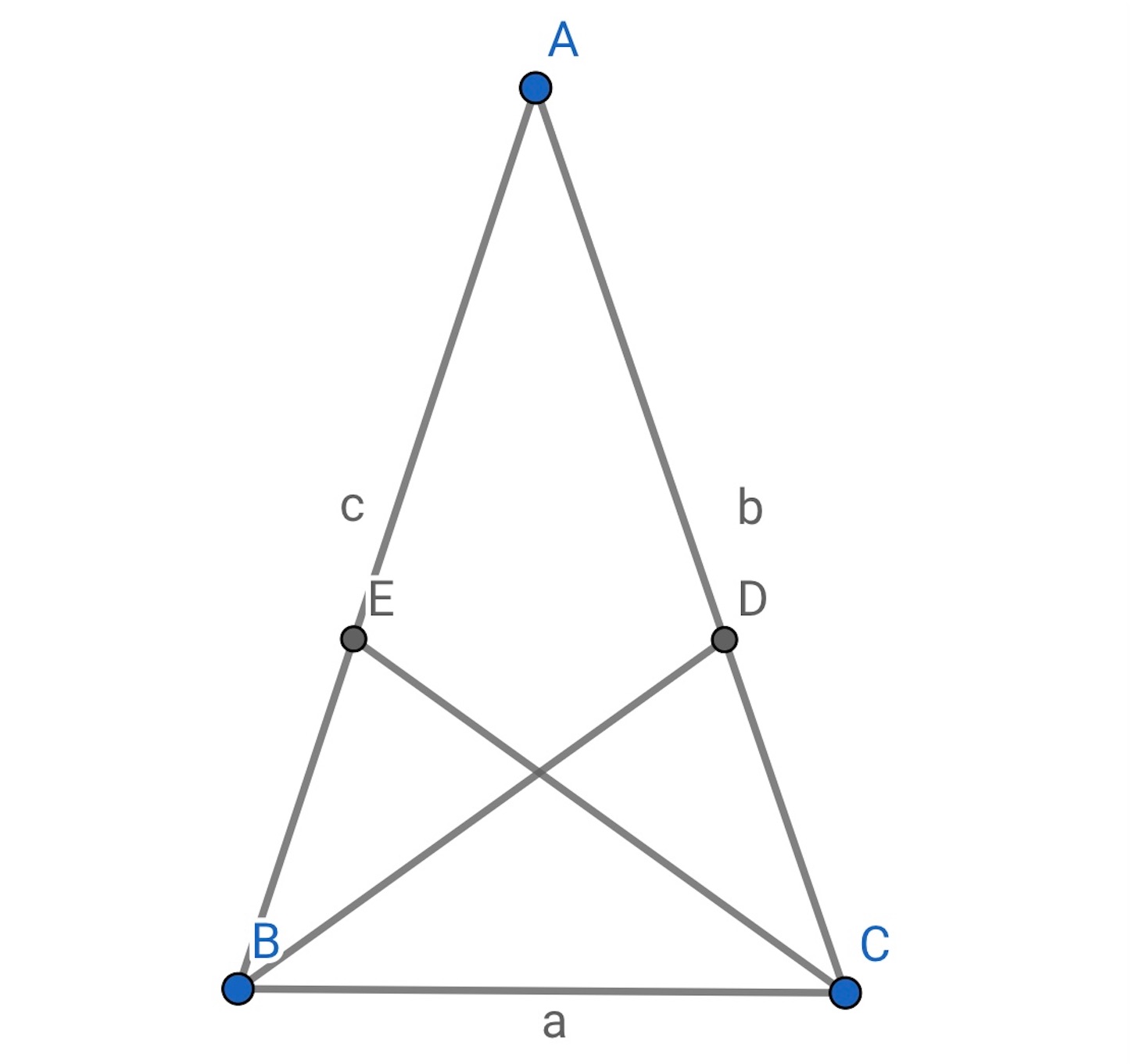
f:id:noriharu-katakura:20211213223909j:plain

【証明】
$AB = c$ , $BC = a$ , $CA= b$

とし,

$2s = a + b + c$

とする.

$\begin{align} BD^2 &=\frac{4acs(s-b)}{(a+c)^2}\\ CE^2 &=\frac{4abs(s-c)}{(a+b)^2}\\BD^2 &= CE^2 \end{align}$

から,

$\displaystyle{ \frac{c(s-b)}{(a+c)^2} = \frac{b(s-c)}{(a+b)^2} }$

これから,

$c(s-b)(a+b)^2 = b(s-c)(a+c)^2$

$\{b(a+c)^2 -c(a+b)^2\}s \\=bc\{(a+c)^2 - (a+b)^2\} \\= bc(2a+ b + c)(c-b) \\= bc(2s + a)(c-b)$

$b(a+ c)^2 - c(a+b)^2 \\= a^2b + bc^2 - ca^2 - cb^2 \\= (b-c)(a^2-bc)$

だから,

$(c-b)\{bc(2s+a)+(a^2-bc)s\} \\= (c-b)\{(a^2+bc)s+abc\} \\=0$

ここで,

$(a^2+bc)s+abc \neq 0$

から,

$b = c$

である.
//

f:id:noriharu-katakura:20211214024127j:plain

さらに, $BI$ の長さを求めよといわれたら, $\triangle BCE$ で, 記事の最初と同じ計算をしてもよいのだが, 内接円の半径を $r$ として,

$\begin{eqnarray} \frac{BI}{BD} &=& \frac{\triangle ABI + \triangle CBI }{\triangle ABC} \\&=& \frac{(a+c)r}{2sr} \\&=& \frac{a+c}{2s} \end{eqnarray}$