陥没地帯 (293) - ノリの悪い日記

$2021$ 年, 京都大学の問題.

【問】
f:id:noriharu-katakura:20211128192911j:plain

【解】
$(1)$
図を描いてみれば, すぐにわかるように, 外心は $(0,0)$ で, 外接円の半径は, $2$ である ( $A$ が $(0, 2)$ にあるときは正三角形である).

$(2)$
点 $A$ の座標を

$(2\cos \theta, 2\sin \theta)$
$0 < \theta < \pi$

とおく. また, 垂心 $H$ の座標を $(X, Y)$ とおく.

$H$ は, $A$ から, $BC$ へ下ろした垂線上にあるから,

$X = 2\cos \theta$

$\displaystyle{\theta = \frac{\pi}{6}}$ のとき, 垂心は点 $C$ なので, $Y = -1$ .

$\displaystyle{\theta \neq \frac{\pi}{6}}$ とすると, $AC$ の傾きは,

$\displaystyle{\frac{2\sin \theta + 1}{2\cos \theta - \sqrt{3}}}$

だから, $B$ から $AC$ に下ろした垂線の傾きは,

$\displaystyle{\frac{\sqrt{3} - 2\cos \theta} {2\sin \theta + 1}}$

となる. したがって,

$\displaystyle{Y = \frac{\sqrt{3} - 2\cos \theta} {2\sin \theta + 1}(X+ \sqrt{3}) -1}$

この式に, $X = 2\cos \theta$ を代入して,

$\begin{eqnarray} Y &=& \frac{\sqrt{3} - 2\cos \theta} {2\sin \theta + 1}(2\cos \theta+ \sqrt{3}) -1 \\&=& \frac{-4\cos^2 \theta+3} {2\sin \theta + 1} -1 \\&=& \frac{4\sin^2 \theta-1} {2\sin \theta + 1} -1 \\&=& 2\sin\theta-2 \end{eqnarray}$

したがって, $(X, Y) = (2\cos \theta, 2\sin \theta -2)$ となる ( $\displaystyle{\theta = \frac{\pi}{6}}$ のときもみたす).

$0 < \theta < \pi$ から, $-1 < \cos \theta < 1$ , $0 < \sin \theta \leq 1$ なので, 垂心 $H$ は,

$-2 < X < 2$ , $-2 < Y \leq 0$ で,

$X^2 + (Y+2)^2 = 4$ の円周上を動く.

f:id:noriharu-katakura:20211128221801j:plain
//

※ 以上のように解いたが, 実は記事 $(211)$ のオイラー線を知っていれば, この問題はほとんど計算しなくてよいのである. 問 $(1)$ で外心の座標を求めさせているのは, オイラー線への誘導と考えられるだろう.

三角形 $ABC$ の重心 $G$ の座標は, すぐに求めることができ,

$\displaystyle{\left(\frac{2\cos \theta}{3}, \frac{2\sin \theta -2}{3}\right)}$

となるが, オイラー線は,

$\overrightarrow{OH} = 3 \overrightarrow{OG}$

ということに他ならないから,

$\displaystyle{\overrightarrow{OH} = (2\cos \theta, 2\sin \theta -2) }$

である. なお, $\triangle ABC$ が正三角形のときは, もちろん, 外心, 垂心, 重心は一致する.
//

※ 念のため, 記事 $(211)$ のオイラー線の部分を再掲しておく.

正三角形を除く三角形の外心 $O$ , 重心 $G$ , 垂心 $H$ はオイラー線と呼ばれる同一直線上にあり, $G$ は線分 $OH$ を $1:2$ の比に内分する.

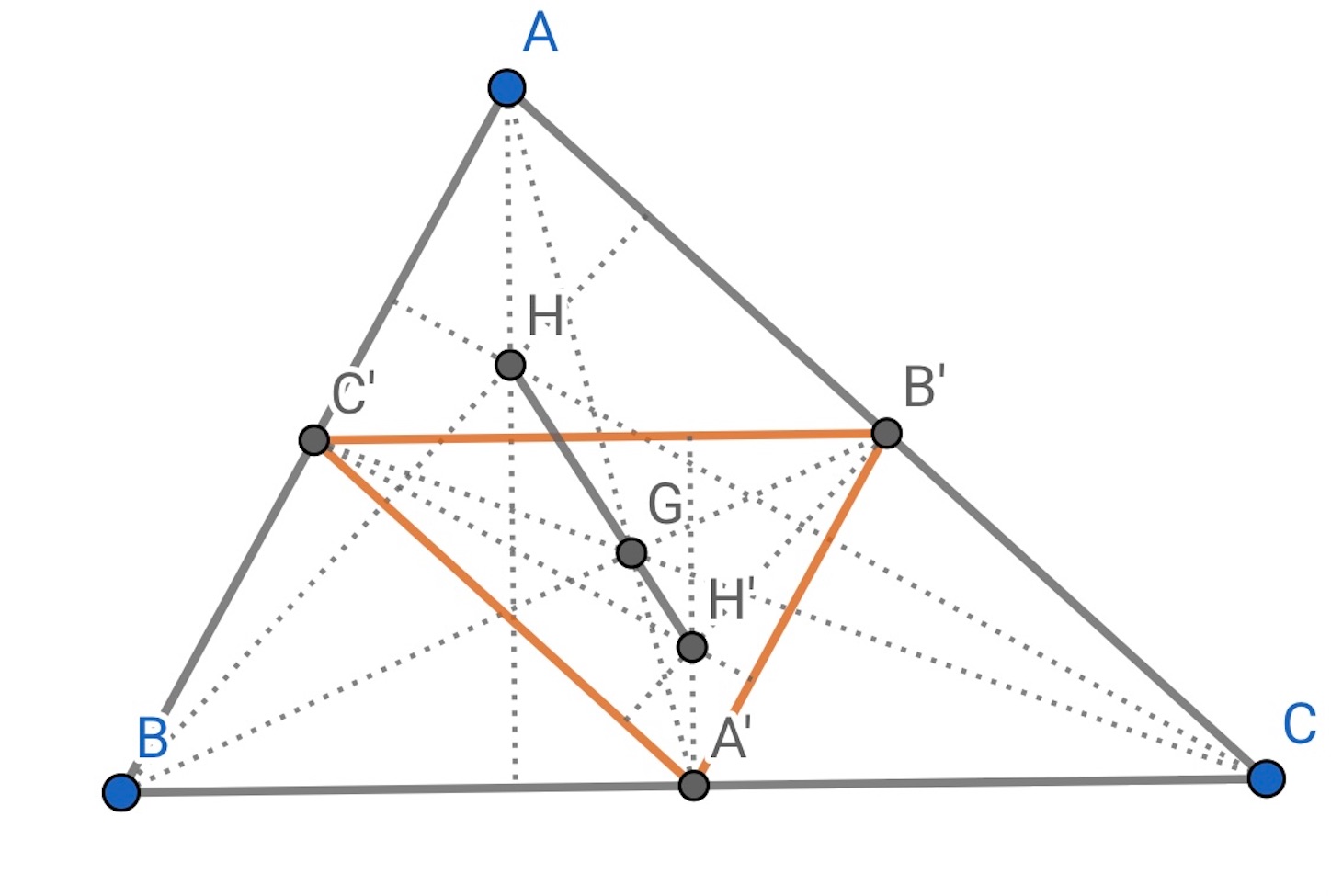
f:id:noriharu-katakura:20210712121224j:plain

$A'$ , $B'$ , $C'$ は $\triangle ABC$ の重心 $G$ を中心とし, $A$ , $B$ , $C$ をそれぞれ相似比 $-1/2$ で中心相似変換したものだから, $\triangle ABC$ と $\triangle A'B'C'$ は相似の位置にある (したがって $\triangle ABC$ と $\triangle A'B'C'$ は相似である). ところが, $\triangle A'B'C'$ の垂心 $H'$ は, $\triangle ABC$ の外心 $O$ と一致する. よって題意が成立する.//