年, 東大理科の問題. 問題を解くより,
でどうやって遷移図を描くのか調べる方がはるかに時間がかかった.
【問】

【解】
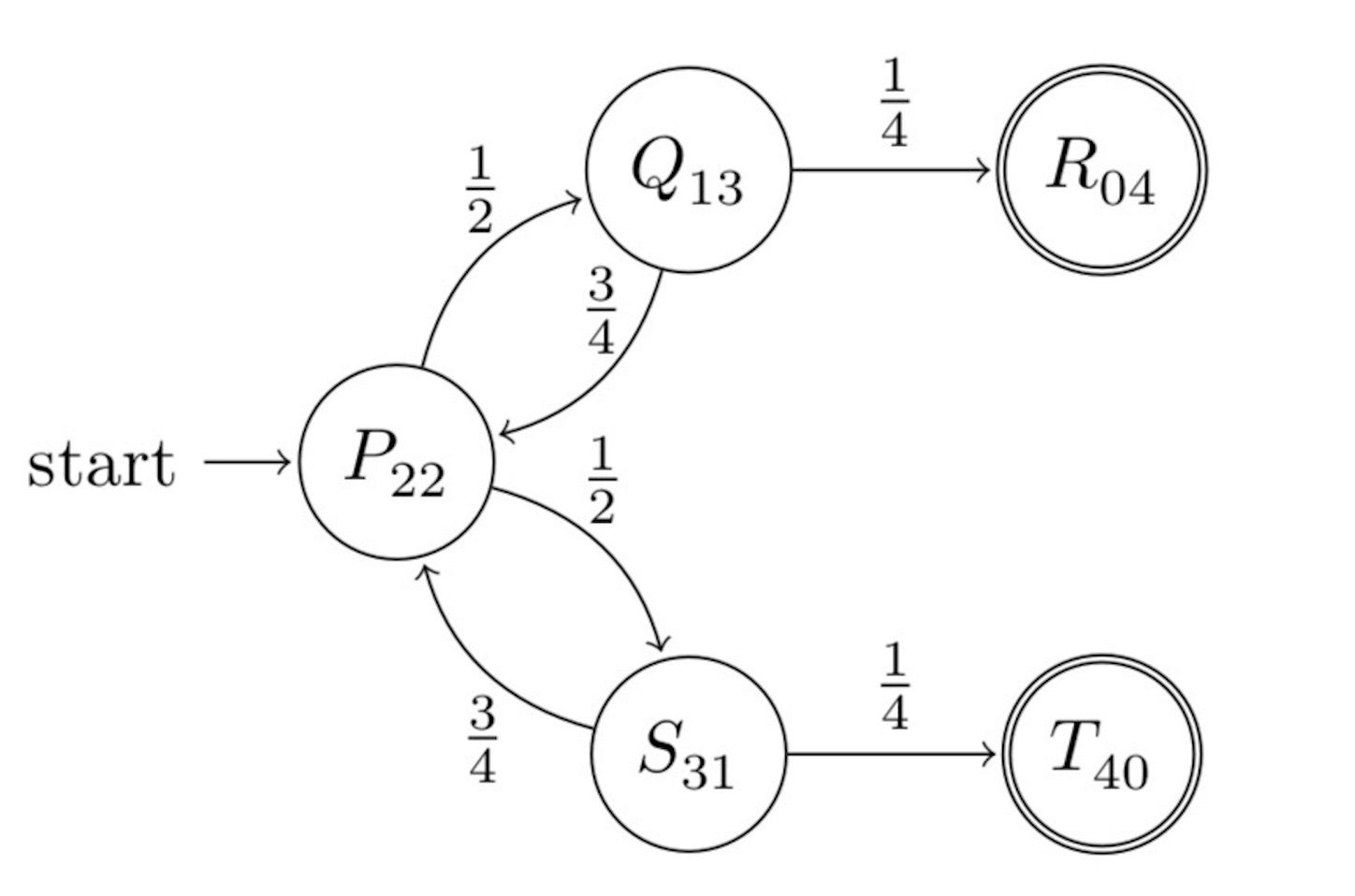
明らかに が偶数の場合しか終状態に到達しえないので,
を偶数とし,
回目で, 終状態
または
に到達する確率を
とする. また,
回目で状態
にいる確率を
とする. すると, 遷移の対称性から,
ところで,
で であるから,
となる*1. したがって, が偶数のとき,
で, が奇数のとき,
である.
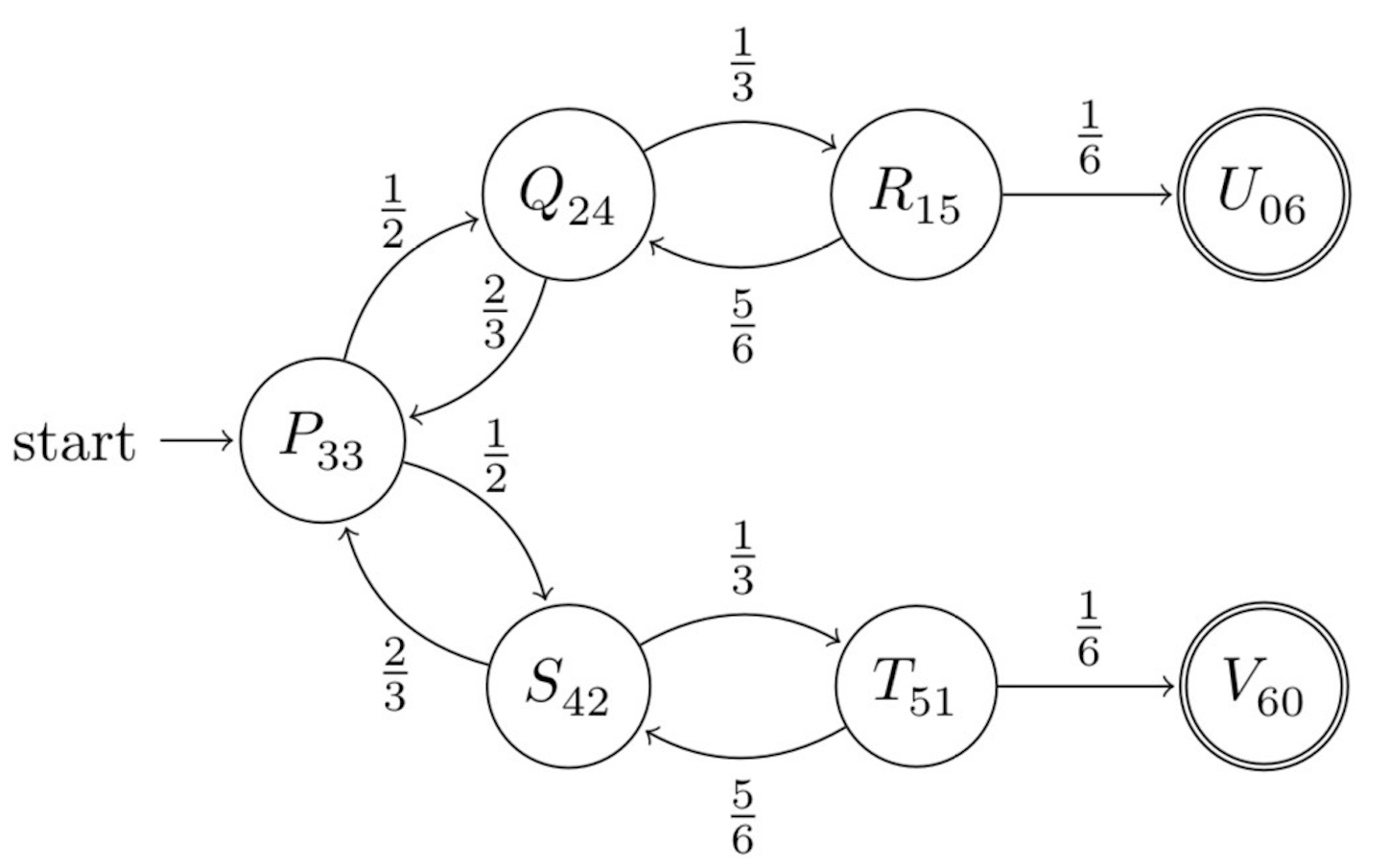
明らかに が奇数の場合しか終状態に到達しえないので,
を奇数とし,
回目で, 終状態
または
に到達する確率を
とする. また,
回目で状態
にいる確率を
とする (状態
にいる確率も遷移の対称性から, 同じ
である). すると,
ところで,
で, であるから,
となる. したがって, が奇数 (ただし,
) のとき,
で, が偶数 および
のとき,
である.
//
*1:指数の は,
と書いてみて, 仕切り線 ‘
’ が何個あるかを植木算で数え上げれば, その個数が公比を何回かけるのかに対応しているので求めることができる. 問
の奇数のときも同様である.