陥没地帯 (267) - ノリの悪い日記

数え上げの問題で「全単射による証明」を目にするたびに, 「賛嘆措く能わず」という気分になるのだが, この証明について, 初等的にきちんと解説したものはあまり見受けられないのではないかと思う. 英語版の Wikipedia の “bijective proof” の項はよくまとまっている方だと思うので, 少し訳してみることにする. 二項係数で,

${}_{n}\mathrm{C}_{k} = {}_{n}\mathrm{C}_{n-k}$

であることを例にとって, 組合せ論的な証明を説明している条 (くだり) である.

証明の基本アイデアは, 次の簡単な例から理解できるかもしれない. $n$ 人の子供のグループから, ご褒美にアイスクリームコーンが与えられる $k$ 人を選抜する代わりに, アイスクリームコーンを貰えない $n -k$ 人の子供を選ぶことはまったく同じ効果をもつ.
より抽象化, 一般化すると, 等しいと主張される $2$ つの数量は, $n$ 個の要素をもつ任意の集合 $S$ の $k$ 個, $n-k$ 個の要素をもつ部分集合をそれぞれ数えている. $A$ を $S$ の $k$ 個の要素をもつ部分集合の集合とすると, 集合 $A$ は, ${}_n\mathrm{C}_k$ 個の要素をもつ. $B$ を $S$ の $n-k$ 個の要素をもつ部分集合の集合とすると, 集合 $B$ は, ${}_n\mathrm{C}_{n-k}$ 個の要素をもつ. $2$ つの集合 $A$ , $B$ の間には次のような単純な全単射写像が存在している. その写像は, 任意の $k$ 個の要素をもつ部分集合 (集合 $A$ の要素である) をその補集合, つまり, $S$ の残っている $n -k$ 個の要素を正確に含み, したがって $B$ の要素である集合に対応させる. もっと形式化すれば, このことは, 写像表記を使って次のように書ける. $f: A \rightarrow B$ は, $f(X) = X^{c}$ で定義され, ここで, $X$ は $k$ 個の要素をもつ集合 $S$ の任意の部分集合で, 補集合は $S$ においてとられるものとする. $f$ が全単射であることを示すために, 最初に $f(X_1) = f(X_2)$ , つまり $X_1^c = X_2^c$ であると仮定する. 両辺の補集合を ( $S$ において) とると, 集合の補集合の補集合は, もとの集合であるという事実を用いて, $X_1 = X_2$ であることを得る. これは, $f$ が単射であることを示す. 次に, $n-k$ 個の要素をもつ集合 $S$ の任意の部分集合を $B$ からひとつ取り, これを $Y$ とする. その $S$ における補集合である, $Y^c$ は, $k$ 個の要素をもつ部分集合であり, したがって $A$ の要素である. $f(Y^c) =(Y^c)^c=Y$ であるので, $f$ は全射でもあり, かくして $f$ は全単射である. 有限集合の間に全単射が存在することは, 両者の要素数が同じである, すなわち, ${}_{n}\mathrm{C}_{k} = {}_{n}\mathrm{C}_{n-k}$ ということを示すので, 結果が従う.

この場合, 全単射であることの証明には, 可逆な一組の写像が存在することを示す方が簡単な気もする. すなわち,

$2$ つの写像 $f: A \rightarrow B$ と $g: B \rightarrow A$ が $g \circ f=i_A$ , $f \circ g=i_B$ を満たせば, $f$ , $g$ ともに全単射であって, $f^{-1} = g$ , $g^{-1} = f$ が成り立つ. (ここで, $i_A$ , $i_B$ はそれぞれ, 集合 $A$ , $B$ の自分自身への恒等写像を表わす.)

という定理があるので, この場合, $A$ の要素の補集合を取る操作を写像 $f$ とし, $B$ の集合の補集合を取る操作を写像 $g$ とすれば, 上の定理における可逆操作成立の条件を満たすので, $f$ は全単射である.

ついでに言っておけば, $f$ が単射ならば, 有限集合*1 $B$ の要素の個数は, 有限集合 $A$ の要素の個数以上あるという命題が成り立つが, この命題の対偶が「鳩の巣原理」とか「部屋割り論法」とか特別な名称で言われているものである.

有限集合の場合には, いろいろな話が簡単になる. (空でない) 有限集合 $A$ , $B$ の要素の個数が等しいとき, $f: A \rightarrow B$ が単射であるならば全射でもある (つまり全単射である) ことが以下のようにしていえる. $f$ は単射だから, $a_1, a_2 \in A$ が, $a_1 \neq a_2$ であれば, $f(a_1) \neq f(a_2)$ である. そうすると, $f$ の像 $f(A)$ の要素の個数と $A$ の個数の要素は等しく, $A$ の要素の個数と $B$ の要素の個数は等しいのだから, $f$ は全射でもある (全単射である). 同じようにして, (空でない) 有限集合 $A$ , $B$ の要素の個数が等しいとき, $f: A \rightarrow B$ が全射であるならば単射でもある (つまり全単射である) ことが以下のようにしていえる. $f$ は全射であるから, 任意の $b \in B$ に対して, $f(a) = b$ となる $a \in A$ が存在する. すると, $f(a_1) = f(a_2)$ で $a_1 \neq a_2$ が存在するとすると, $A$ の要素の個数が $B$ の要素の個数よりも多いことになって矛盾する. したがって, $f$ は単射でもある (全単射である).

有限集合 $A$ , $B$ があって, $f: A \rightarrow B$ , $g: B \rightarrow A$ がともに単射であるとすると, 有限集合 $A$ と有限集合 $B$ の個数は等しいことがわかるので, $f$ , $g$ はともに全単射となる.
※ 上の命題は, 単射を全射にしても成立する.
※ 集合が無限集合の場合には, ベルンシュテインの定理というのがあって, 単射である $f: A \rightarrow B$ , $g: B \rightarrow A$ が存在すると全単射写像が存在し, 集合 $A$ と集合 $B$ の濃度は対等になるということが証明されている. ただし, 単射である $f$ , $g$ が全単射になるとは限らない.//

整数の分割やカタラン数の数え上げなどに, よくこの「全単射による数え上げ」が出てくる. 以下は整数の分割*2の例である.

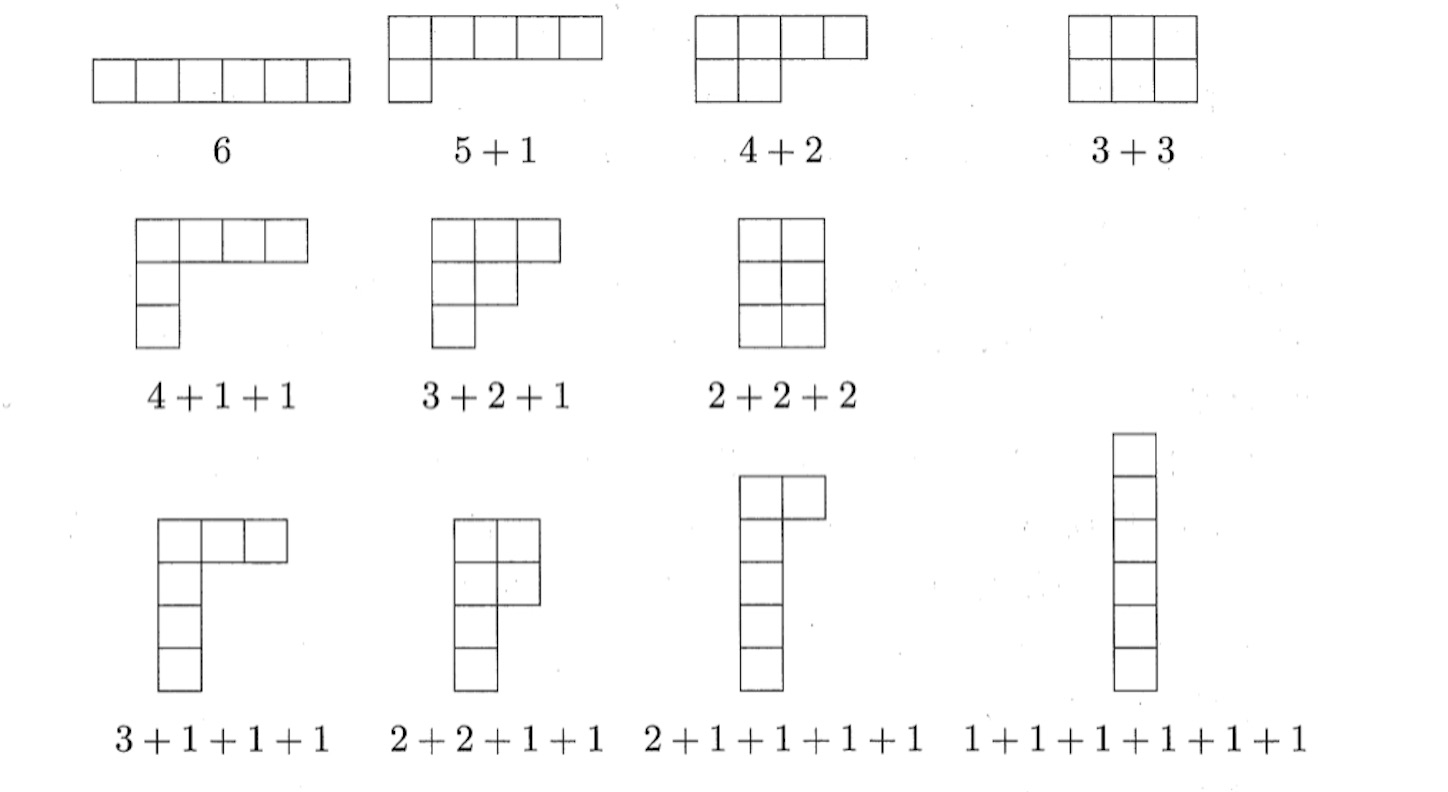
f:id:noriharu-katakura:20211030122243j:plain

上のヤング図形が示す通り $6$ の分割の仕方は, $11$ 通りあるが, $6$ を $3$ 以下の自然数の和で表わすやり方を数えてみると $7$ 通りである. 一方, $6$ を $3$ 個以下の自然数の和で表わすやり方を数えてみると, やはり $7$ 通りである. これは偶然の一致ではない. このことは, 上の Wikipedia の説明にならって, 部分集合 ( $3$ 個以下の自然数の和の集合と $3$ 以下の自然数の和の集合) をそれぞれつくり, その部分集合の間に全単射写像が存在すること (要するに全部漏れもなく, 重なりもなくペアにできる操作が存在すること) を示せばよい. この場合の全単射写像とは, ヤング図形の行と列を入れ替える操作 (あるいは左上の頂点を原点とし, $y = -x$ を対称軸として図形を折り返す鏡映操作) である！

$6 \leftrightarrow 1+1+1+1+1+1\\ 5+1 \leftrightarrow 2+1+1+1+1\\ 4+2 \leftrightarrow 2+2+1+1\\ 3+3 \leftrightarrow 2+2+2\\ 4+1+1 \leftrightarrow 3+1+1+1\\ 3+2+1 \leftrightarrow 3 + 2 +1\\ 2+2+2 \leftrightarrow 3+3$

*1:自然数の部分集合との間に全単射写像が存在し, その対応する自然数の部分集合に最大数があるものをいう. 自然数の部分集合との間に全単射写像が存在し, その対応する自然数の部分集合に最大数がなければ「可算」という. 「可算」は無限の一種である. なお可算集合に有限集合を含める流儀もあるのではっきりさせたい場合には「可算無限」集合という.

*2:正の整数 $N$ を正の整数の有限個の列 $a_1 \geq a_2 \geq \cdots \geq a_n$ を用いて, $N = a_1+ a_2 + \cdots + a_n$ と表わすことを言う．このときの $a_i$ を和因子という．