陥没地帯 (254) - ノリの悪い日記

難問揃いで知られる $1990$ 年の東大理科の問題のひとつ. 眠いし, かなり難易度高いので, まず問 $(1)$ だけやった. $(1)$ も普通に解こうとするとすごいことになりそうなので, 記事 $(248)$ の平均変化率の方法を活用して解くことを考えた.

※ 問 $(2)$ もその後, 解いたので, この記事に追記する. 対称性を利用することをなかなか思いつかなかった.

【問】

f:id:noriharu-katakura:20211015040558j:plain

【解】
$(1)$
まず, $(\mathrm{i})$ の条件を使って,

$h(x) = (x-1)(x+1)(px+q) +x$

とおく. 微分すると,

$h'(x) = (x+1)(px+q)+(x-1)(px+q) \\ \quad + p(x+1)(x-1) + 1$

$x = \alpha$ で極大, $x= \beta$ で極小をとるとすると,

$h(\alpha) = 1$ , $h(\beta) = -1$ から,

$(\alpha +1)(p\alpha +q) +1 = 0 \quad (\mathrm{A})$
$(\beta-1)(p\beta +q) +1 = 0 \quad (\mathrm{B})$

$h'(\alpha) = 0$ , $h'(\beta) = 0$ と上の式を使って,

$p\alpha +q+p(\alpha+1) = 0$
$p\beta +q+p(\beta -1) = 0$

となり, 両式の各辺をそれぞれ足して, $p \neq 0$ より,

$\displaystyle{ \alpha + \beta = - \frac{q}{p}}$

また, 両式の各辺をそれぞれ引いて,

$\alpha - \beta = - 1$

となる.

$(\mathrm{A})-(\mathrm{B})$ から,

$p\{(\alpha + \beta)(\alpha-\beta) + \alpha + \beta\} \\ \quad+ q(\alpha-\beta) =0$

なので, $q = 0$ となり, これから, $\alpha = -1/2$ , $\beta = 1/2$ で, $(A)$ 式から, $p = 4$ となる. 以上より,

$h(x) = 4x^3 -3x$

$(2)$
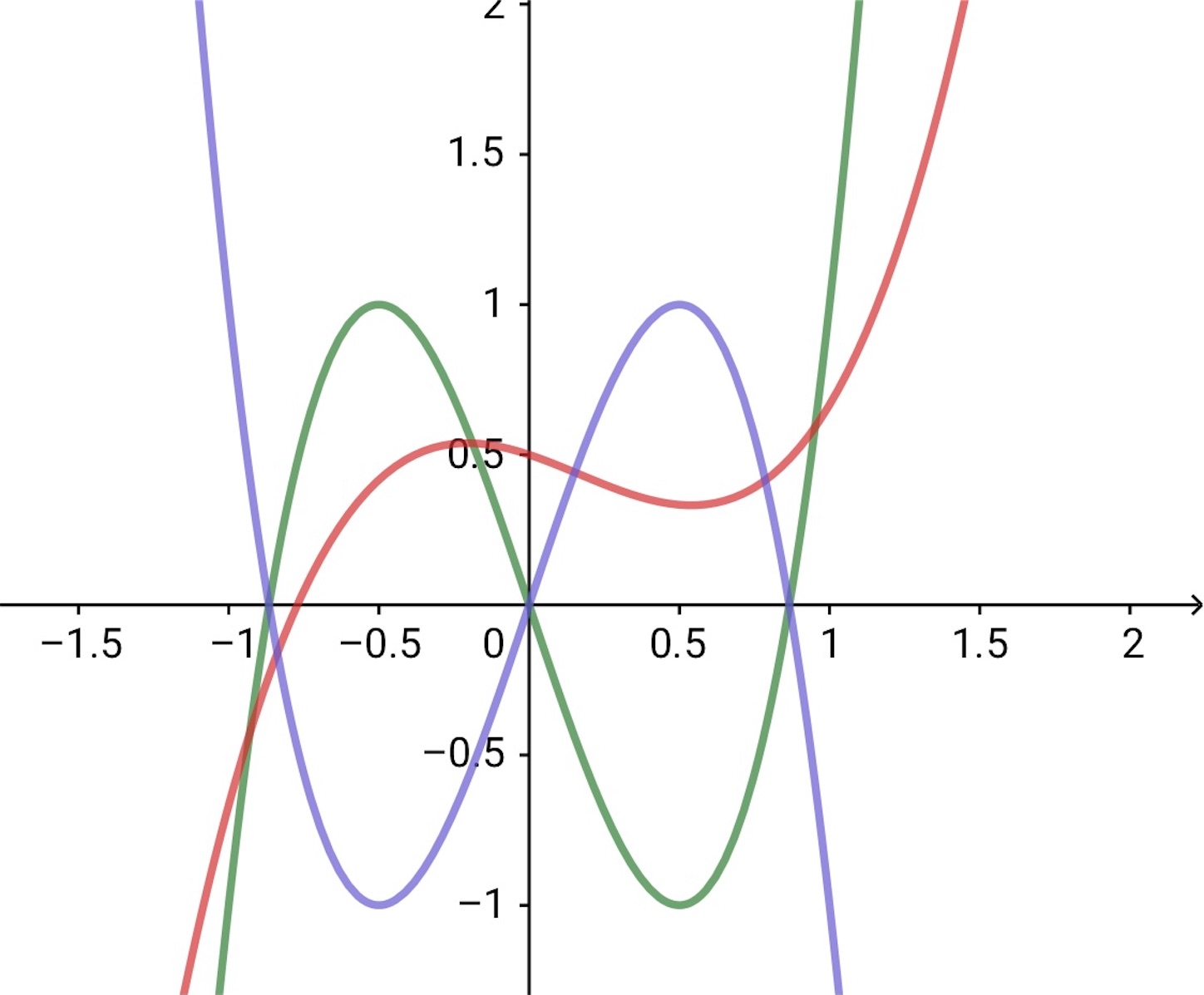
f:id:noriharu-katakura:20211015161100j:plain

$h(x)$ は $h(-1) = -1$ , $h(-1/2) = 1$ , $h(1/2) = -1$ , $h(1) = 1$ をとる連続な関数だから, 問の条件を満たす $f(x)$ は, $-1 \leq x < -1/2$ , $-1/2 < x < 1/2$ , $1/2 < x \leq 1$ でそれぞれ少なくとも $1$ 回, $h(x)$ と交るが, 交点の総数は $3$ を超えることはないから, 結局, $|x| \leq 1$ で, $f(x)$ は, $h(x)$ とちょうど $3$ 回交わる. したがって, $|x| > 1$ で, $f(x)$ は, $h(x)$ と交点を持つことはない.

まったく, 同様の議論を, 今度は $-h(x)$ について考察すると, $|x| \leq 1$ で, $f(x)$ は, $-h(x)$ とちょうど $3$ 回交わる. したがって, $|x| > 1$ で, $f(x)$ は, $-h(x)$ と交点を持つことはない.

そうすると, $|x| > 1$ で $f(x)$ は, $-|h(x)| < f(x) < |h(x)|$ を常にみたす. つまり, $|f(x)| < |h(x)|$ をみたす.

※ ややこしく書くとこうなる.

中間値の定理を使うために, 実数全体で連続な $g(x) = h(x) - f(x)$ を定義すると, $g(-1/2) > 0$ , $g(1/2) < 0$ である. したがって, 中間値の定理から, $h(x)= 0$ となる $-1/2 < x < 1/2$ が少なくともひとつ存在する.

さらに, $g(-1) <0$ または $g(1) > 0$ であれば, 中間値の定理から, $g(x) = 0$ となる $x$ が, $-1 < x < -1/2$ , $1/2 < x < 1$ にそれぞれ少なくともひとつ存在する. また, $g(-1) = 0$ または $g(1) = 0$ であれば, その点が交点である. なお, $g(-1) > 0$ , $g(1) < 0$ は $f(x)$ が連続であることに矛盾する.

$3$ 次多項式の交点の総数は $3$ を超えることはないから, 結局, $|x| \leq 1$ で, $f(x)$ は, $h(x)$ とちょうど $3$ 回交わる.

上のことから, $x < -1$ で, $h(x)$ と $f(x)$ は交点をもたない. したがって, $g(x) = 0$ とならず, 中間値の定理 (の対偶) により, $g(-1) < 0$ ( $g(-1) = 0$ のときは, $g(-1 -0) < 0$ ) と異符号にもならないので,