陥没地帯 (248) - ノリの悪い日記

組立除法は要らないとか, 一応知っているだけという人がいるかもしれないので, あえて書くのだが, そういう人って, もしかしたら,

$f(x) = x^3+2x^2+3x+1$

とか与えられていて, $f(3)$ を求めるときに,

$f(3) = 3^3+2\times 3^2+3\times 3+1$

を計算して, $55$ と出しているのかもしれない. 組立除法を使えば,

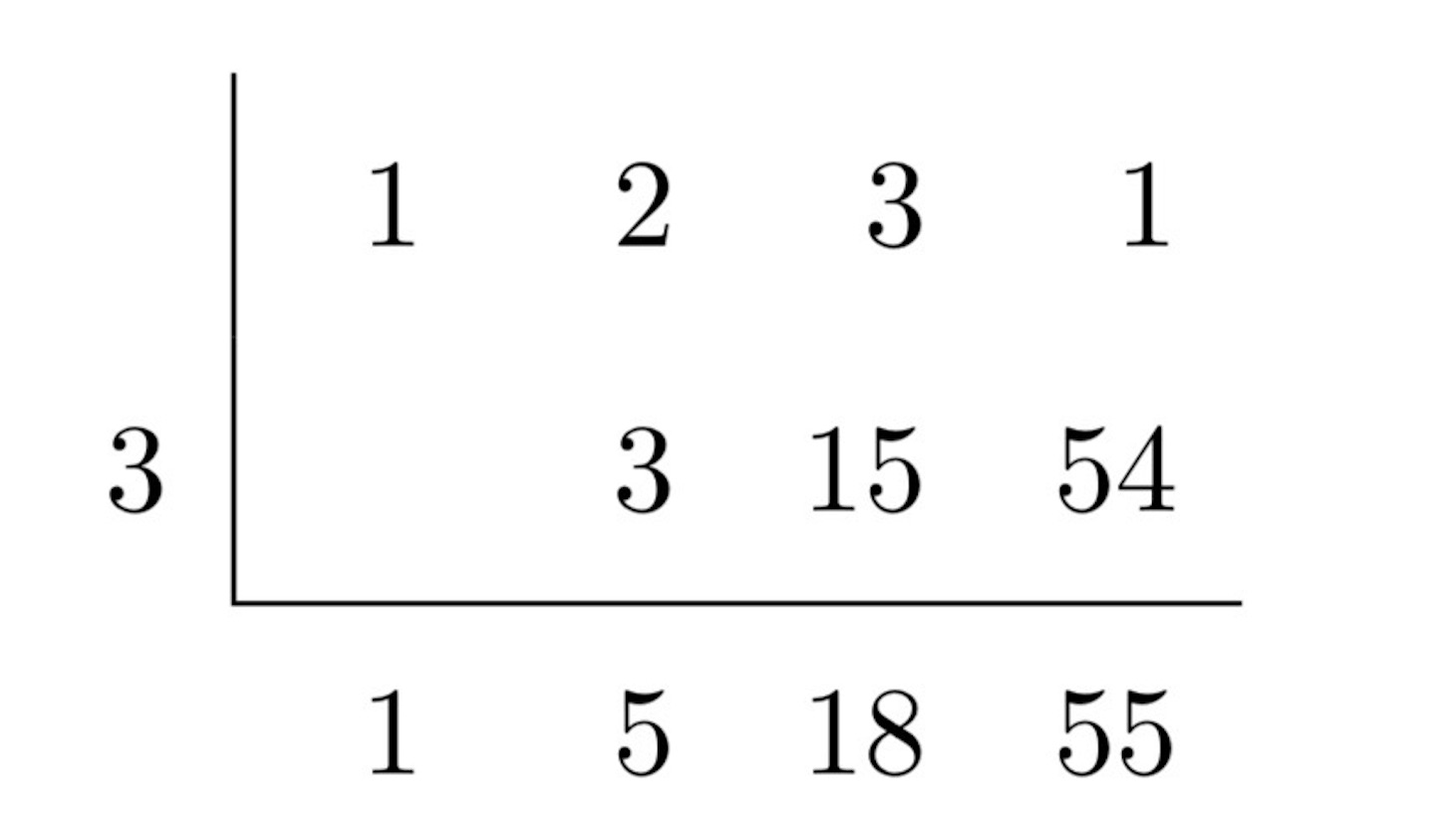
f:id:noriharu-katakura:20211009123739j:plain

となって, こちらの方が早い気がする. $2$ 進法を $10$ 進法に変換するのだって, たとえば, $2$ 進法で, $10110011$ ならば,

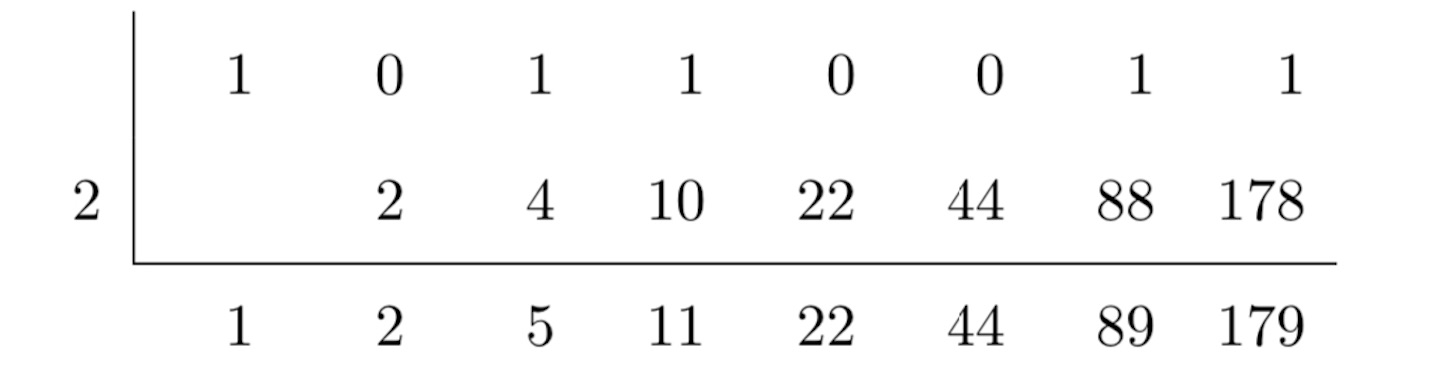
f:id:noriharu-katakura:20211009124657j:plain

と計算する方が早いのではないだろうか.

たとえば, $f(x) = 4x^3 -3x^2+2x-1$ の $x = 1$ での接線の方程式は, もちろん微分係数を計算して求めることができるが, $f(x)$ を組立除法を使って $x-1$ で $3$ 回続けて割って,

$f(x) \\= 4(x-1)^3+9(x-1)^2 \\ \quad +8(x-1)+2 \\=(x-1)^2 (4x+5)+8x-6$

とすれば, 接線の方程式は, $y = 8x-6$ で, 接線の $x=1$ 以外のもうひとつの交点は, $x = -5/4$ だとわかる.

組立除法は, 計算機科学でいう Horner 法と基本的に同じ手法であり, 最も少ない加算と乗算の演算回数で $n$ 次の多項式の評価を行うことができるアルゴリズムである. かけ算をたくさんやりたい人以外は, 使わない手はないと思う.

※ 整式 $f(x)$ を $x-a$ で割って, その商を $q(x)$ , 余りを $r$ とする. すなわち,

$f(x) = (x-a)q(x) + r$

さらに, $a \neq b$ として, 商 $q(x)$ を $x-b$ で割って, その商を $q'(x)$ , 余りを $m$ とする. このとき,

$\begin{eqnarray} f(x) &=& (x-a)q(x) + r \\&=& (x-a)\{(x-b)q'(x) + m\} + r \\&=& (x-a)(x-b)q'(x) \\ &&\quad + m(x-a) + r \end{eqnarray}$

となる. $f(a) = r$ , $f(b) = (b-a)m+r$ だから,

$f(b) = (b-a)m + f(a)$

つまり,

$\displaystyle{m = \frac{f(b)-f(a)}{b-a}}$

となるので, 整式 $f(x)$ を $x-a$ で割った商をさらに $x-b$ で割った余り $m$ は, $x$ が $a$ から $b$ まで動いたときの平均変化率を表わすのである.

【例 $1$ 】
$3$ 点 $A(-1,2)$ , $B(1,-4)$ , $C(3,6)$ を通る $2$ 次関数を求めよ.

【解】求める $2$ 次関数は,

$f(x) = \alpha(x+1)(x-1) + m(x+1)+2$

とおける. $m$ は, 点 $A$ , 点 $B$ の間の平均変化率で,

$\displaystyle{m = \frac{-4-2}{1+1} = -3}$

となり,

$f(x) = \alpha(x+1)(x-1) -3(x+1)+2$

これに $C$ の座標を代入し

$8\alpha-10 =6$

から,

$\alpha = 2$

を得る. 以上から,

$\begin{eqnarray} f(x) &=& 2(x+1)(x-1) -3(x+1)+2 \\ &=& 2x^2 -3x -3 \end{eqnarray}$
//

【例 $2$ 】
$\displaystyle{\int_{-1}^{3}(x^3-x^2+ x -1)dx \\= \left[\frac{x^4}{4}-\frac{x^3}{3} + \frac{x^2}{2} -x\right]_{-1}^{3} \\= \frac{1}{12} \left[3x^4-4x^3+ 6x^2-12x\right]_{-1}^{3} }$

まず, $x+1$ で割って (最初に $x-3$ で割っても構わないけれど……),
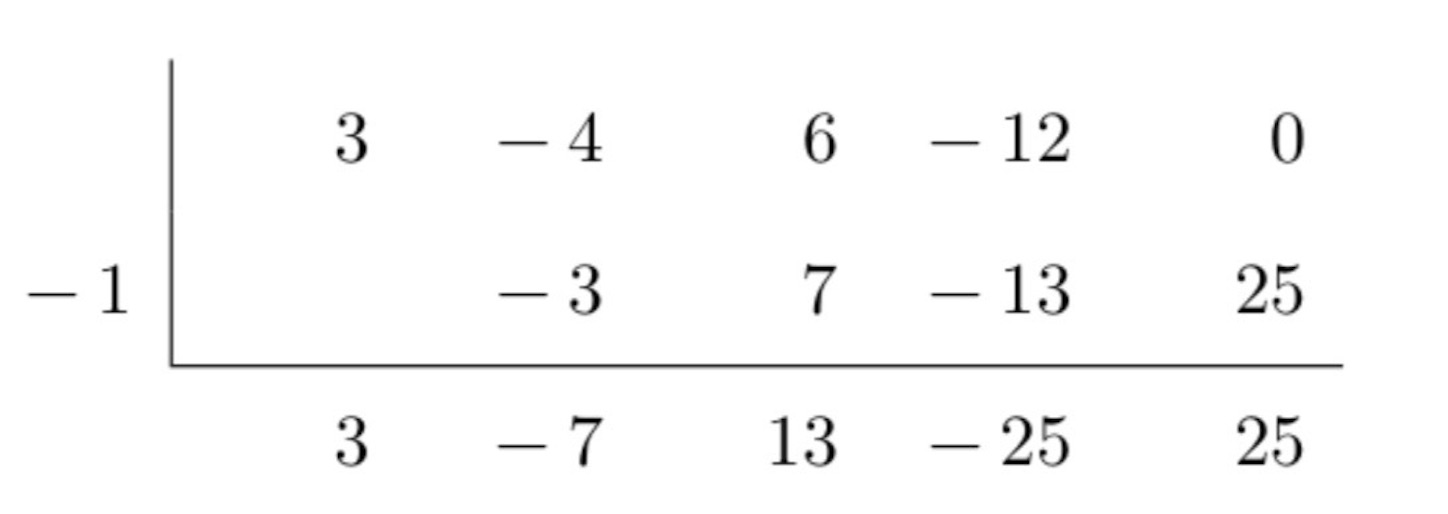
f:id:noriharu-katakura:20211009175027j:plain
さらに商を $x-3$ で割って余りを求める.

したがって, $m =32$ . 求める積分は,

$\displaystyle{\frac{32}{12}\{3-(-1)\}=\frac{32}{3}}$

である.//