簡単な問題だが, 昔から入試によく取り上げられる. 年, 京大の問題. なお, 与えられた
点を通り, 一本の直線に接する円の作図方法は, 記事
に示しておいた. 一般に円は
つ描ける.
【問】
を正の実数とする. 座標平面上の
点
,
,
をとり,
を考える.
の値が変化するとき,
の最大値を求めよ.
【解】
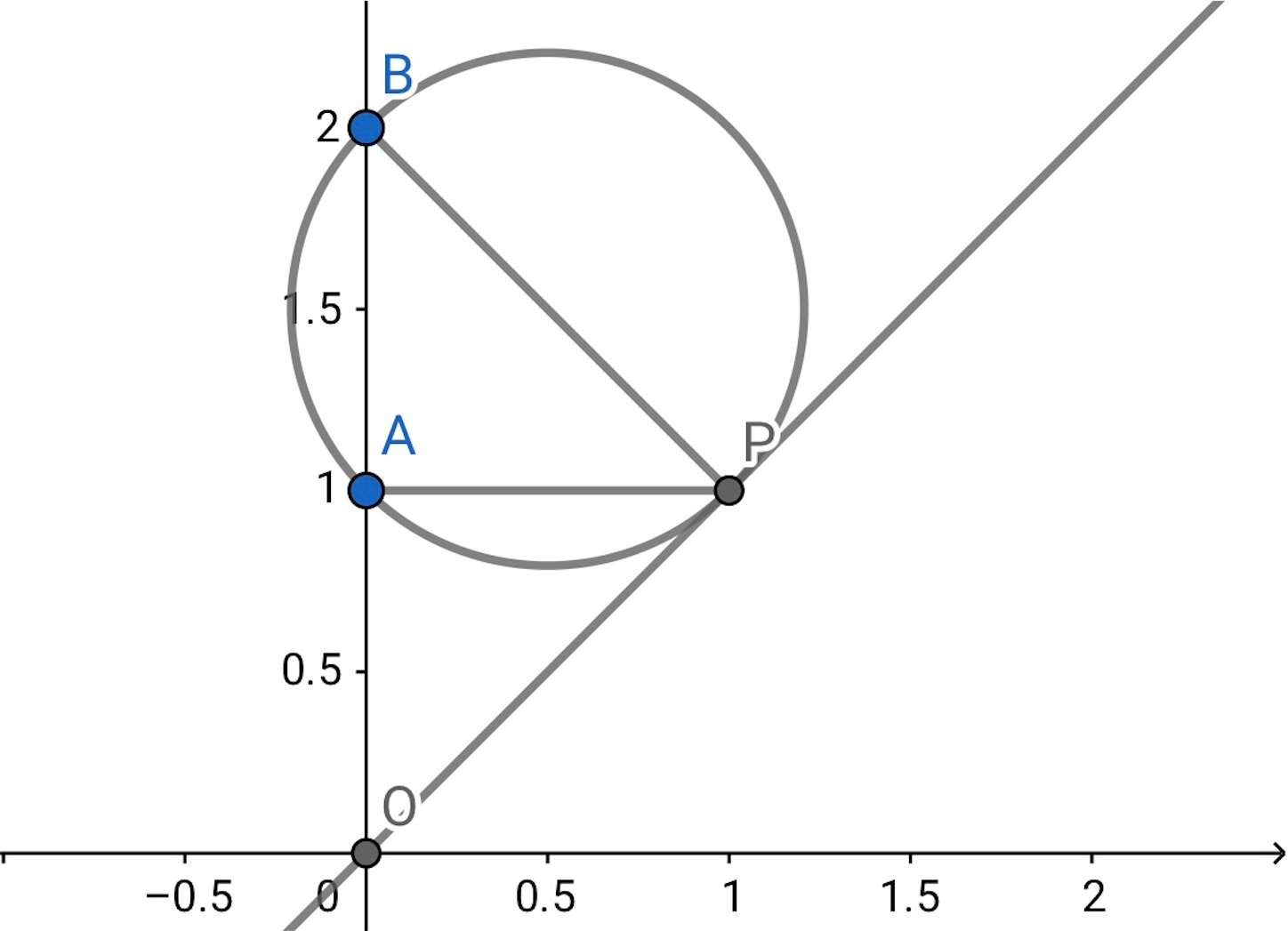
点, 点
を通り,
に接する
つの円のうち, 半径の小さい方を考える *1. すると,
が接点の位置にあるとき題意を満たす. (円周角の定理から. 直線
について接点と同じ側にある
,
上の
を除く点はみな接円の外側にある.)
方べきの定理から,
から,
.
と
は合同なので,
である.
//
※ 記事 では, 与えられた円
に接し, 円外の
点
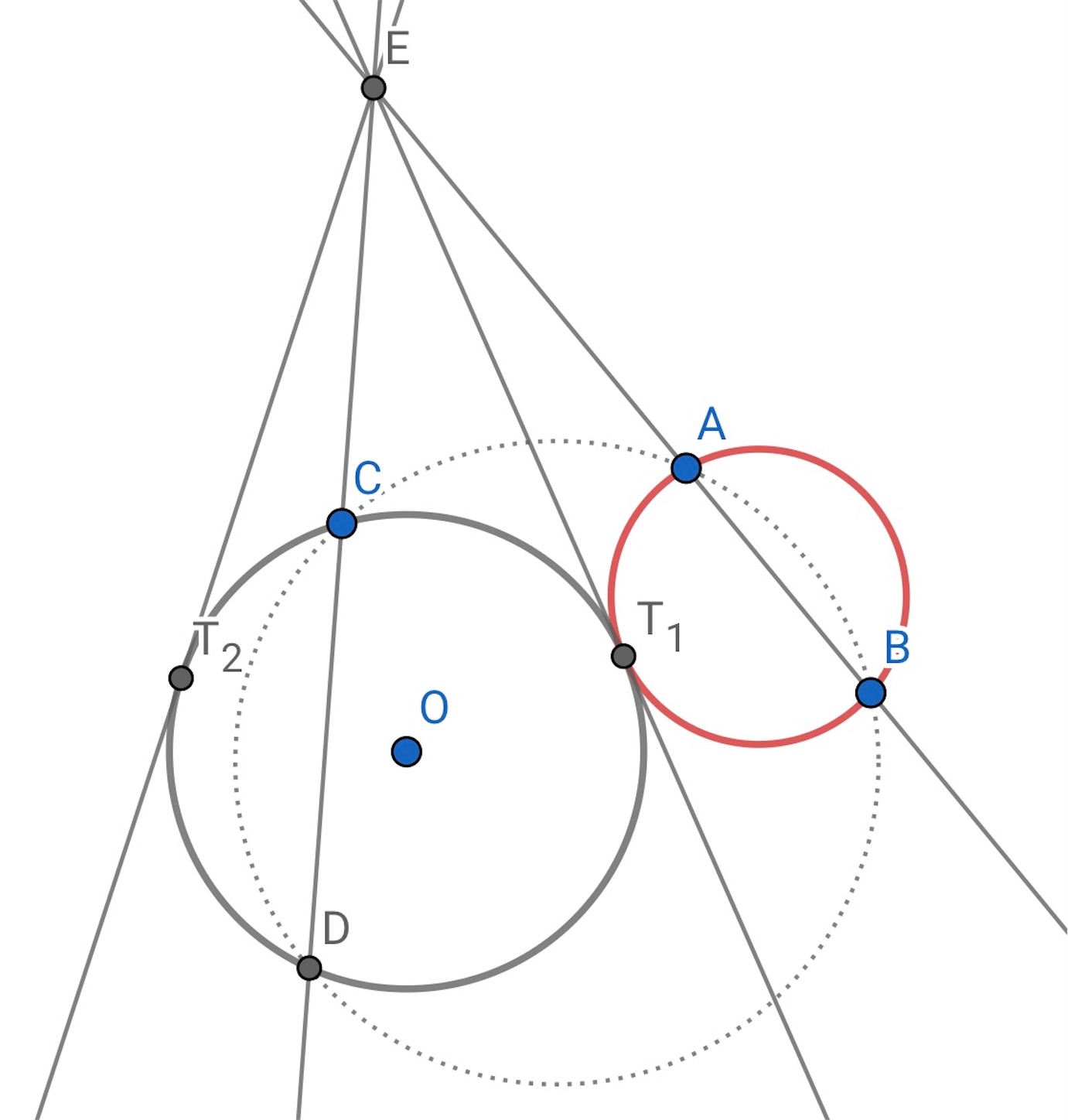
を通る円の作図方法も示したが, 上の問題の観点で, 再度眺めると, 点
が, 円
の周上を動くとき,
を最大にするのが, 円
に外接する方の円の接点 (
) であり (下の最初の図参照),
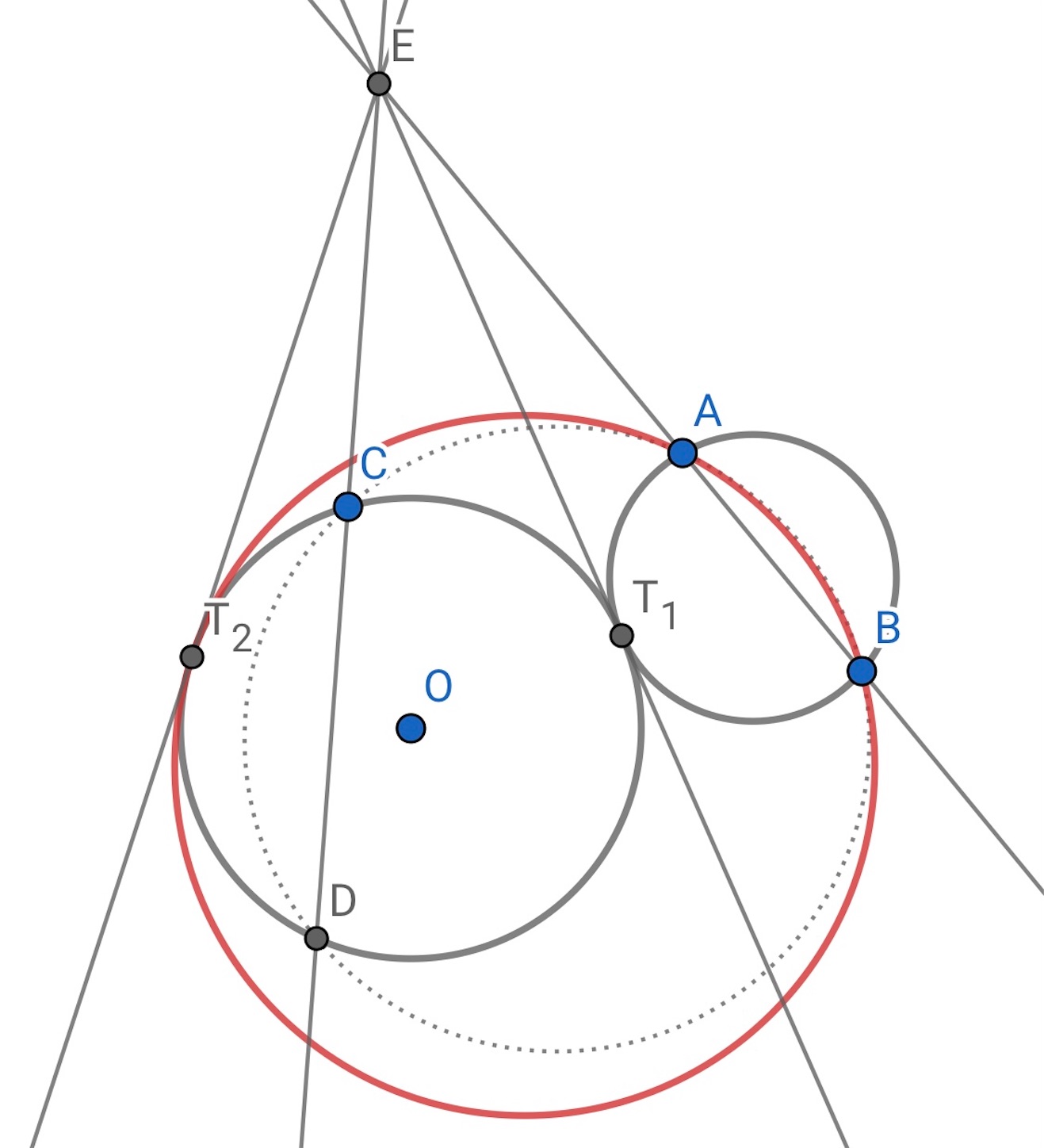
を最小にするのが, 円
に内接する方の円の接点 (
) であることが (下の
番目の図参照), 円周角の定理からわかる. //
*1:詳細は略すが, 半径の大きい方の円の円周角が小さくなることは, 軸 について点
を
に鏡映対称移動し,
であることに留意すれば, 円周角の定理により証明できる.