陥没地帯 (223) - ノリの悪い日記

東京都立高校 2017 年入試問題から. 簡単な問題だけれども, 立体の問題をきちんと説明するのは難しい.

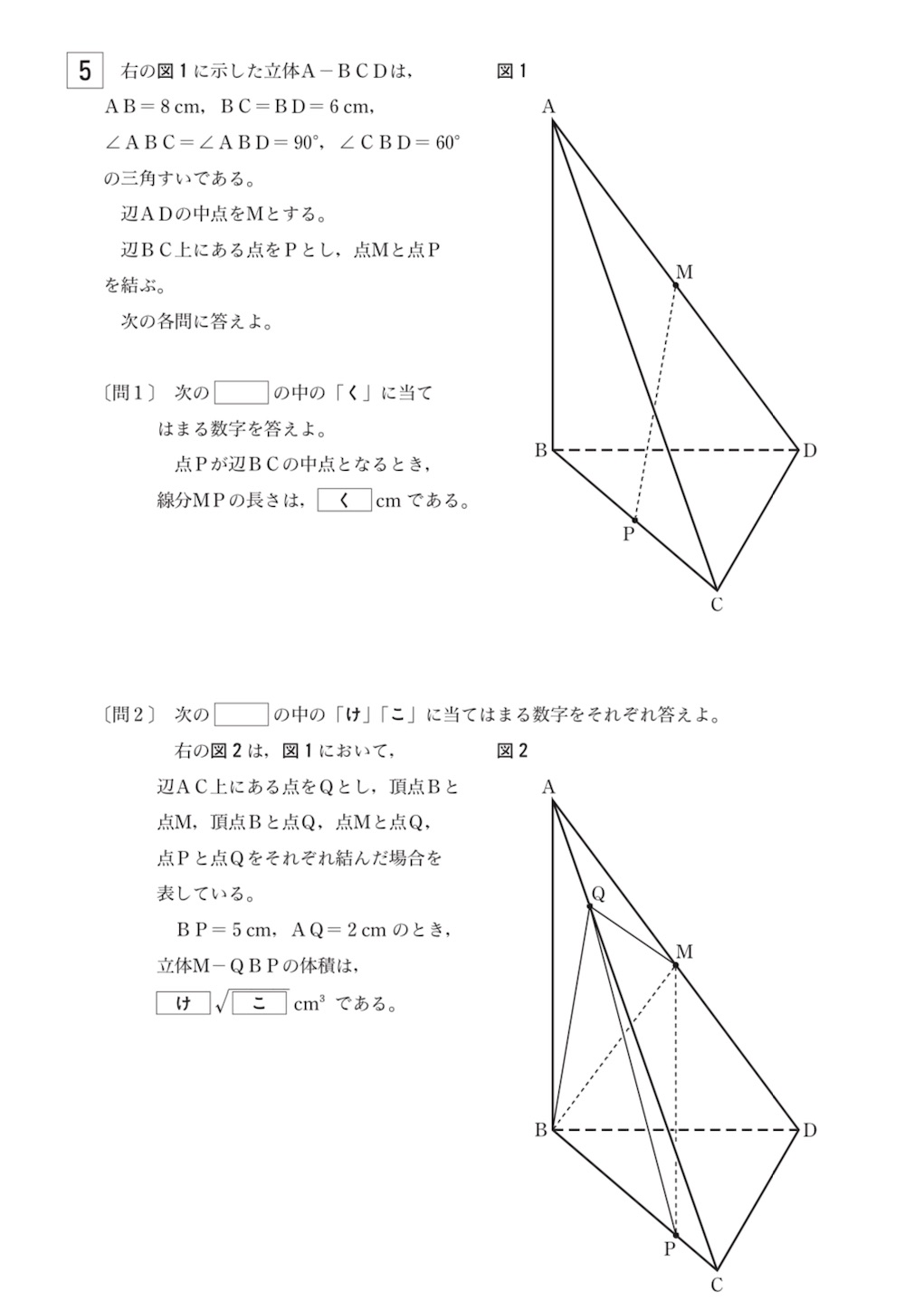
f:id:noriharu-katakura:20210913093614j:plain

問 $(1)$

$MP$ を含む切断面を求めるために, $P$ を通る $AB$ の平行線 $YP$ をひくと, $YP$ は, 平面 $ABC$ 上にある. 理由は前にも述べたように, $AB$ と平行線を含む平面は, $P$ を含むが, $AB$ と $P$ を含む平面はただ一つだからである.

さらに, $YP$ は平面 $ABD$ と平行である. なぜなら, 平面 $ABC$ と平面 $ABD$ の共有点はすべて直線 $AB$ 上に存在するが, $YP$ は $AB$ に平行で平面 $ABD$ と共有点を持たないからである.

直線 $YP$ と $YP$ 上にはない点 $M$ は, 平面をただ一つ決定するが, その平面と平面 $ABD$ の交線 $MZ$ は, 直線 $YP$ と平行である. なぜなら $YP$ と平面 $ABD$ は平行で $YP$ と $MZ$ は, 同一平面上にあるからである.

直線 $MZ$ は, 平面 $ABC$ と平行である. なぜなら $YP$ と $MZ$ を含む平面と平面 $ABC$ の共有点はすべて直線 $YP$ 上に存在するが, $YP$ は直線 $AB$ と平行で, 平面 $ABC$ と平面 $ABD$ の共有点を含まないからである.

直線 $MZ$ と直線 $AB$ はともに平面 $ABD$ 上にあるが, $MZ$ は平面 $ABC$ と平行なので, $AB$ とは共有点をもたない. したがって, 直線 $MZ$ と直線 $AB$ は平行である.

平面上の任意の $2$ 点を結ぶ直線は, その平面にまた含まれるから, 平面 $PYMZ$ に線分 $PM$ は含まれる.

$MZ$ と $AB$ は平行だから, 三角形の相似より, $MZ= 4$ (以下, 単位省略). 中点連結定理より, $PZ= 3$ ( $\triangle BCD$ は正三角形).

$\angle ABC = \angle ABD = 90^\circ$ なので, $AB$ は, 平面 $BCD$ と垂直である. したがって, $AB$ と $PZ$ は, 垂直である. $AB$ と $MZ$ は平行で, $MZ$ と $PZ$ は同一平面にあるから, $MZ$ と $PZ$ は直交する.

したがって, $MP = 5$ である.

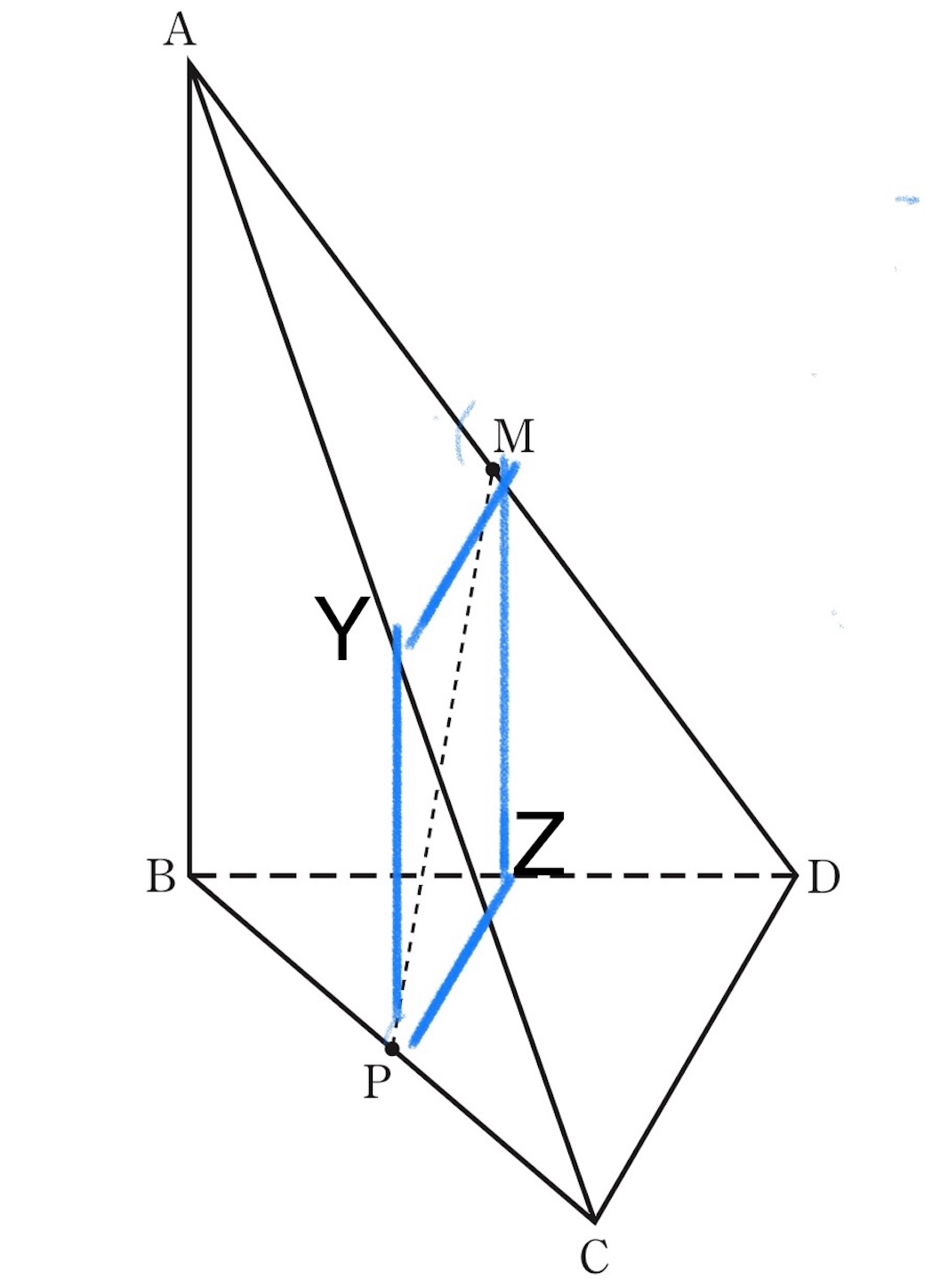
f:id:noriharu-katakura:20210913095432j:plain

問 $(2)$

$\triangle QBP$ の面積は単なる平面図形の問題で $\triangle QBP = 16$ である. 三角錐 $M - QBP$ の高さを求めるために次の定理を証明なしで使う.

定理: 平面に垂直でない直線がその平面上に投ずる正射影は, この直線上の任意の $2$ 点がその平面上に投ずる正射影 *1を結ぶ直線である.

いま, 投影平面として, 平面 $ABC$ を考え, この平面に垂直でない, $AD$ の正射影を考える. そうすると点 $A$ は, $ABC$ と $AD$ の交点だから, $A$ の正射影は, $A$ 自身である.

次に, 点 $D$ から, $BC$ に垂線を下ろすと, 垂線の足は, $\triangle BCD$ が正三角形であることから, $BC$ の中点 (すなわち, 問 $(1)$ における $P$ 点) となる. 直線 $AB$ は平面 $BCD$ と垂直なので, $AB$ は下図の $DP$ と垂直である (あるいは問 $(1)$ の $PY$ と $DP$ は垂直といってもよい). よって, 直線 $DP$ は平面 $ABC$ と直交し, $D$ の平面 $ABC$ における正射影は, 点 $P$ である.

したがって, 前述の定理により, $AD$ が平面 $ABC$ に投ずる正射影は, $AP$ である. 点 $M$ の正射影 $X$ を考えると, 同位角から, $MX$ と $PD$ は平行である. $PD = 3\sqrt{3}$ , $M$ は $AD$ の中点であるから, $MX = 3\sqrt{3}/2$ である.