陥没地帯 (218) - ノリの悪い日記

斜軸回転体の体積を求める有名問題だが, 計算したことがないので, 計算してみる. 立方体の平面による切断面は中学受験から大学受験まで大活躍である. 積分計算自体は, 数 $\mathrm{II}$ 範囲のものである. (実際, 京大は文理共通問題として出題している.)

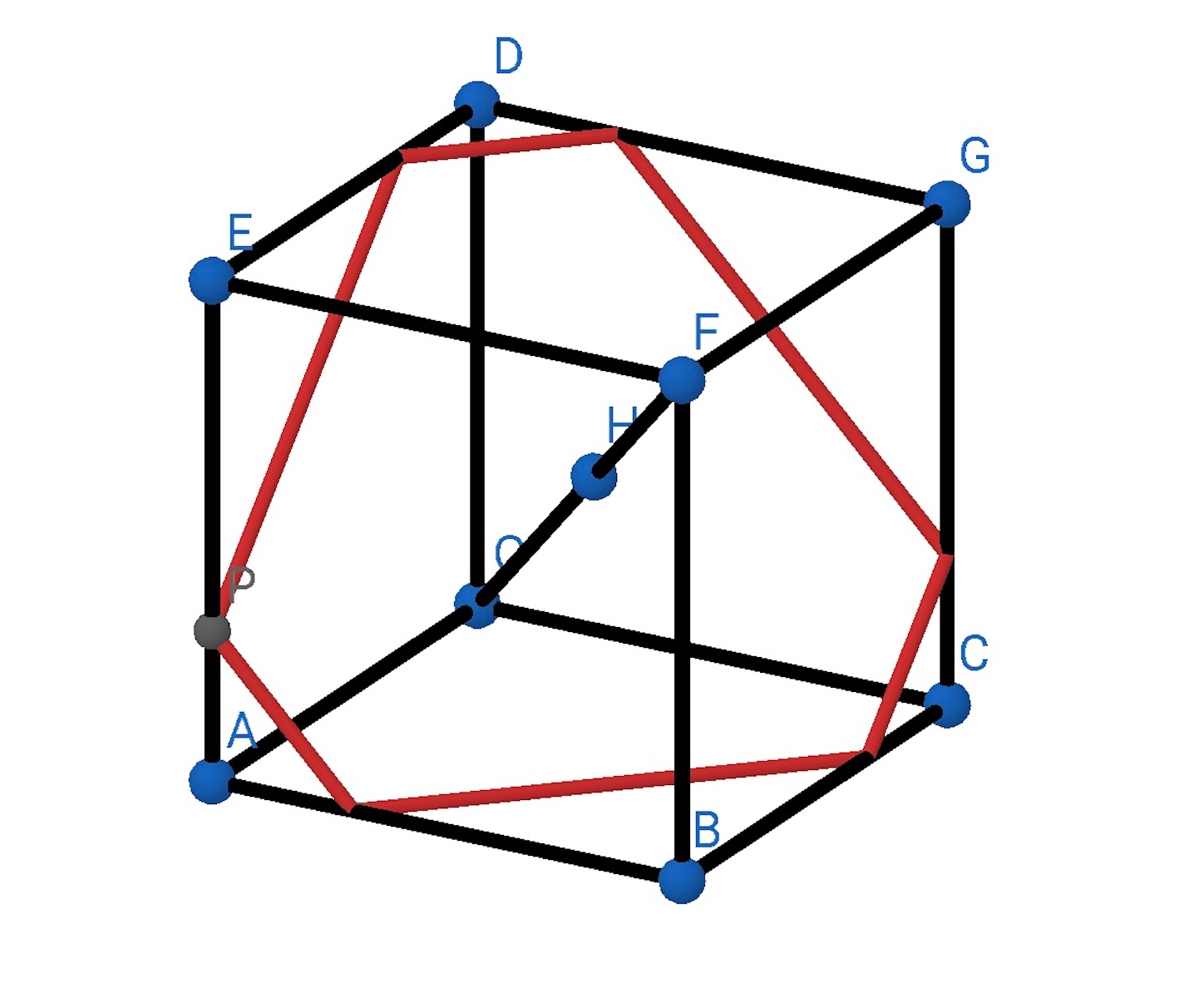
【問】座標空間内で, $O(0,0,0)$ , $A(1,0,0)$ , $B(1, 1,0)$ , $C(0,1,0)$ , $D(0,0,1)$ , $E(1,0,1)$ , $F(1,1,1)$ , $G(0,1,1)$ を頂点にもつ立方体を考える. この立方体を対角線 $OF$ を軸にして回転させて得られる回転体の体積を求めよ.

f:id:noriharu-katakura:20210906222349j:plain

【解】
対角線 $OF$ 上の点を $H(s,s,s)$ ( $0 \leq s \leq 1$ ) とする. $H$ を含み, $OF$ と直交する平面は,

$x + y + z = 3s$

で与えられる*1.

$H$ が $O$ を出発し, 直交面が点 $A$ , $C$ , $D$ を含むまで ( $0 \leq s \leq 1/3$ のとき) は, 直交面は, 線分 $OA$ , $OC$ , $OD$ と交り, 切り口は正三角形となる. この間 ( $0 \leq s \leq 1/3$ ) の回転体は, 回転軸 $OF$ に対して線分 $OA$ を回転させてできる円錐であり, $H(1/3, 1/3, 1/3)$ のとき, 直交面は $A$ を含み, $H$ は $A$ から直線 $OF$ に下ろした垂線の足である.

$\begin{eqnarray} HA^2 &=& (1-1/3)^2 + (1/3)^2 + (1/3)^2\\ &=& \frac{2}{3} \end{eqnarray}$

で,

$\displaystyle{OH = \frac {1}{\sqrt{3}}}$

だから, 円錐の体積は,

$\displaystyle{\frac{1}{3} \pi \cdot HA^2 \cdot OH = \frac{2\sqrt{3}}{27}\pi}$

となる.

次に直交面が点 $E$ , $G$ , $B$ を含むまで ( $1/3 \leq s \leq 2/3$ のとき) は, 切り口は六角形となり, それより後, $H$ が $F$ に達するまで ( $2/3 \leq s \leq 1$ ) は再び正三角形になる. したがって, 対称性から $0 \leq s \leq 1/2$ までの回転体の体積を求めて結果を $2$ 倍すればよい.

切り口が六角形となるとき, $H(s,s,s)$ を含み, 対角線 $OF$ に垂直な平面が, 線分 $AE$ と交わる点 $P$ の座標を求めれば, $P(1,0, 3s-1)$ なので,

$\begin{eqnarray} HP^2 &=& (1-s)^2+s^2+(2s-1)^2\\ & =& 2(3s^2 -3s +1) \end{eqnarray}$

となる (その他の辺の交点と $H$ の距離も同じになる. 最小値は, $s = 1/2$ のときで, このとき切り口は正六角形になる).

したがって, $1/3 \leq s \leq 1/2$ のときの回転体の体積は, $OH = t$ とおくと, $t =\sqrt{3}s$ , $dt = \sqrt{3}ds$ であるから,

$\displaystyle{ \int_{1/3}^{1/2}\pi \cdot HP^2(\sqrt{3}ds)\\ =2\sqrt{3}\pi \int_{1/3}^{1/2}(3s^2-3s+1)ds \\ = 2\sqrt{3}\pi \left[ s^3-\frac{3}{2}s^2 + s \right ]_{1/3}^{1/2}\\ = \frac{5\sqrt{3}}{54}\pi }$