ノリの悪い日記

古今東西の映画、ポピュラー音楽、その他をいまここに交錯させながら随想します。

ノリの悪い日記 https://www.port-k.com

陥没地帯 (213)

初等幾何

Overleaf を使わせてもらって, テキストを作るのに忙しかったのでブログは暫くお休みしていた.

記事 ( $188$ ) を書いてから, その後を書いていなかった. 記事 ( $188$ ) では以下の証明まで終わっている.

$\triangle ABC$ の内心を $I$ とする. また $\triangle ABC$ の外接円の半径を $R$ , 内接円の半径を $r$ とする. $AI$ の延長が, 外接円の周と交わる点を $D$ とすれば,

$AI \cdot ID= 2Rr$

である.

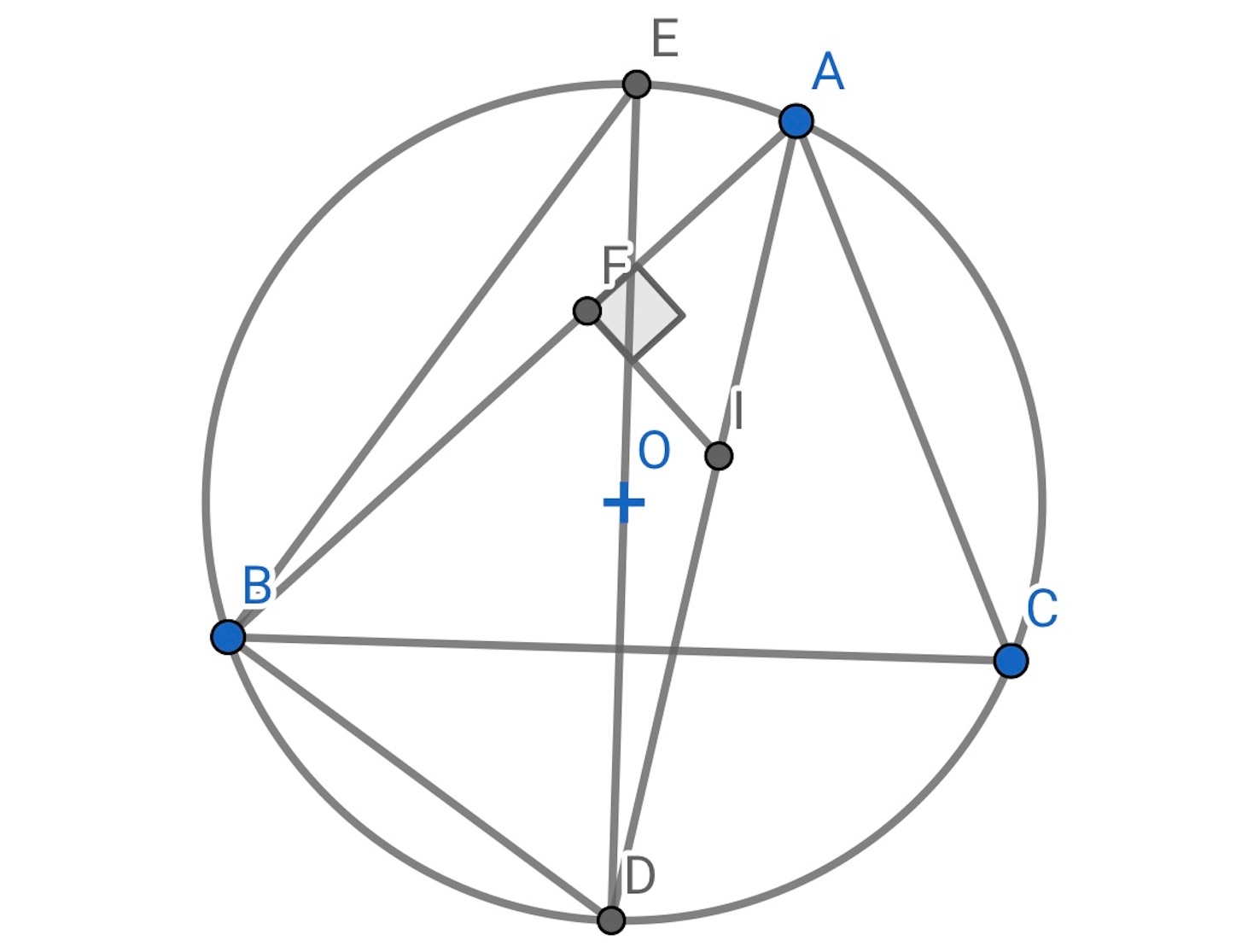
f:id:noriharu-katakura:20210601144438j:plain

外心を $O$ とすると, 方べきの定理から,

$\begin{eqnarray} OI^2 - R^2 &=& -AI \cdot ID\\ &=& -2Rr \end{eqnarray}$

となって, いわゆるオイラー・チャップルの定理が得られる.

オイラー・チャップルの定理から, $R \geq 2r$ が成りたつこともすぐにわかる. 等号が成立するのは, $OI = 0$ のとき, すなわち三角形が正三角形となるときである. もっとも, この不等関係は, 前の記事から, $9$ 点円とは, 三角形の各辺の中点を結んだ三角形の外接円で, その半径は, $R/2$ だったことからすでにわかっていたことである. つまり, もとの三角形の $3$ 辺と交わる円は, 明らかに内接円の半径より大きいので, $R \geq 2r$ である.

ポンスレの閉形定理は以下のようになる.

$2$ 円 $O$ , $I$ があるとき, 円 $O$ に内接し, 円 $I$ に外接する三角形が $1$ つあれば, このような三角形は無数にある.

f:id:noriharu-katakura:20210720014627j:plain

円 $O$ の周上の任意の点を $A'$ とする. 直線 $A'I$ が円 $O$ の周と交わるもうひとつの点を $M$ とする. $M$ を中心として, 半径 $MI$ の円が, 円 $O$ の周と交わる点を $B'$ , $C'$ とする.

$A'M$ は明らかに $\angle A'$ の $2$ 等分線である.

$\begin{eqnarray} \angle A'B'C' &=& \angle A'MC\\ &=& 2\angle IB'C' \end{eqnarray}$

だから, $IB'$ は $\angle B$ の $2$ 等分線である.

したがって, $I$ は, $\triangle A'B'C'$ の内心でもある. $\triangle A'B'C'$ の内接円の半径を $r'$ とすると, オイラー・チャップルの定理から,

$\displaystyle{OI^2 = R^2 - 2Rr'}$

となるが,

$\displaystyle{OI^2 = R^2 - 2Rr}$

でもあるので, 結局,

$r' = r$

である. $A'$ は円 $O$ の円周上の任意の点であるから, このような三角形は無数にある. //