陥没地帯 (211) - ノリの悪い日記

前回の記事の最後に引き続いて, 相似変換 (中心相似) の応用を少しやってみる.

定円 $O$ 内に定点 $P$ をとり, $P$ を通る弦 $AB$ を引いて $AP: PB = 2:3$ とせよ, という作図問題を考えてみる.

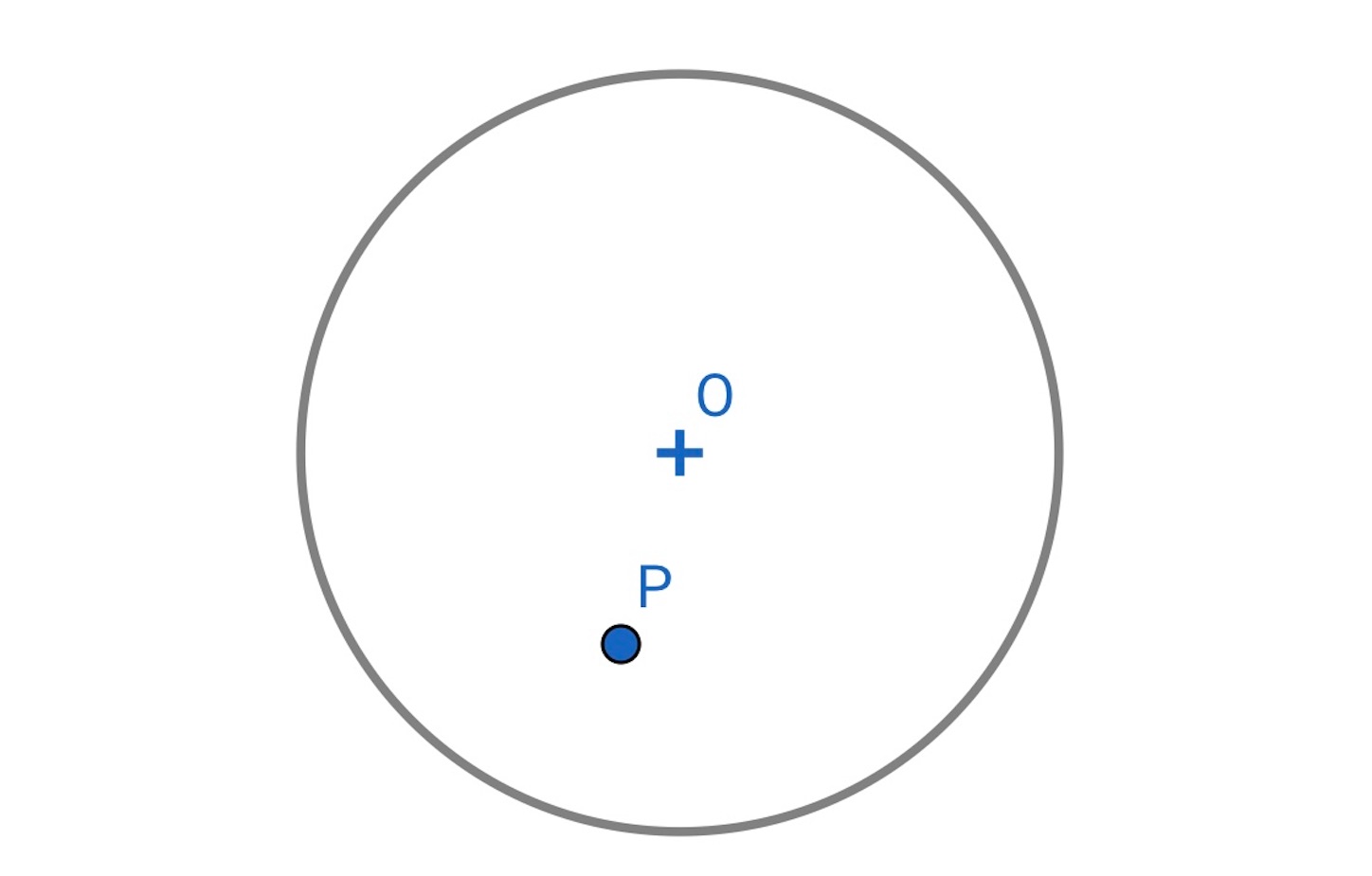
f:id:noriharu-katakura:20210711155941j:plain

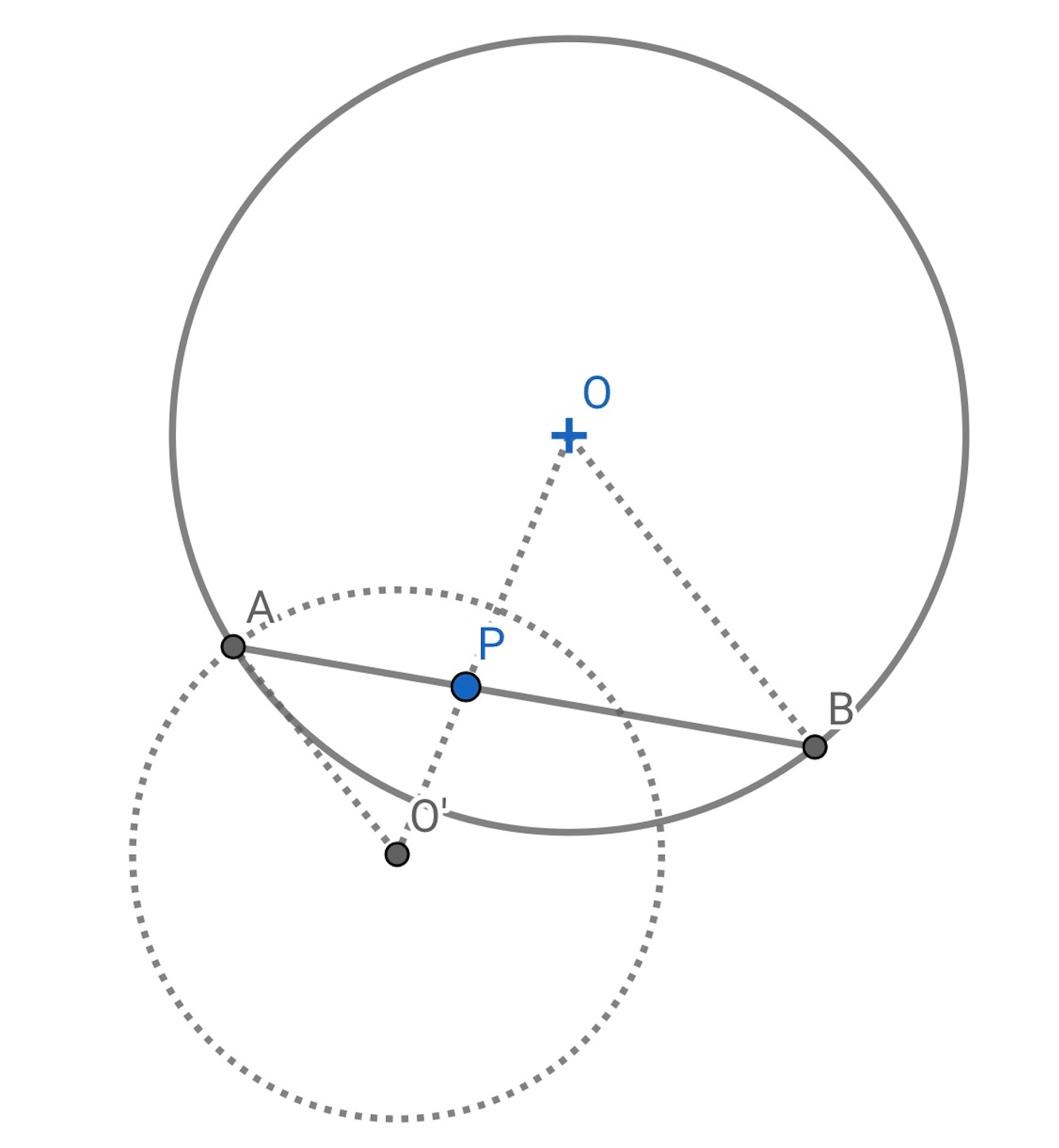
作図の解析をするために, 条件をみたす弦 $AB$ が引けたと考えると, $P$ を相似の中心として, $O'P: OP=2:3$ , $AO': OB = 2:3$ であるから, $A$ は円 $O'$ の周上の点でもある. したがって, 作図としては, $\displaystyle{ PO' = \frac{2}{3}OP}$ となるように, $OP$ の延長上に点 $O'$ をとり, $O'$ を中心に半径が円 $O$ の半径の $2/3$ となるような円 $O'$ を描いて, 円 $O$ の $2$ つの交点のどちらかを $A$ とすればよい.//

f:id:noriharu-katakura:20210711160252j:plain

$O$ を中心とする二つの同心円がある. $1$ つの直線を引いて, 外円の弦 $AD$ を内円の弦 $BC$ の $2$ 倍となるようにせよ.

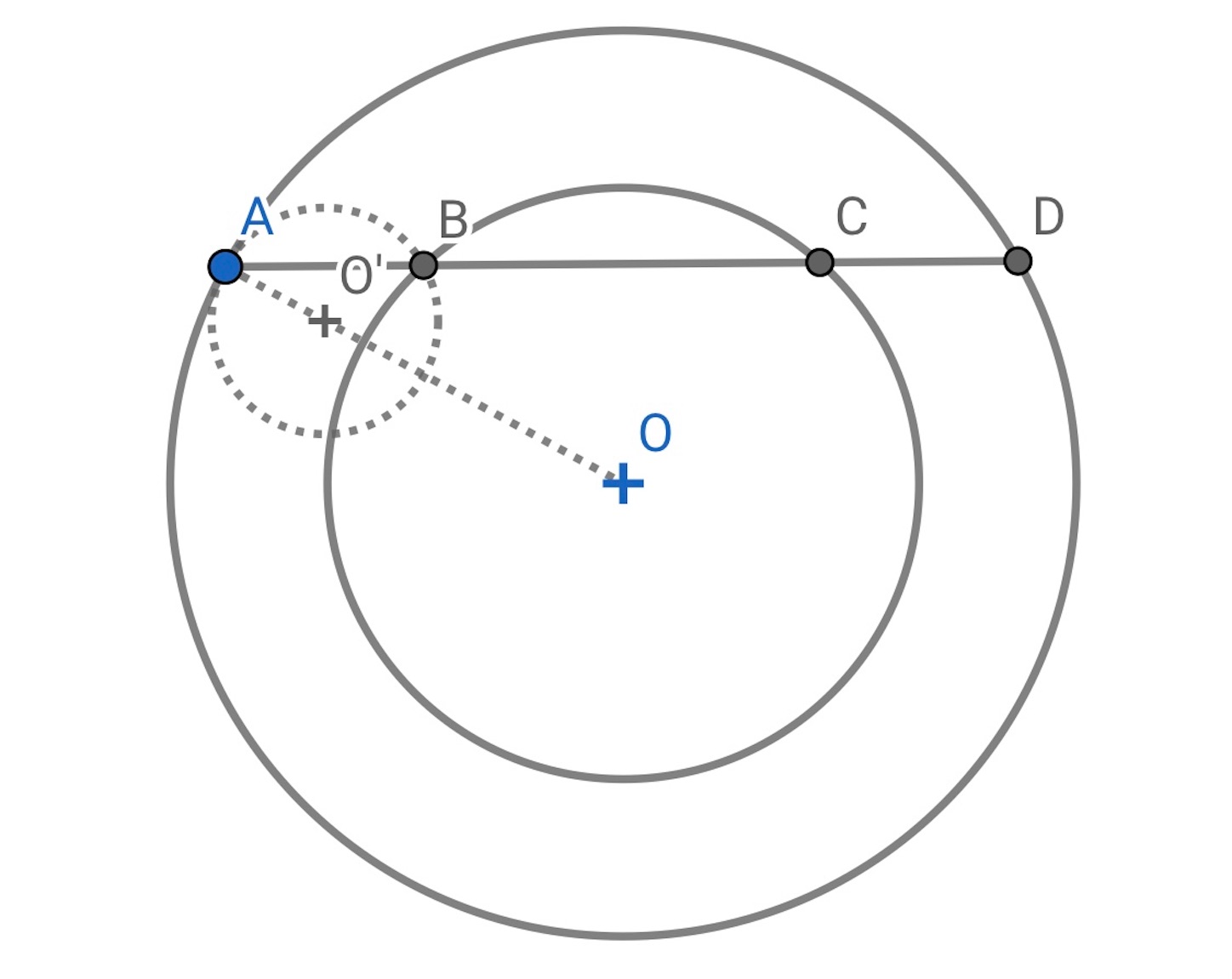
f:id:noriharu-katakura:20210711172126j:plain

$AB: AD = 1:4$ ということだから $A$ を相似の中心とし, 半径が外円の半径の $1/4$ の円 $O'$ を描けばよい.//

以下は, 前の記事と似たような作図なので説明は不要だろう.

与えられた三角形 $ABC$ の辺 $AB$ , $BC$ , $CA$ 上にそれぞれ, 点 $P$ , $Q$ , $R$ を求めて,

$PR \perp AC$ , $RQ \perp BC$ , $QP \perp AB$

となるようにせよ.

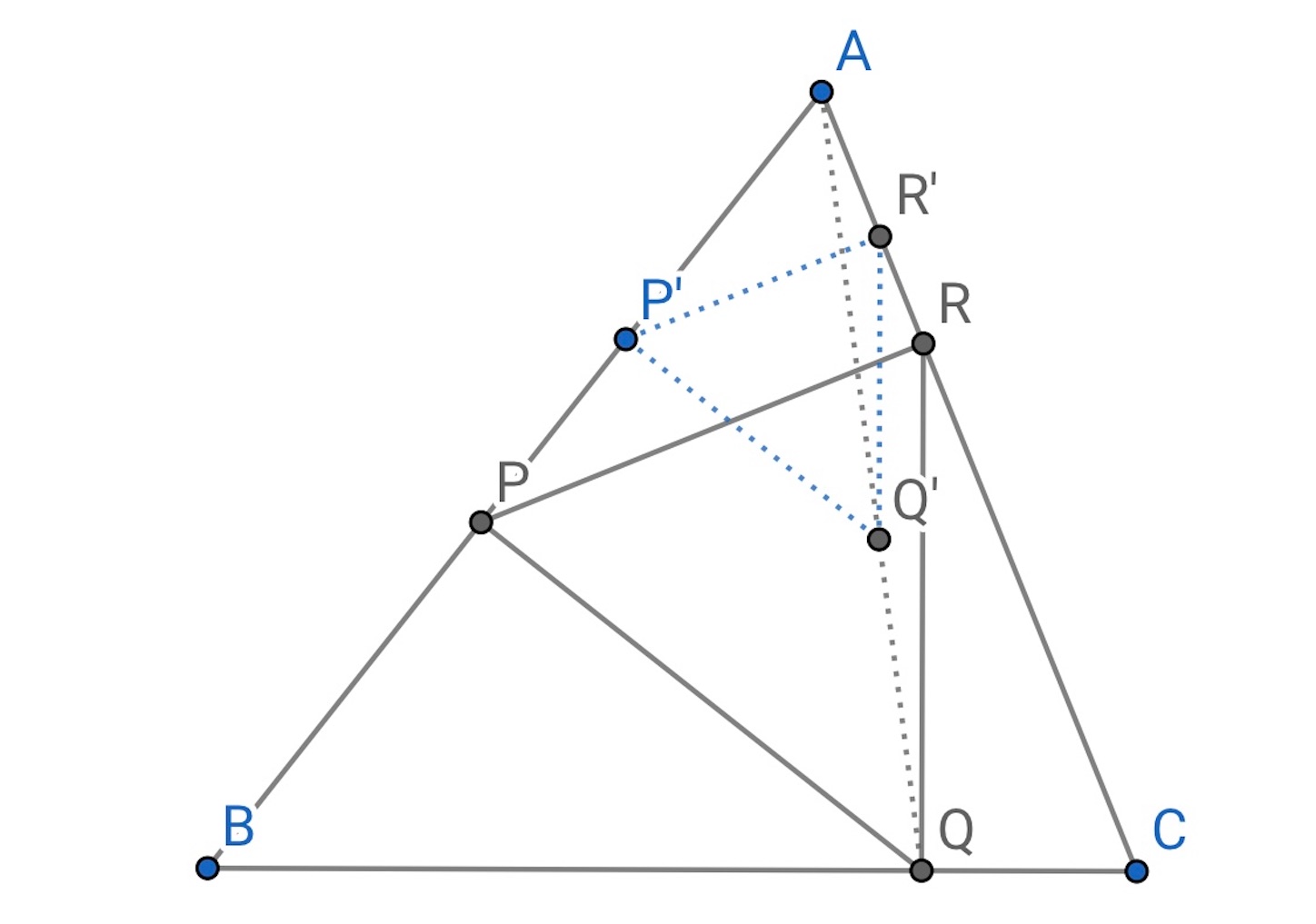
f:id:noriharu-katakura:20210711181613j:plain

他にもこんな例がある.

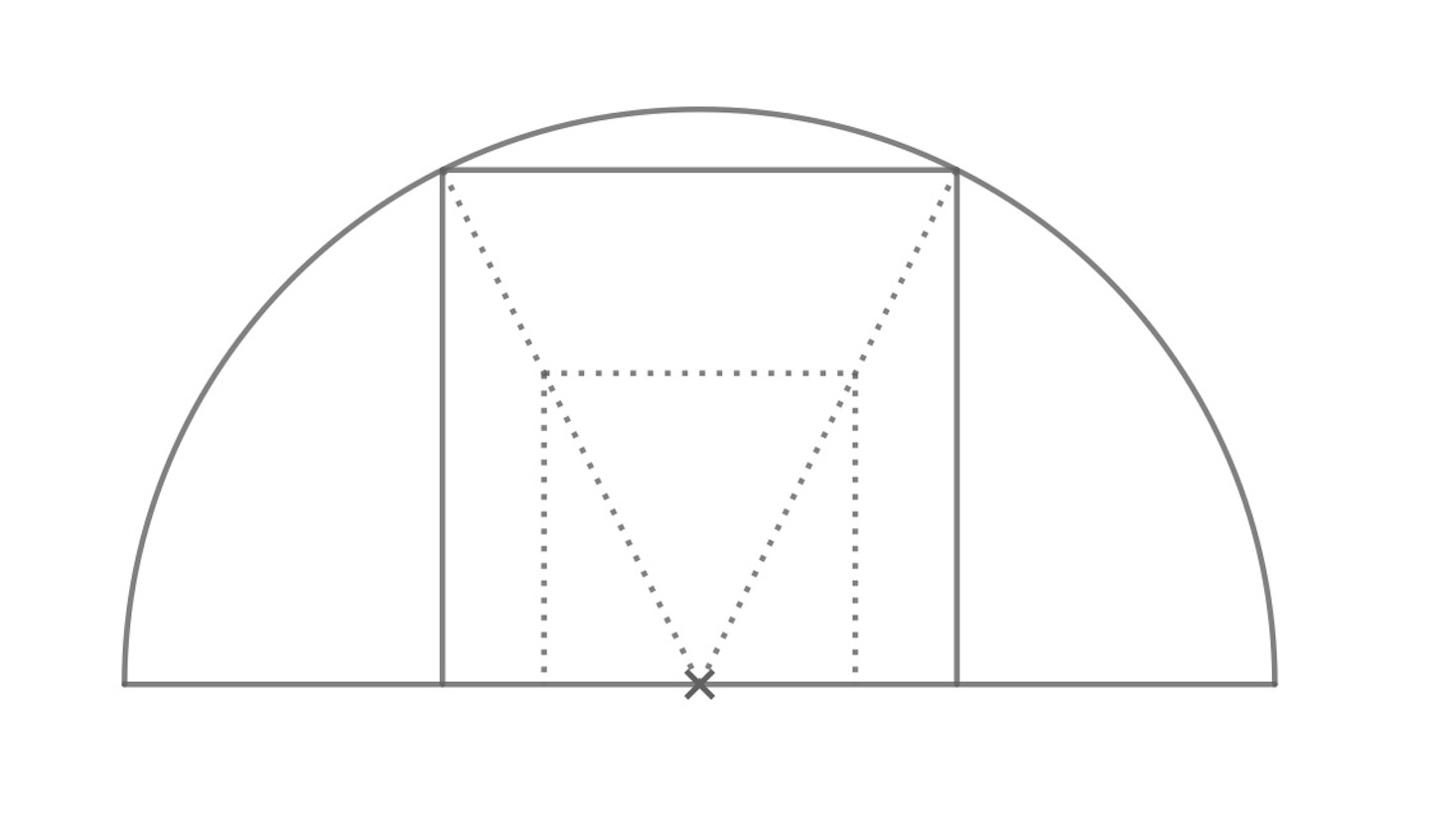
f:id:noriharu-katakura:20210711191820j:plain

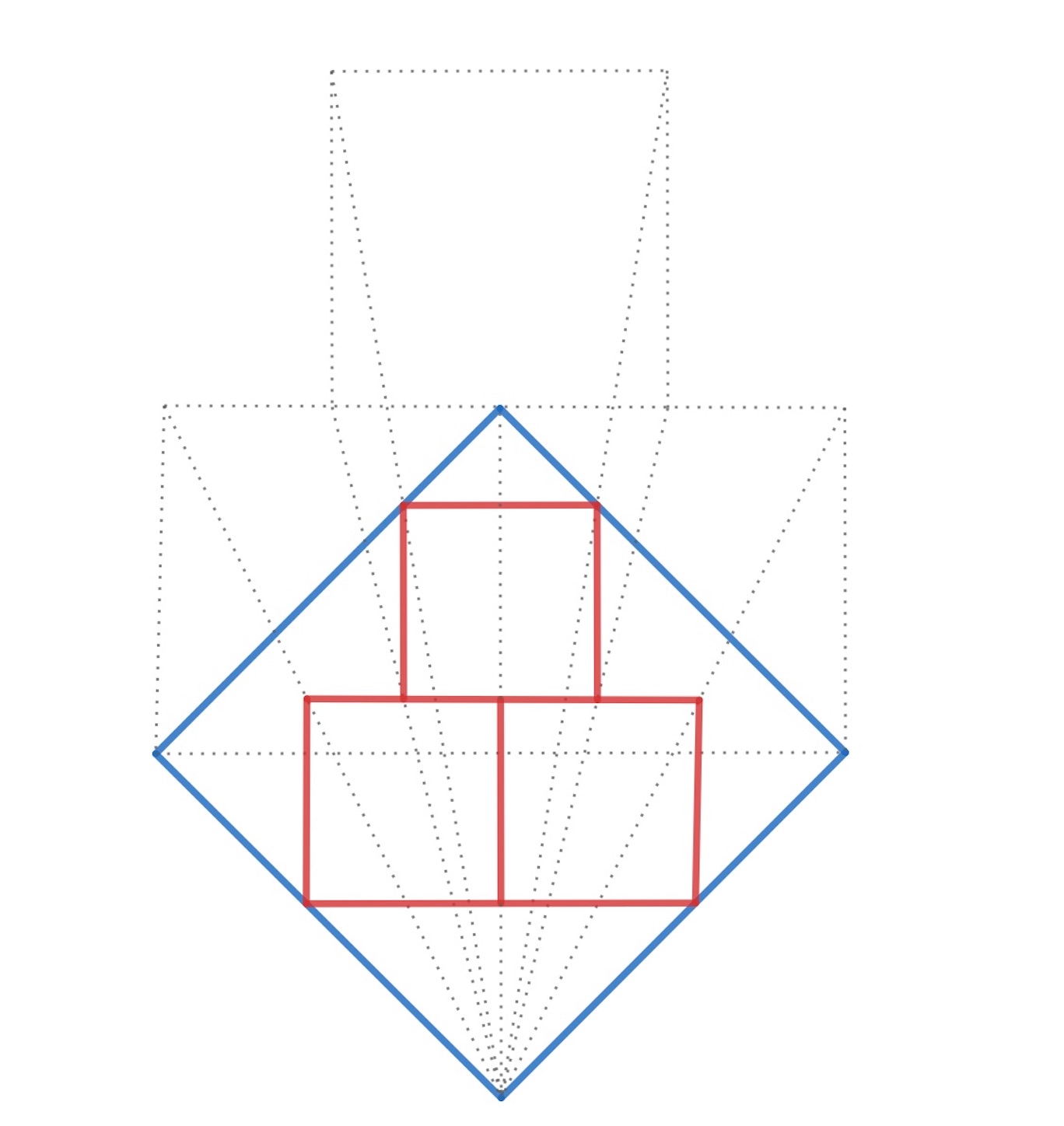
f:id:noriharu-katakura:20210711195020j:plain

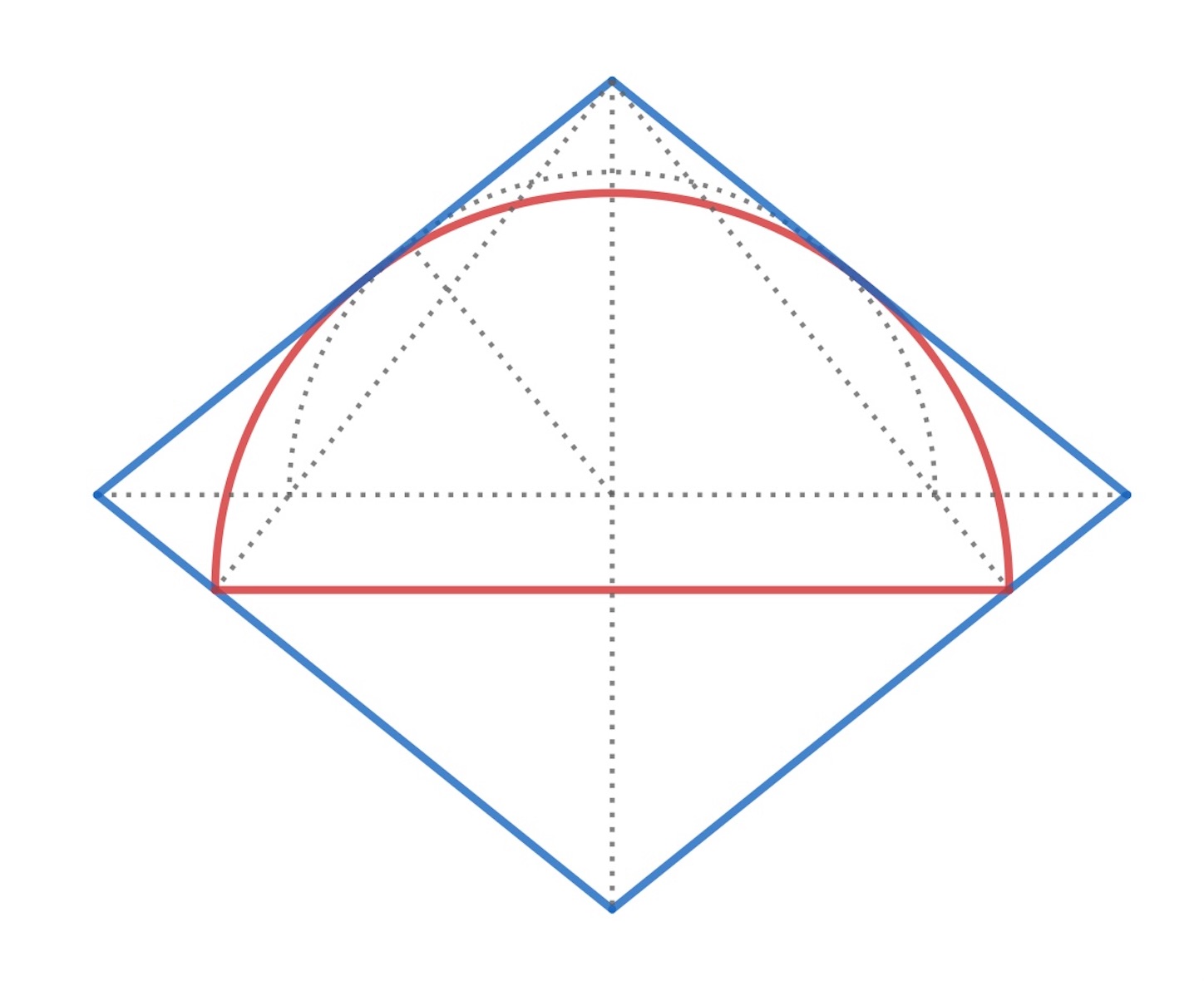
f:id:noriharu-katakura:20210711202210j:plain
//

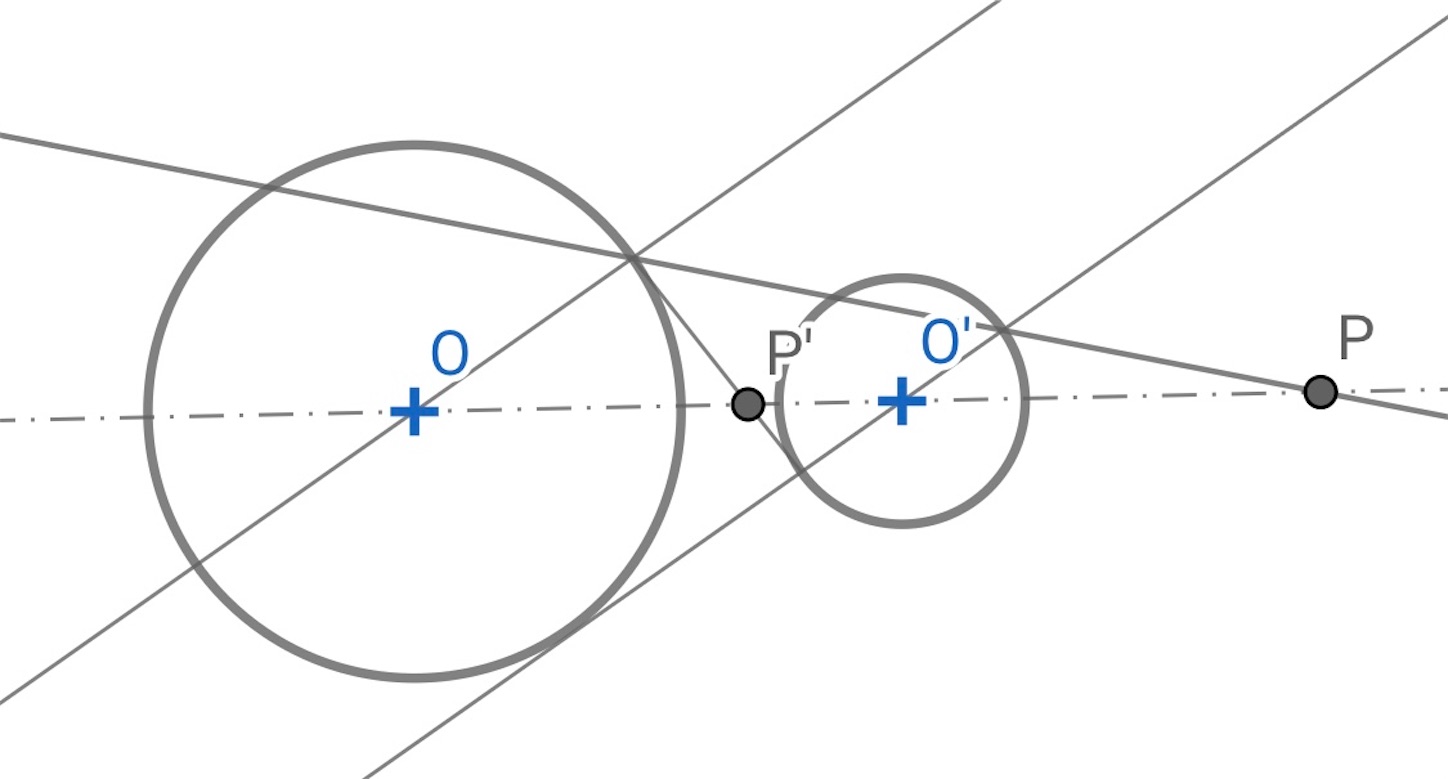
円の共通接線を引く作図も, よく紹介されているものより, 下の図のようにして, $2$ つの相似の中心 *1 を先に求めてしまった方が楽だと思う. $2$ つの円の相似の中心とは, $2$ つの円の中心を結ぶ線分を円の半径の比に外分, 内分する点のことであり (つまり, $O$ , $P'$ , $O'$ , $P$ は調和点列をなす), 等しくない $2$ 円に共通接線が引ける場合には, 相似の中心を通る片方の円の接線を引けば, もう一方の円にも必ず接する, つまりその接線は共通接線となる. また, 相似の中心を通る直線が $2$ つの円の割線となるとき, 対応するそれぞれの円弧の円周角は等しくなることにも注意したい.//

f:id:noriharu-katakura:20210711205554j:plain

正三角形を除く三角形の外心 $O$ , 重心 $G$ , 垂心 $H$ はオイラー線と呼ばれる同一直線上にあり, $G$ は線分 $OH$ を $1:2$ の比に内分することはよく知られている.

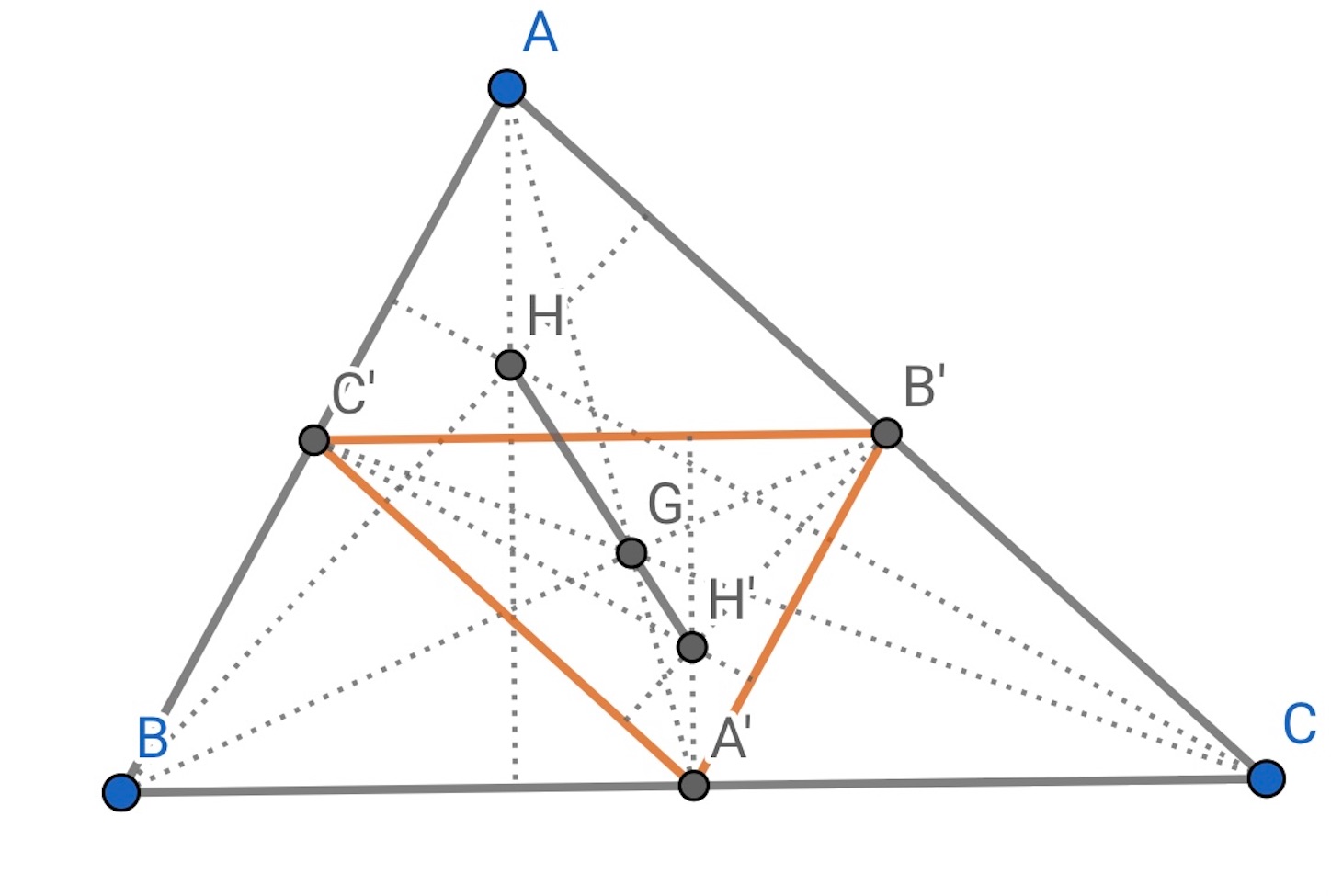
f:id:noriharu-katakura:20210712121224j:plain

$A'$ , $B'$ , $C'$ は $\triangle ABC$ の重心 $G$ を中心とし, $A$ , $B$ , $C$ をそれぞれ相似比 $-1/2$ で中心相似変換したものだから, $\triangle ABC$ と $\triangle A'B'C'$ は相似の位置にある (したがって $\triangle ABC$ と $\triangle A'B'C'$ は相似である). ところが, $\triangle A'B'C'$ の垂心 $H'$ は, $\triangle ABC$ の外心 $O$ と一致する. よって題意が成立する.//

*1:ただし、 $2$ つの円が等円または同心円の場合には, 相似の中心を $1$ つしかもたない. 等円の場合の相似の中心は円の中心を結ぶ線分の中点であり, 同心円の場合は中心に一致する.