陥没地帯 (209) - ノリの悪い日記

初等数学において論理的思考力や発見力や創造力をつけるということは, ほとんど幾何を学ぶことと同値であるみたいな意見をいろいろと読んでいると, じゃあ幾何は呆け予防にもなるのかなあと, 不図思ってしまう.

前回記事の算額の別解を反転 *1 を用いて与えておくことにした. その前に準備として, 反転の関係にある二つの円の一方の半径がわかったとき,他方の半径を求める式を求めておく.

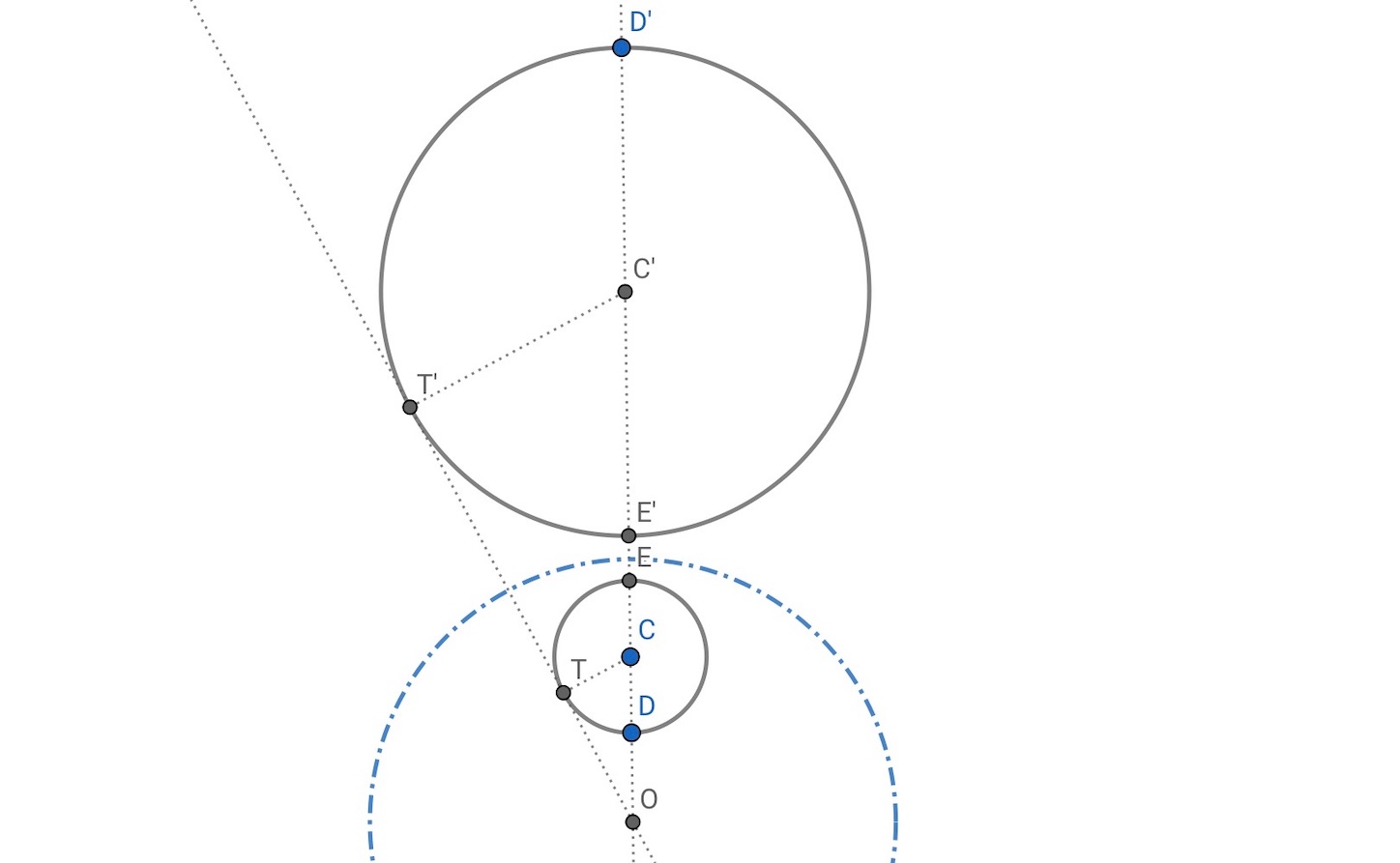
f:id:noriharu-katakura:20210709160635j:plain

上の図で $O$ は反転の中心で, 反転円の半径を $k$ としておく.

$\begin{align} OD \cdot OD' &= k^2\\ OE \cdot OE' &= k^2 \end{align}$

から, 円 $C'$ の半径 $r'$ は, 円 $C$ の半径 $r$ を使って,

$\begin{eqnarray} r' &=& \frac{OD' -OE'}{2}\\ &=& \frac{k^2}{2}\left(\frac{1}{OD}-\frac{1}{OE}\right)\\ &=& \frac{k^2}{2}\cdot \frac{OE-OD}{OD\cdot OE} \\ &=& \frac{k^2}{OT^2}r \end{eqnarray}$

最後は方べきの定理からで,

$OT^2 = OC^2 - r^2$

であることはすでにやった.

$OT\cdot OT' = k^2$

だから, 円 $C$ の半径 $r$ は, 円 $C'$ の半径 $r'$ を使って,

$\begin{eqnarray} r &=& \frac{OT^2}{k^2}r'\\ &=& \frac{k^2}{OT'^2}r' \end{eqnarray}$

である.//

前回の問題をもう一度記載しておくと, 図のような中心角 $120^\circ$ の扇形で, 下側の $2$ 番目に小さい $2$ つの円の半径が与えられたとき, 上側の一番小さい $2$ つの円の半径を求めよというものである.

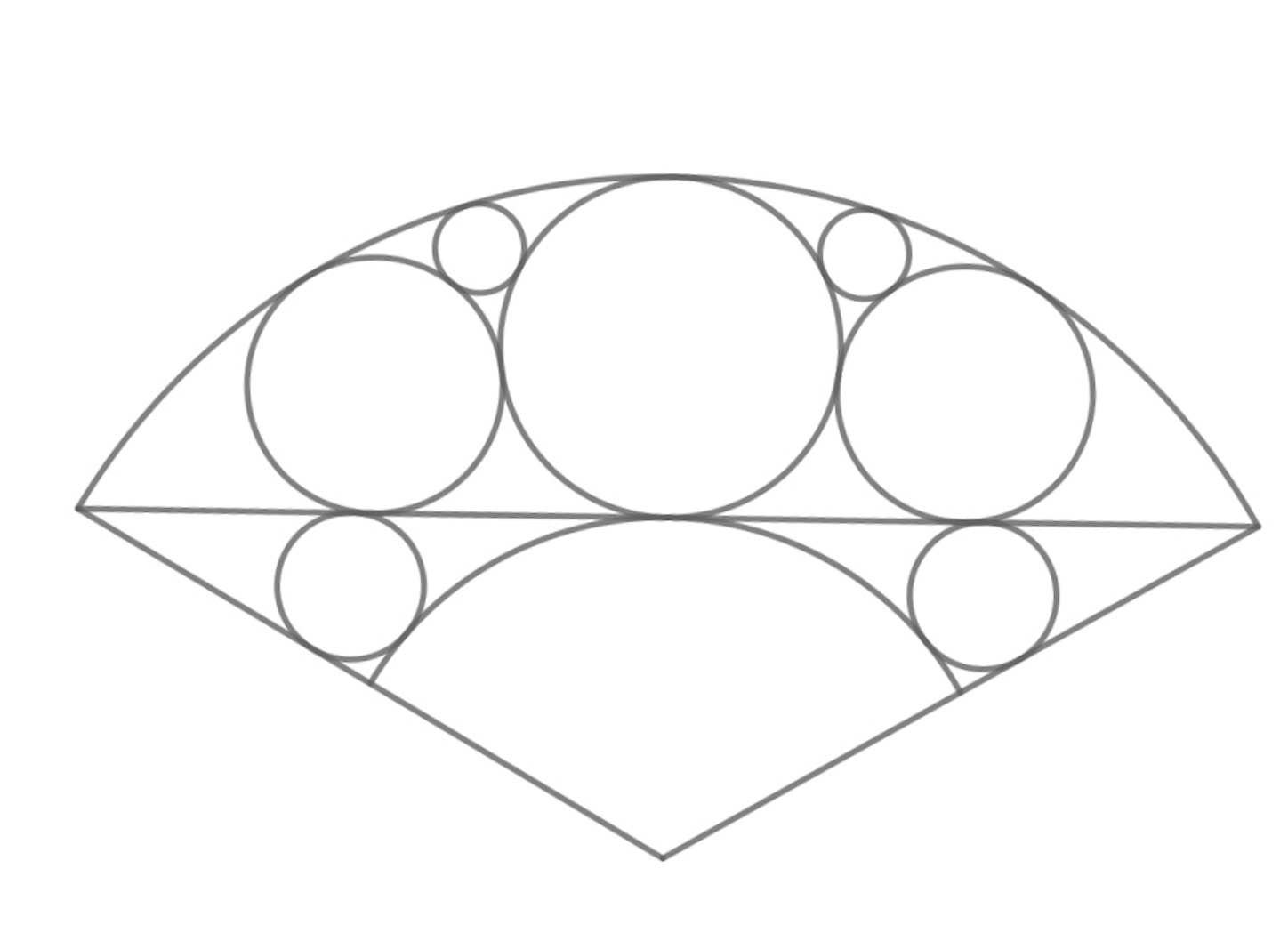
f:id:noriharu-katakura:20210705020850j:plain

前回の記事との重複を避けるために, $AQ = R$ として, 円 $E$ , $W$ の半径はそれぞれ,

$\begin{align} r_E &= \frac{1}{4}R\\ r_W &= \frac{3}{16}R \end{align}$

ですでに求められているものとし, 円 $N$ の半径を $R$ で表わすことにする. 反転の中心は, 下図の $O$ にとり, 反転円の半径は, $2R$ である.

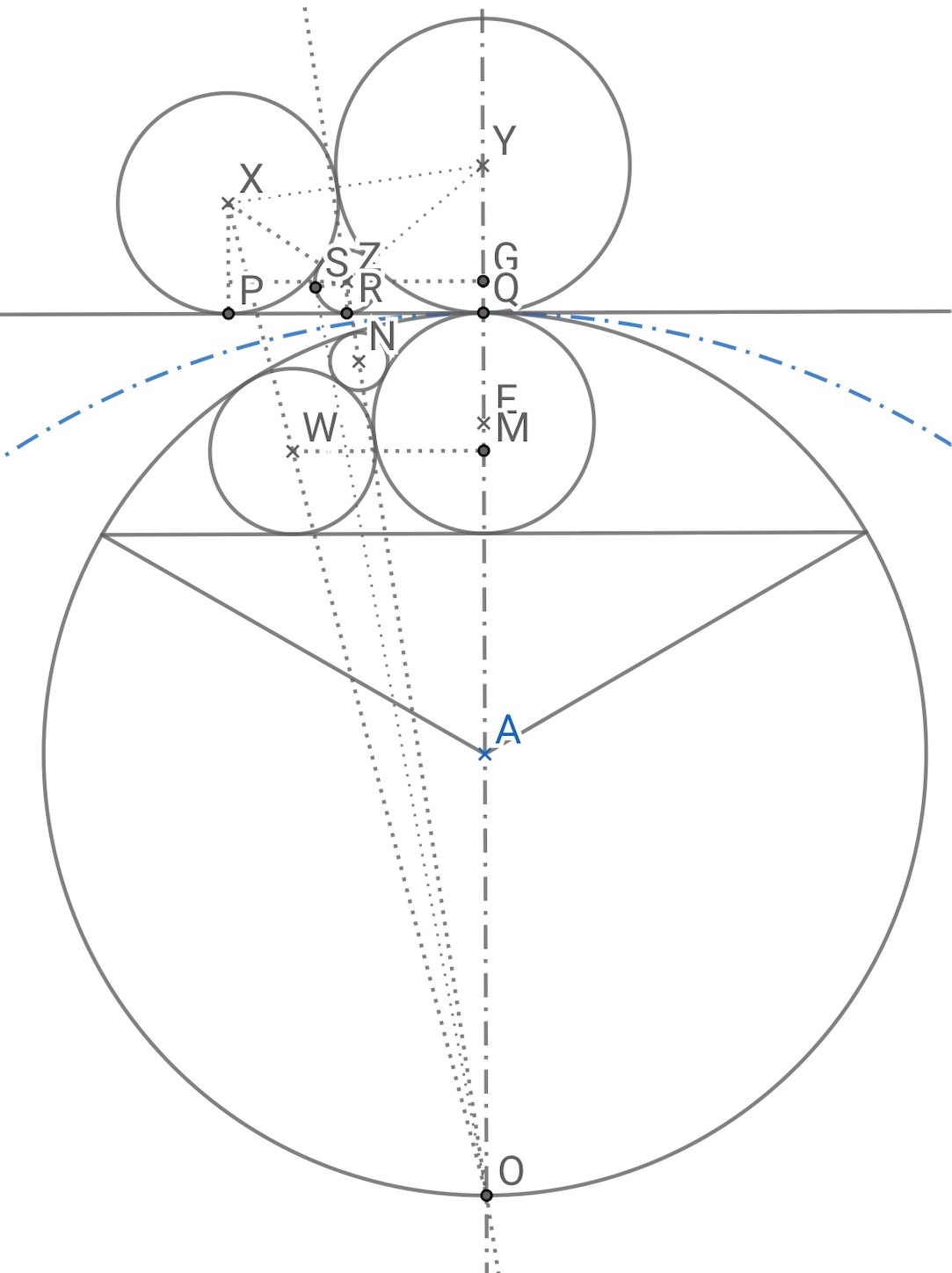
f:id:noriharu-katakura:20210709200619j:plain

下図は, 上図の部分拡大図である.

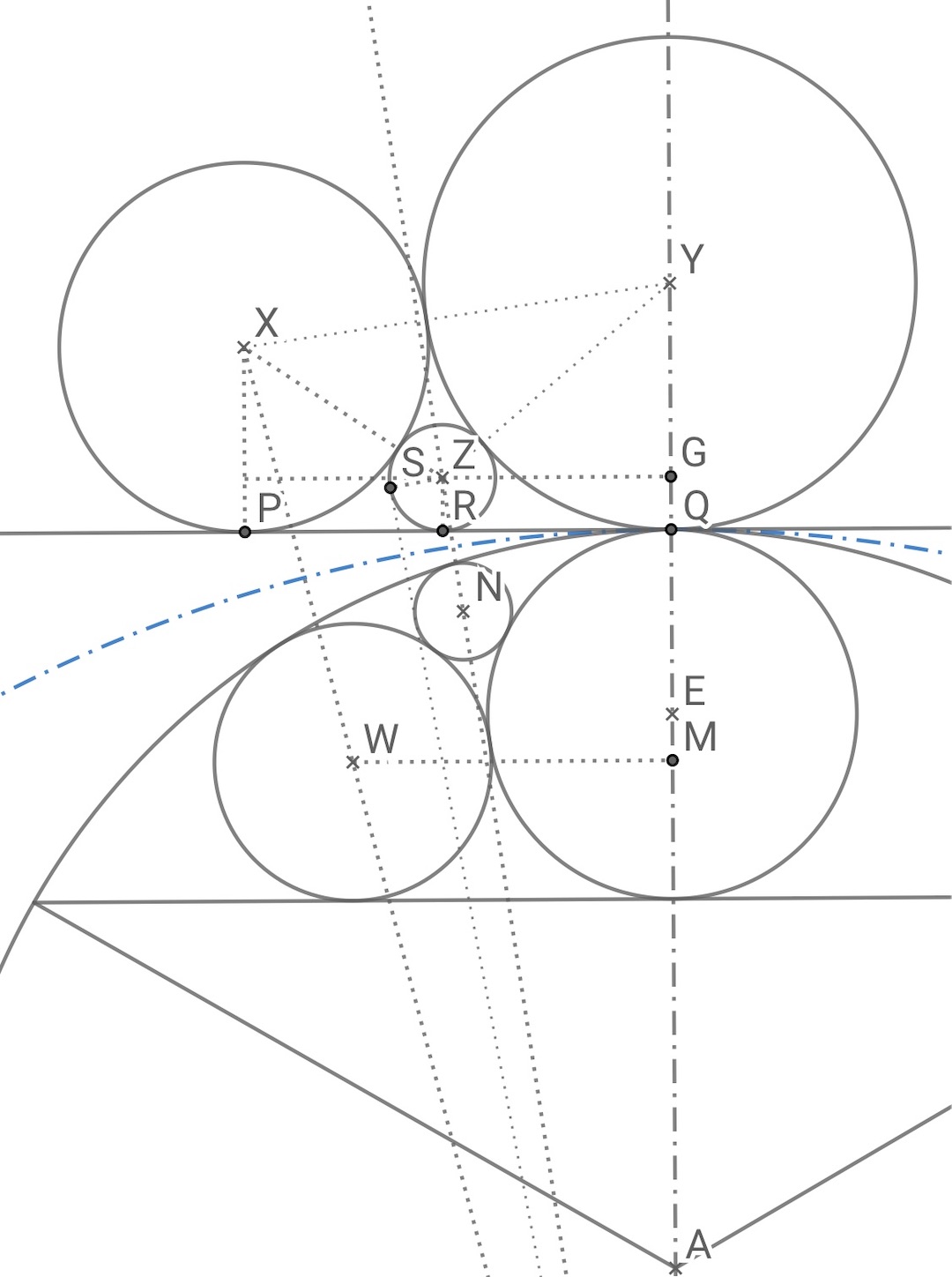
f:id:noriharu-katakura:20210709231912j:plain

まず, 円 $E$ の反形である円 $Y$ の半径 $r_Y$ は,

$\begin{align} OE^2 - r_E^2 &= \{(7/4)^2-(1/4)^2\}R^2 \\ &= 3R^2 \end{align}$

から,

$\displaystyle{r_Y = \frac{4R^2\cdot \frac{R}{4}}{3R^2}= \frac{1}{3}R}$

次に、円 $W$ の反形である円 $X$ の半径 $r_X$ は,

$\displaystyle{ OW^2 - r_W^2 \\ = \{(\sqrt{3}/4)^2+(27/16)^2-(3/16)^2\}R^2 \\ = 3R^2 }$

から,

$\displaystyle{r_X = \frac{4R^2\cdot \frac{3R}{16}}{3R^2}= \frac{1}{4}R}$

となる.

円 $N$ の反形である円 $Z$ の半径を $r_Z$ とすると,

$\begin{align} PQ^2 &=(r_Y+ r_X)^2-(r_Y-r_X)^2 \\ &= 4r_Xr_Y\\ PR^2 &= 4r_Xr_Z\\ RQ^2 &= 4r_Yr_Z \end{align}$

だから,

$PQ = PR + RQ$

より,

$\begin{align} \sqrt{r_Xr_Y} &= (\sqrt{r_X}+\sqrt{r_Y})\sqrt{r_Z} \\ \frac{1}{\sqrt{r_Z}} &= \frac{1}{\sqrt{r_X}} + \frac{1}{\sqrt{r_Y}} \end{align}$

で, これから,

$\begin{align} \sqrt{r_Z} &= \frac{1}{2 + \sqrt{3}}\sqrt{R}\\ &= (2 - \sqrt{3})\sqrt{R} \\ r_Z &= (7 - 4 \sqrt{3})R \end{align}$

となる.

この半径 $r_Z$ から, 円 $N$ の半径 $r_N$ を求めればよい.

$\begin{eqnarray} OS^2 &=& OZ^2 - r_Z^2\\ &=& ZG^2 + OG^2 - r_Z^2\\ &=& RQ^2 + OG^2 - r_Z^2\\ &=& 4r_Yr_Z + (2R+r_Z)^2-r_Z^2\\ &=& 4\{r_Yr_Z + R(R+ r_Z)\} \end{eqnarray}$

これから, 途中の計算は省略するが,

$\displaystyle{OS^2 = \frac{4(31-16\sqrt{3})}{3}R^2}$

となる. したがって,

$\begin{eqnarray} r_N &=& \frac{3\cdot 4R^2}{4(31-16\sqrt{3})R^2}(7-4\sqrt{3})R\\ &=& \frac{3(7-4\sqrt{3})}{31-16\sqrt{3}}R \\ &=& \frac{3(7-4\sqrt{3})(31+16\sqrt{3})}{193}R\\ &=& \frac{3(25-12\sqrt{3})}{193}R \end{eqnarray}$