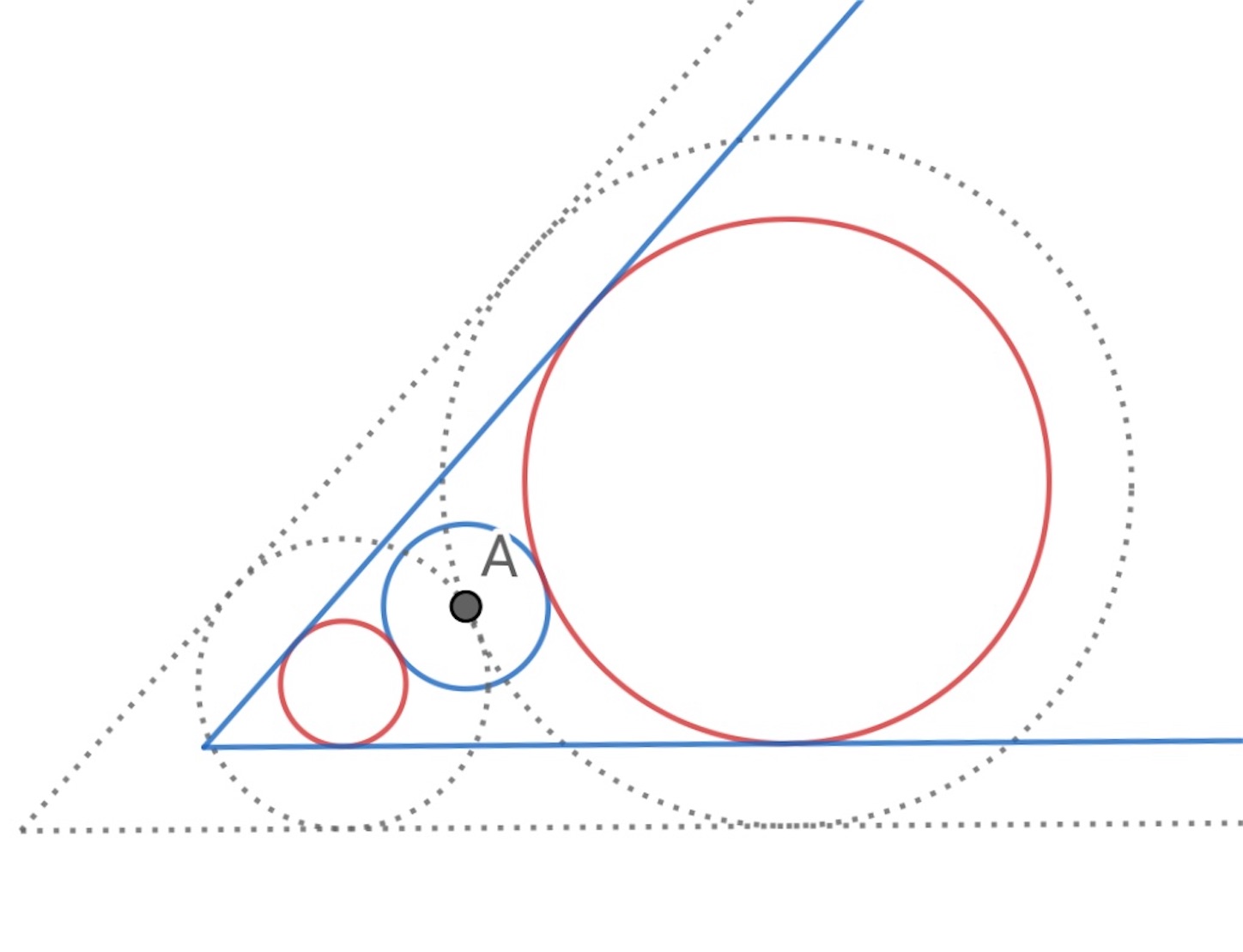
少し間があいたが, 記事 の続き.
では, 基本的な,「
点を通り
本の直線に接する円」と「
点を通り
つの円に接する円」の
つの作図の類型を見た. 与えられた同一直線にはない
点を通る円は,
点の外心を求めればよく, また与えられた
直線が
点で交わらず, どの
本も平行でない場合には, 三角形の内接円または傍接円を描けばよい.「点」「直線」「円」の語の重複組合せは全部で
(通り) なので, 残る
通りについて簡単に見ておくことにする.
まず,「 点を通り
つの円と
本の直線に接する円」を考える.
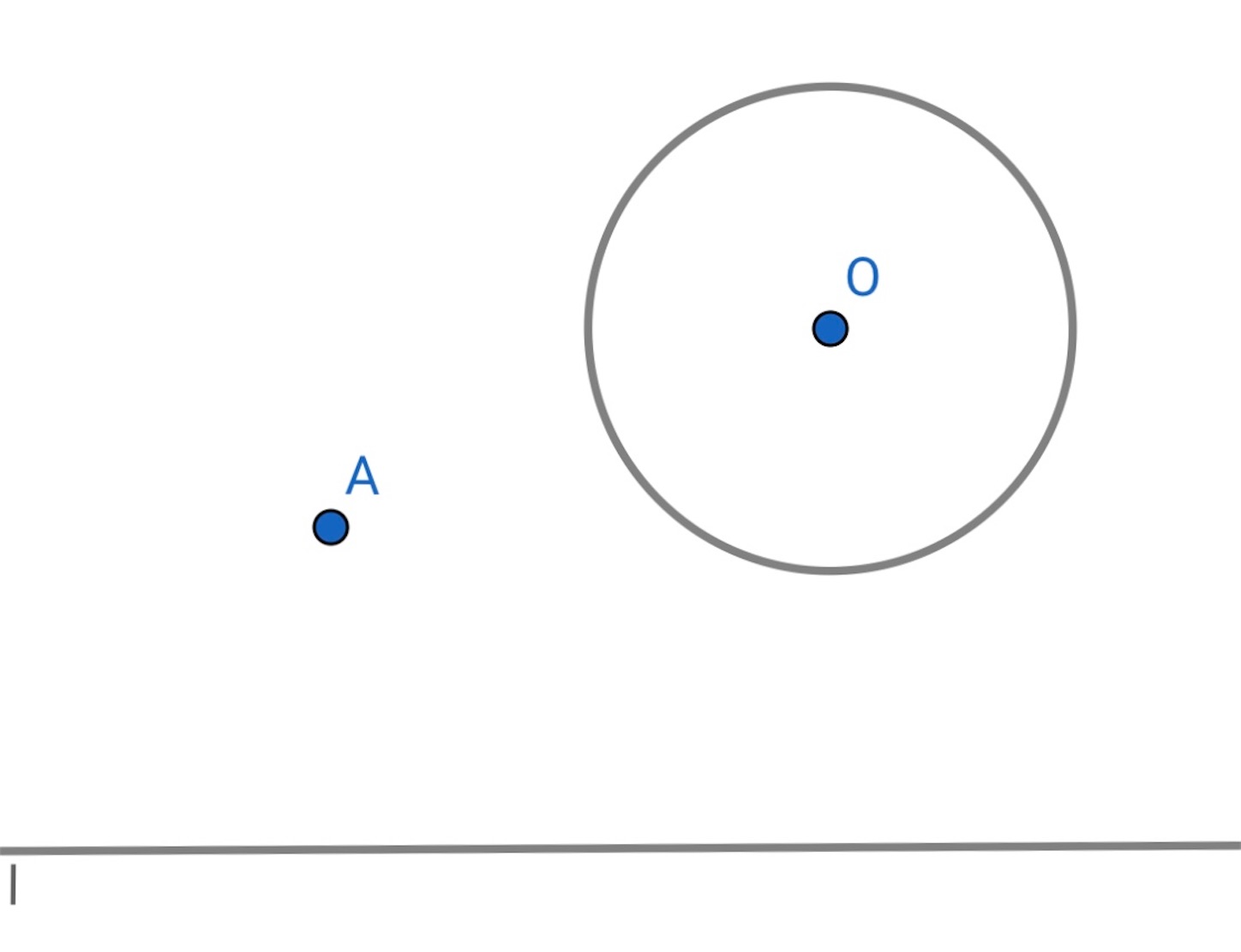
円 の中心をとり直線
に垂線を下ろす.
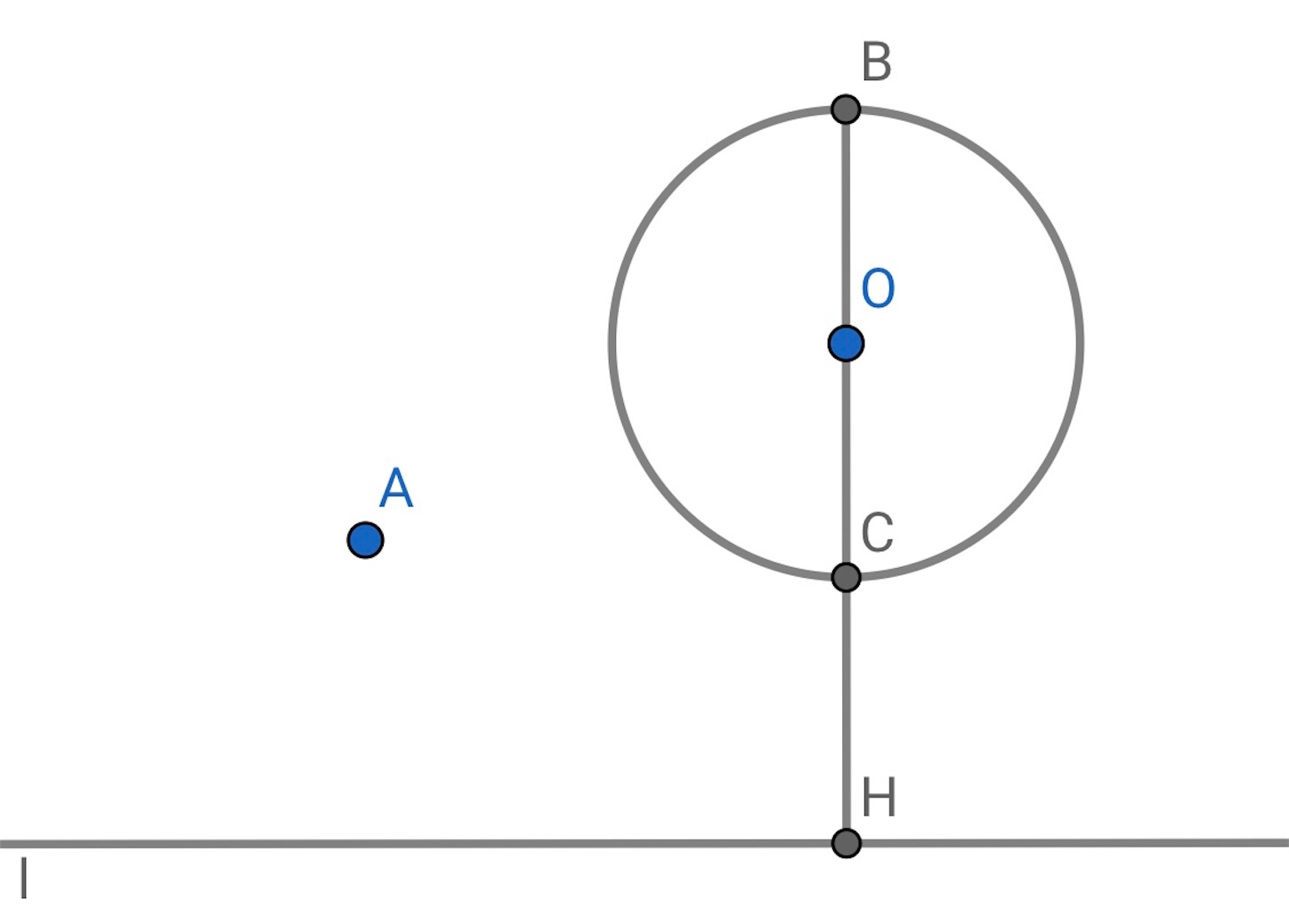
点
,
,
を通る円を描き,
とその円の交点を
とする (
が
で円と接する場合は, 作図は容易にできる).
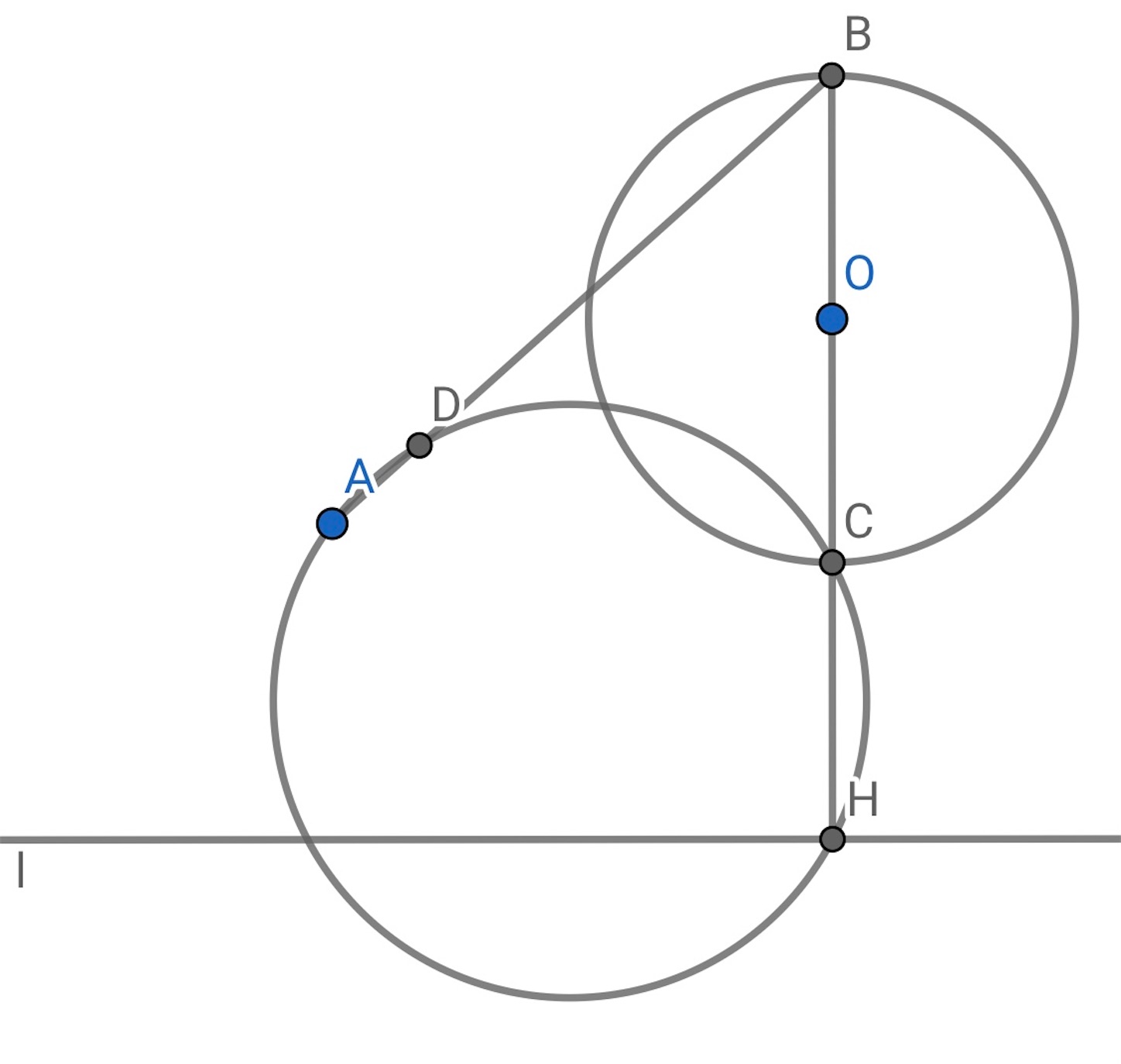
後は前の記事でやった 点
,
を通り直線
に接する作図か,
点
,
を通り円
に接する作図のどちらかを行えばよい.
と
を入れ替えても同じような作図が可能なので, 一般には
つの円が作図できる.
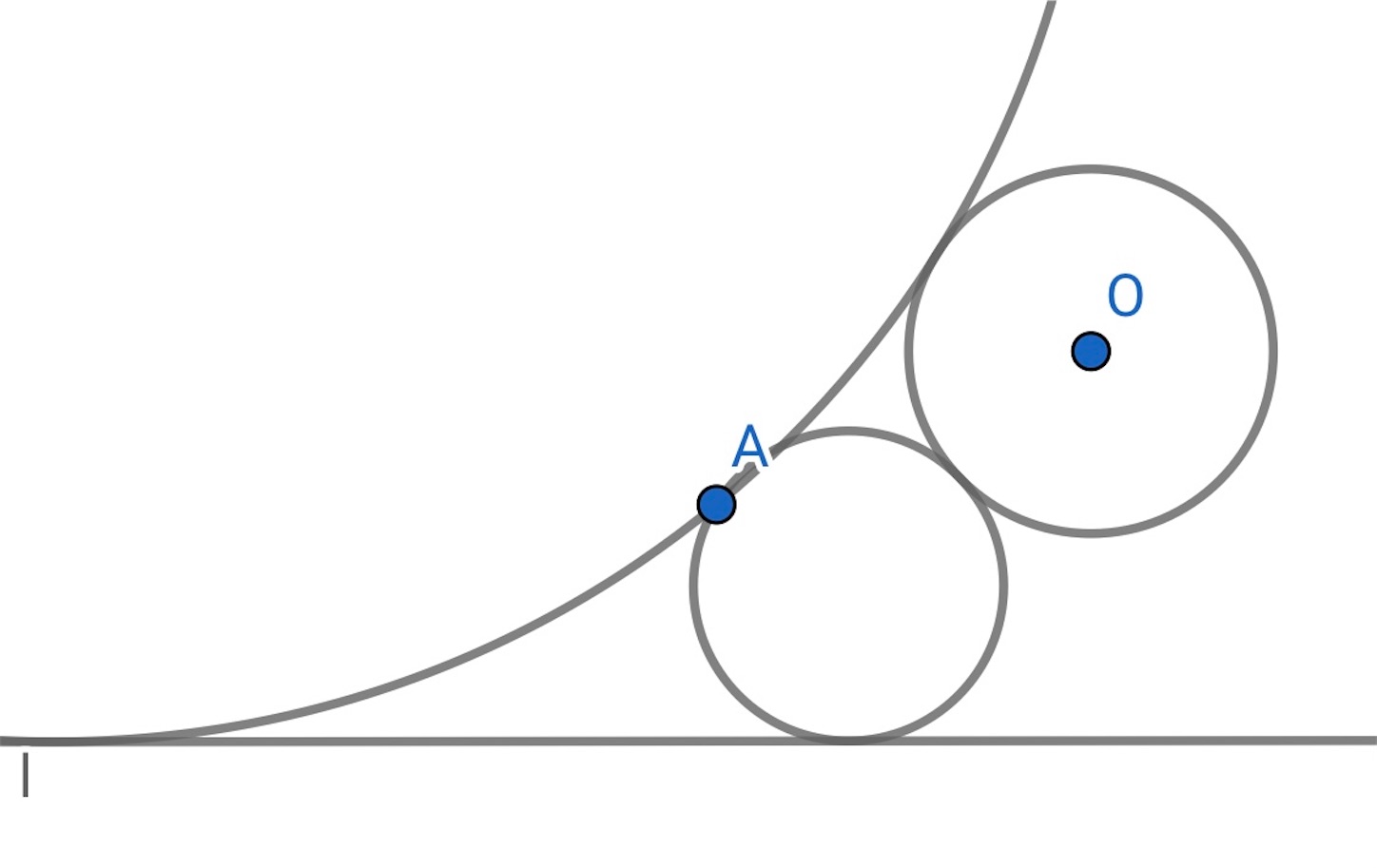
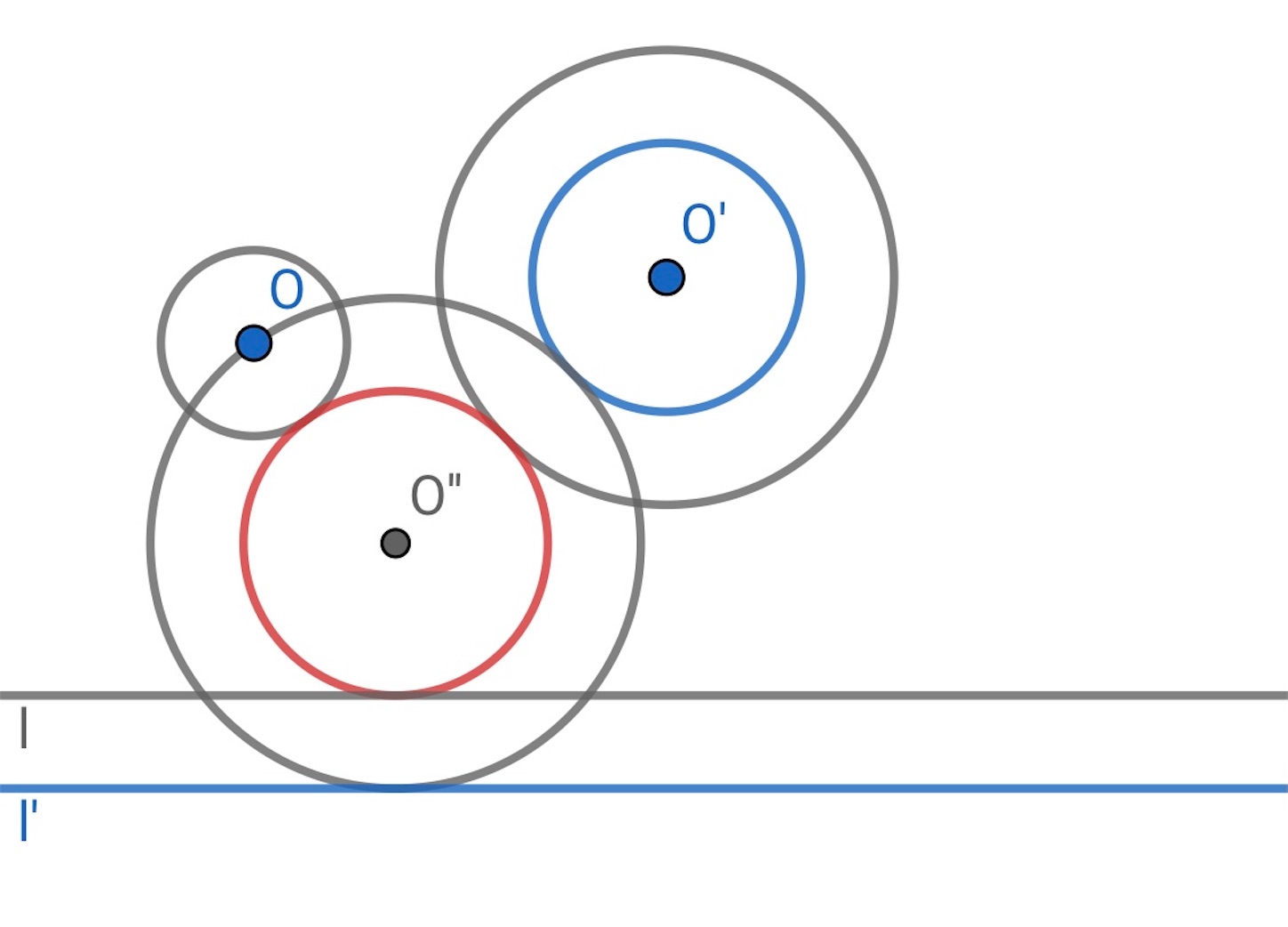
次に,「 つの円と
本の直線に接する円」を考える.
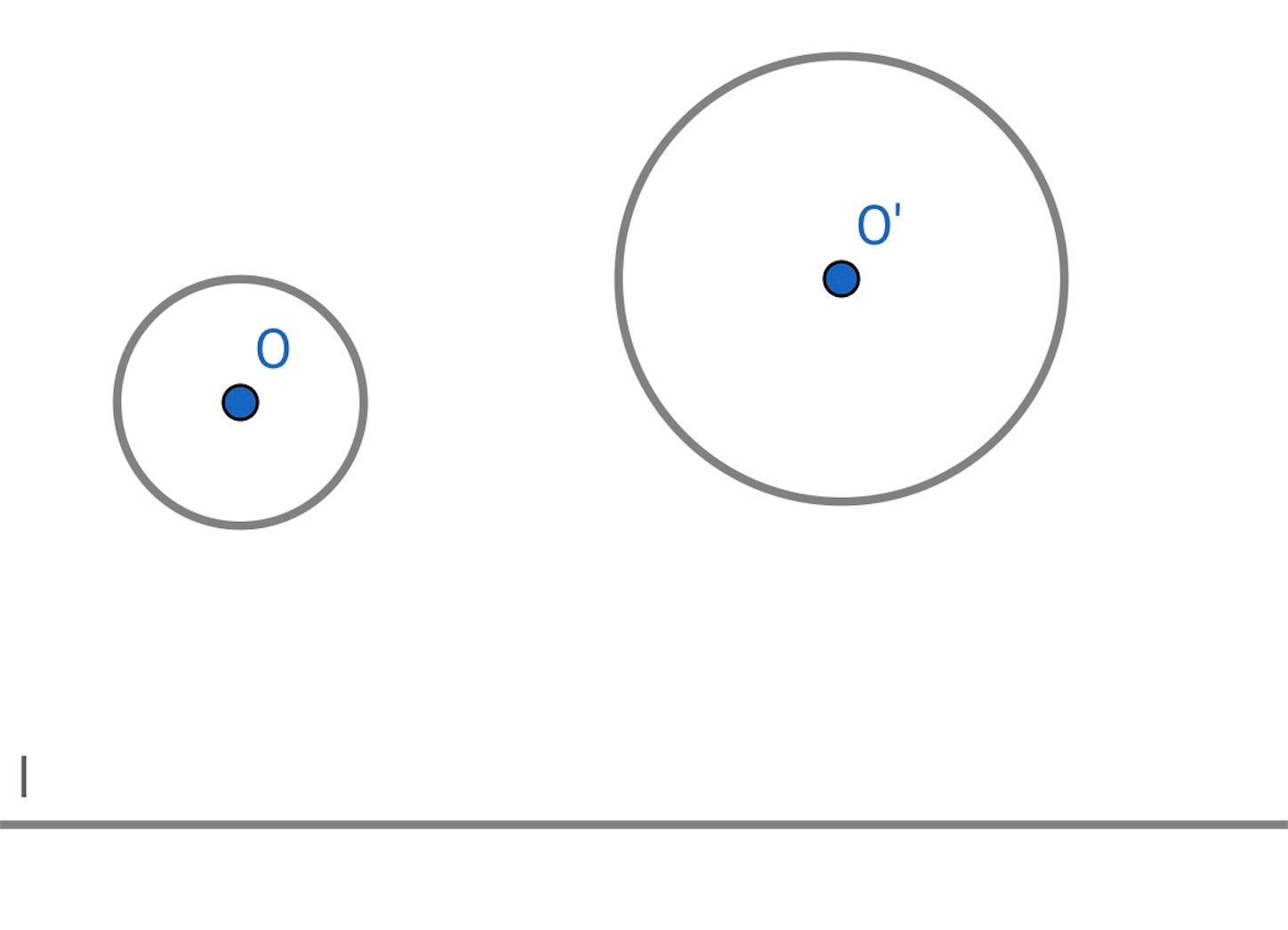
小さい方の円 の半径を
とし, 円
,
の半径を
だけ縮める. そうすると円
は点になる. 直線
を平行に
だけ遠ざけた直線を
とする.
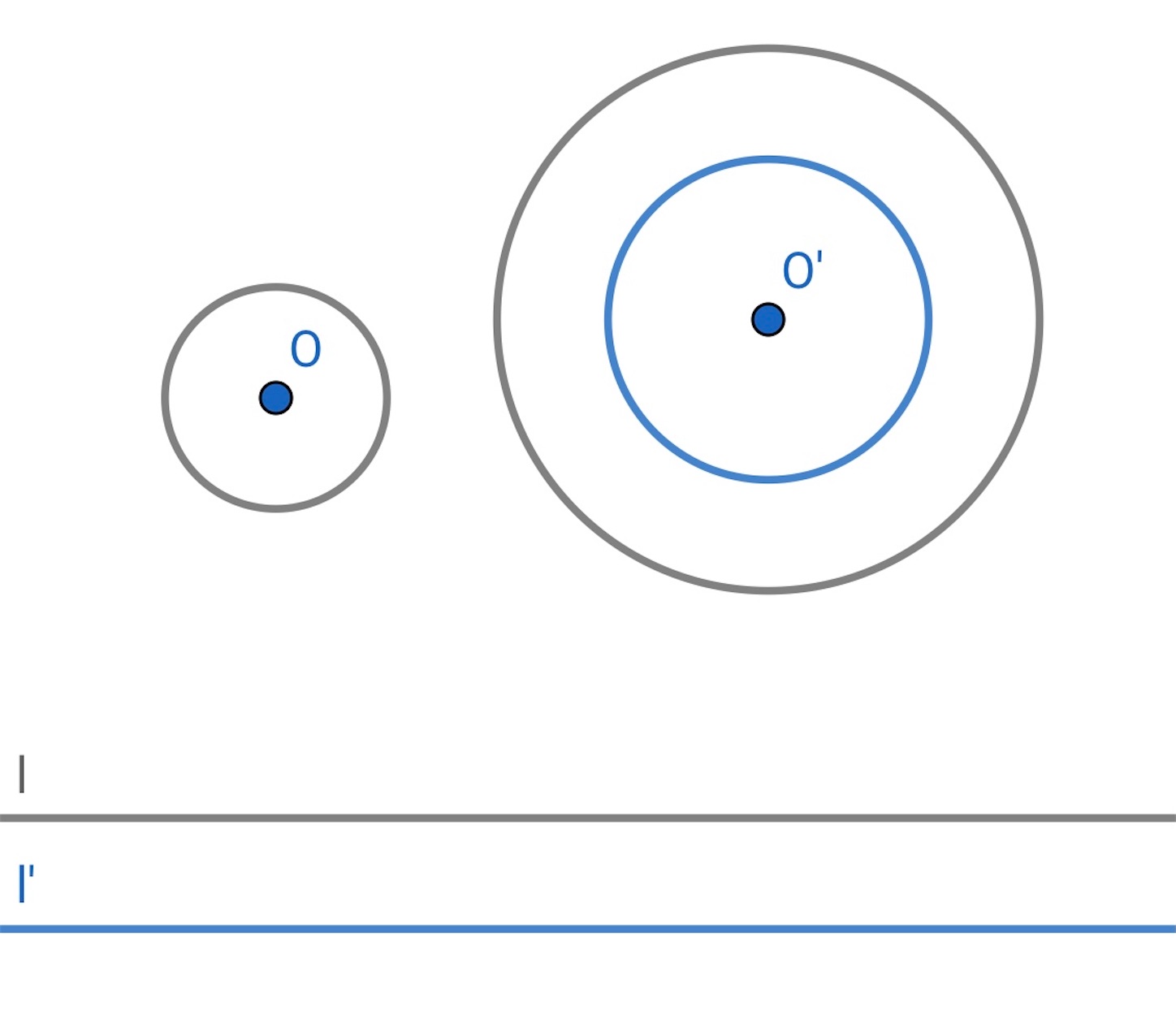
先程と同じ手順で, 点 を通り, 半径を縮めた円
と直線
に接する円を描く.
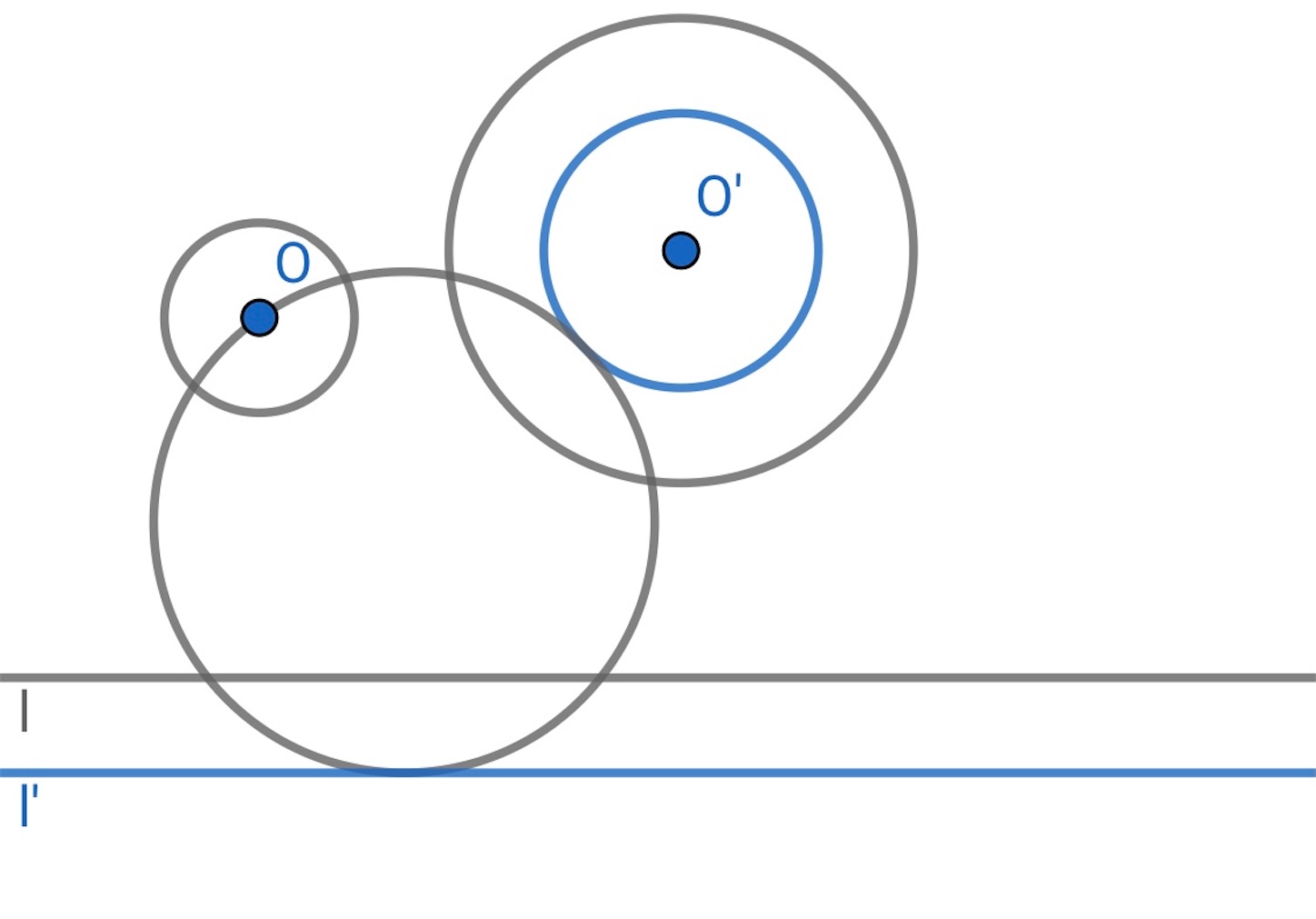
できた円の中心を求めて, 半径 だけ縮めると目的の円が得られる. 下図は
つの円しか描いていないが, 一般にはこのような円は
つできるはずである.
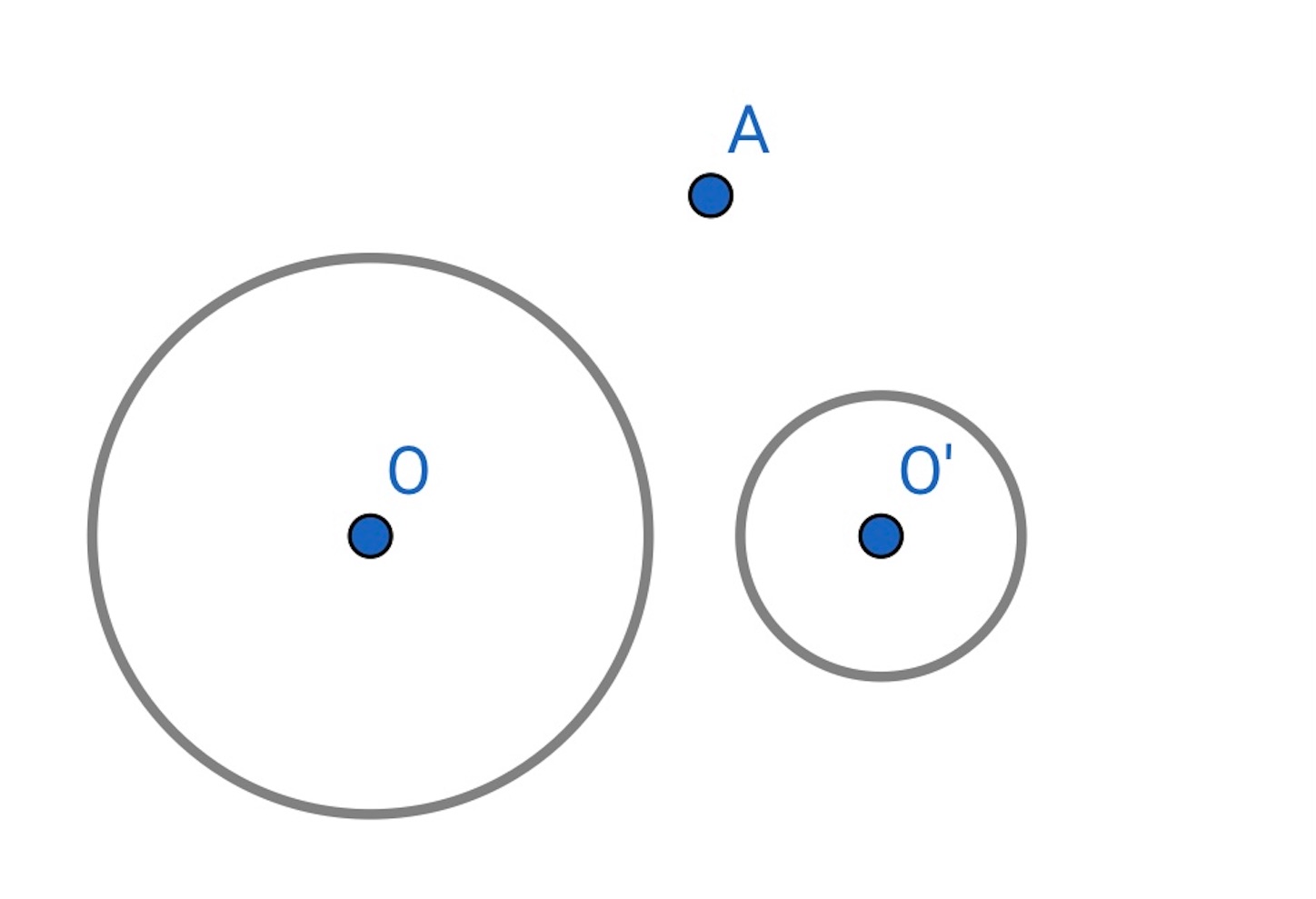
次は, 与えられた 点を通り, 与えられた
円に接する円を描く.
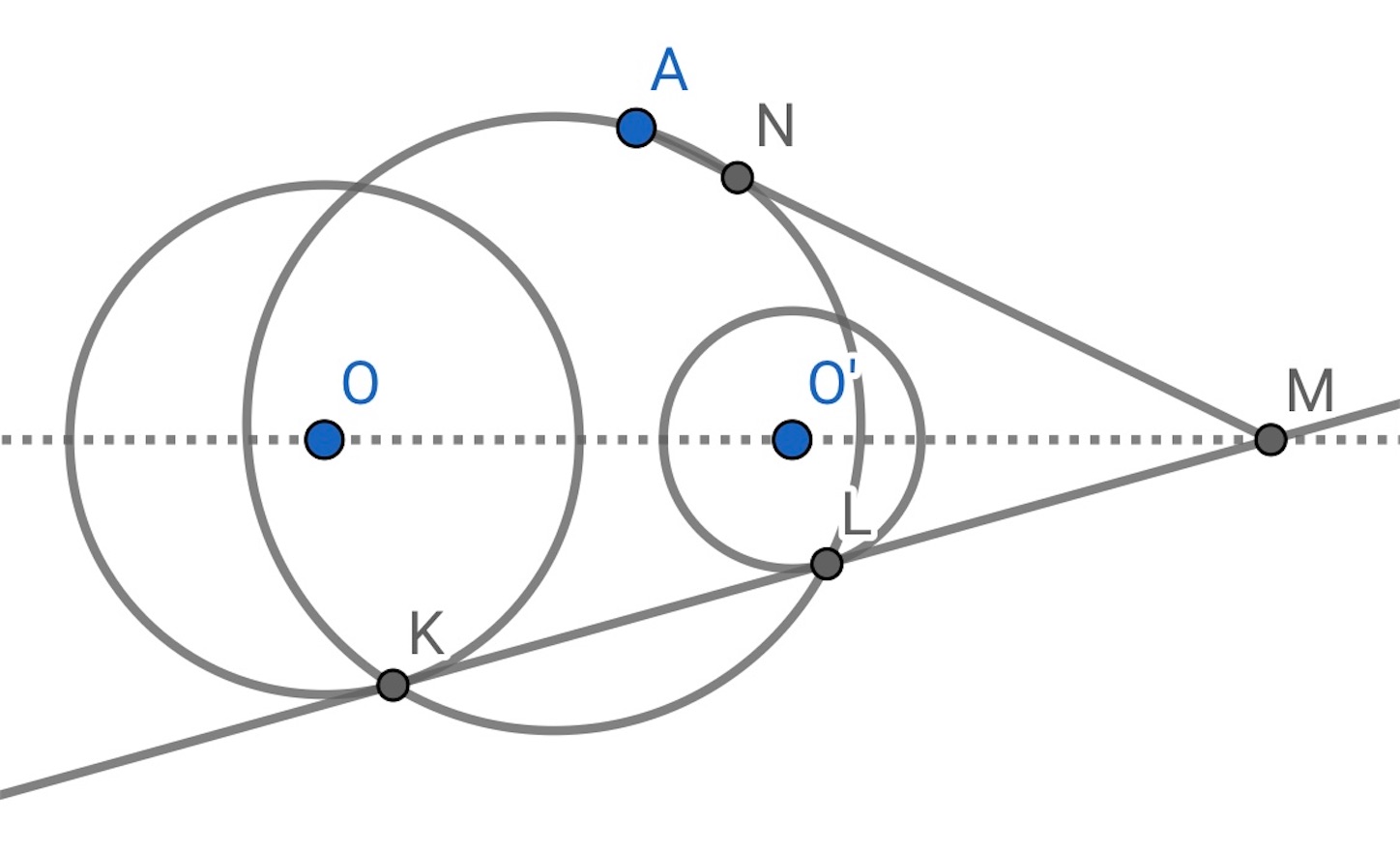
円 と
の共通接線を引き,
つの円の中心を通る直線との交点を
(相似の中心) とする. 接点
,
と
を通る円を描き, 直線
とその円の交点を
とする.
後は前回の記事の手順で, 点
,
を通り円
と接するように作図すれば, 目的の円が得られる.
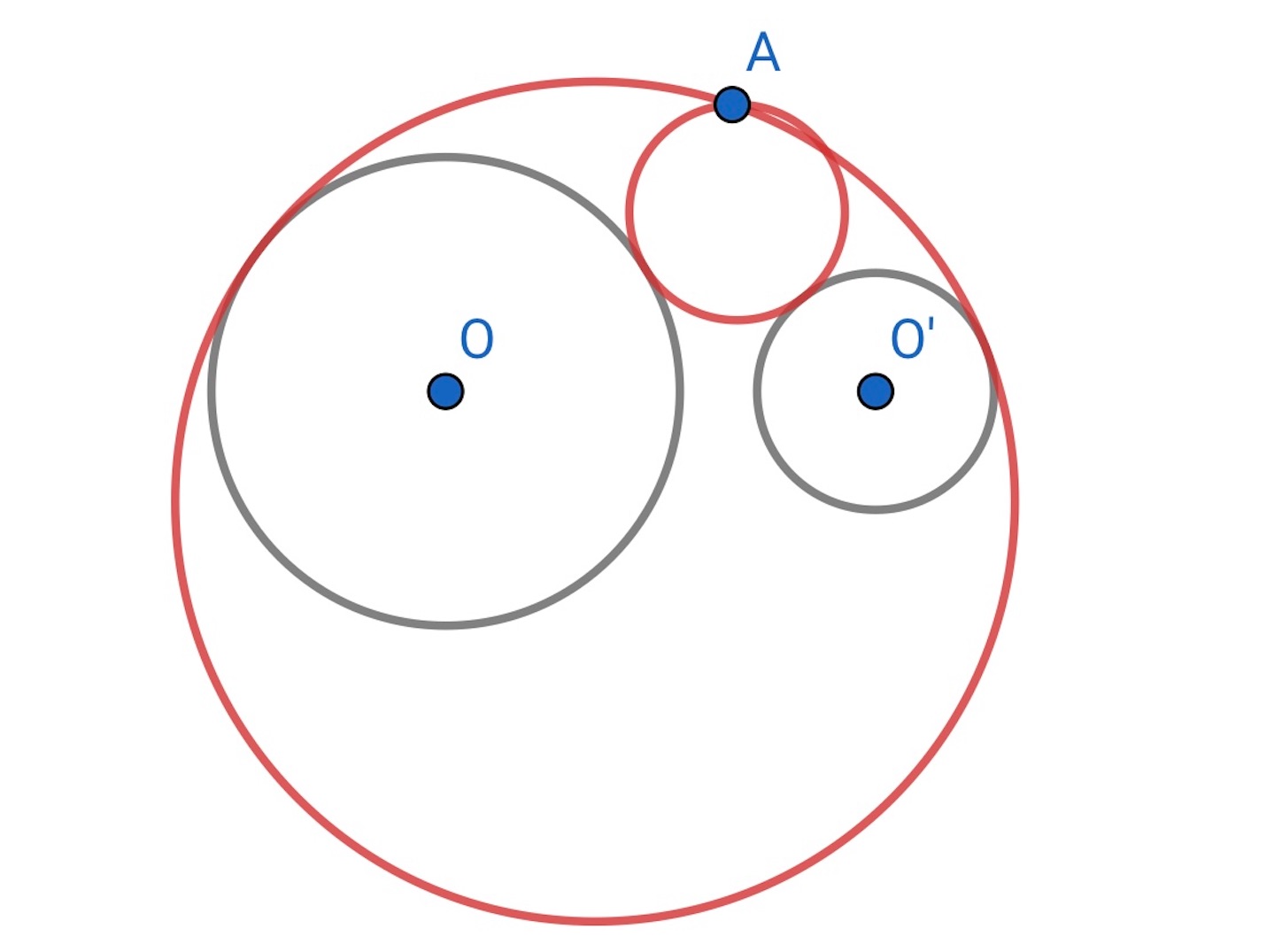
つの定円のもう一つの相似の中心を考えれば, 一般にこのような円は
つ書けるはずである.
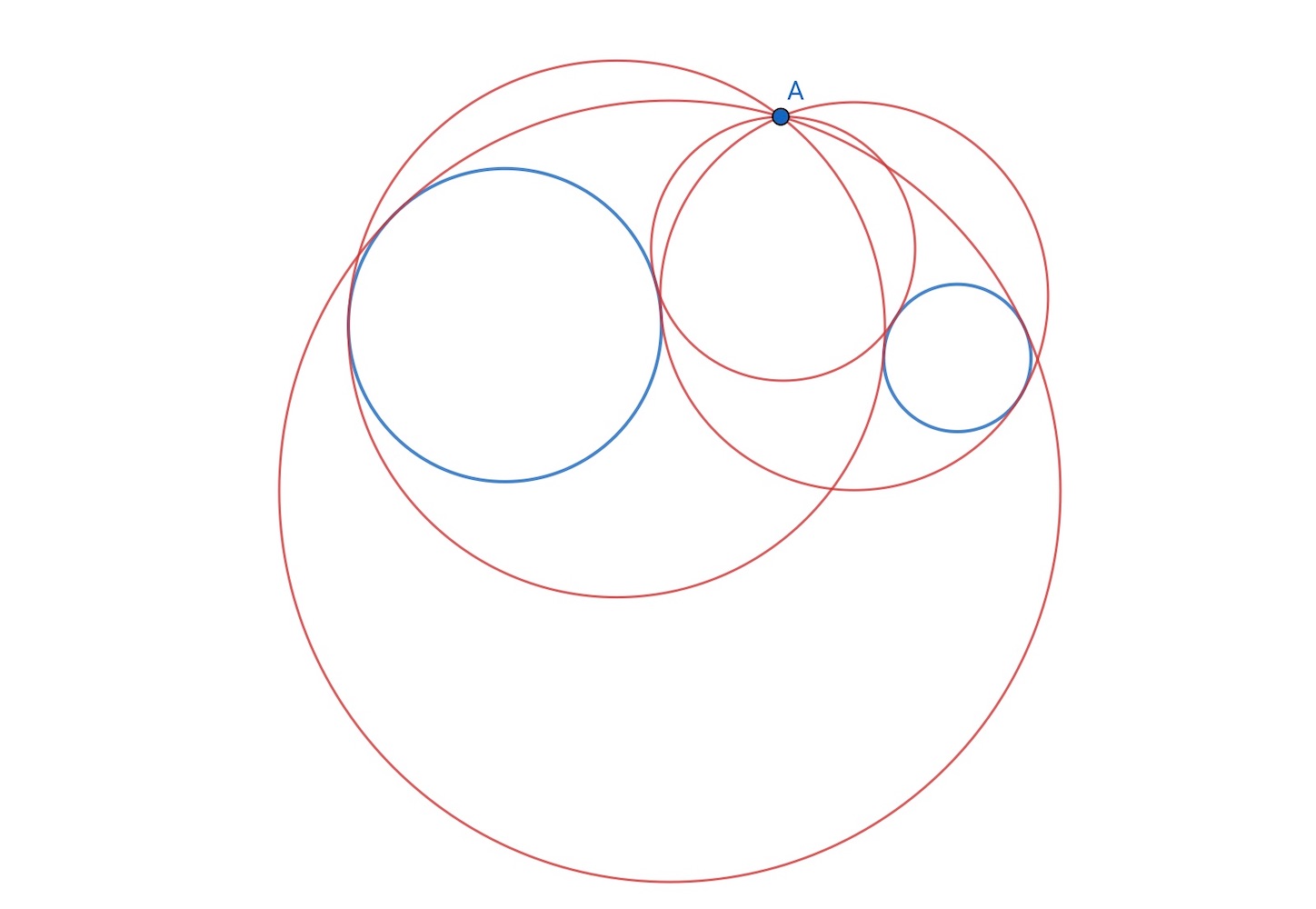
次は, つの円に接する円だが, これはもう察しがつくと思うので, 説明は省略する.
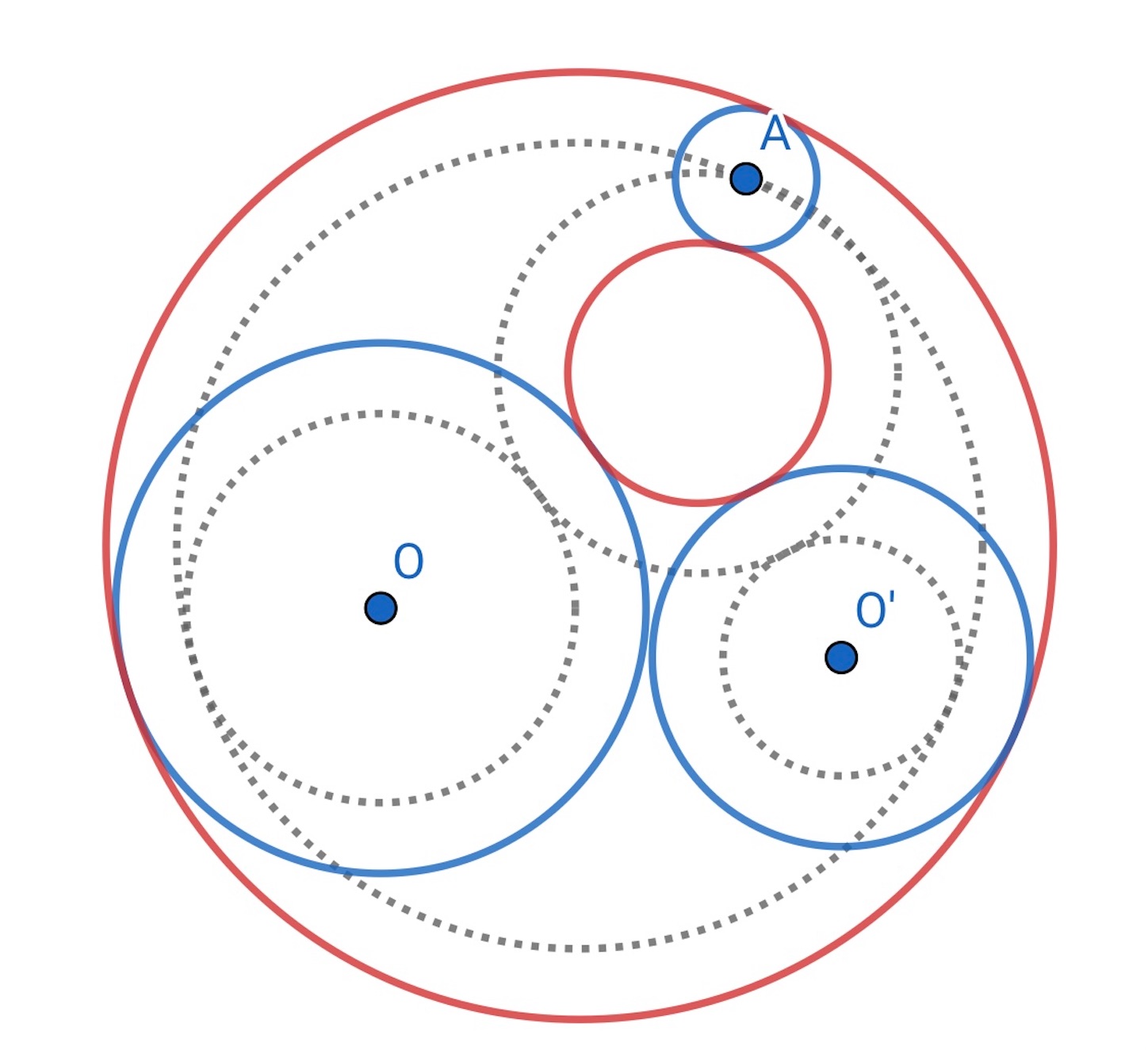
最後に, 与えられた点 を通り,
直線と接する円は,
直線に接する適当な円
を書いて, 以下のように作図すればよい.
と
は平行,
と
も平行である.
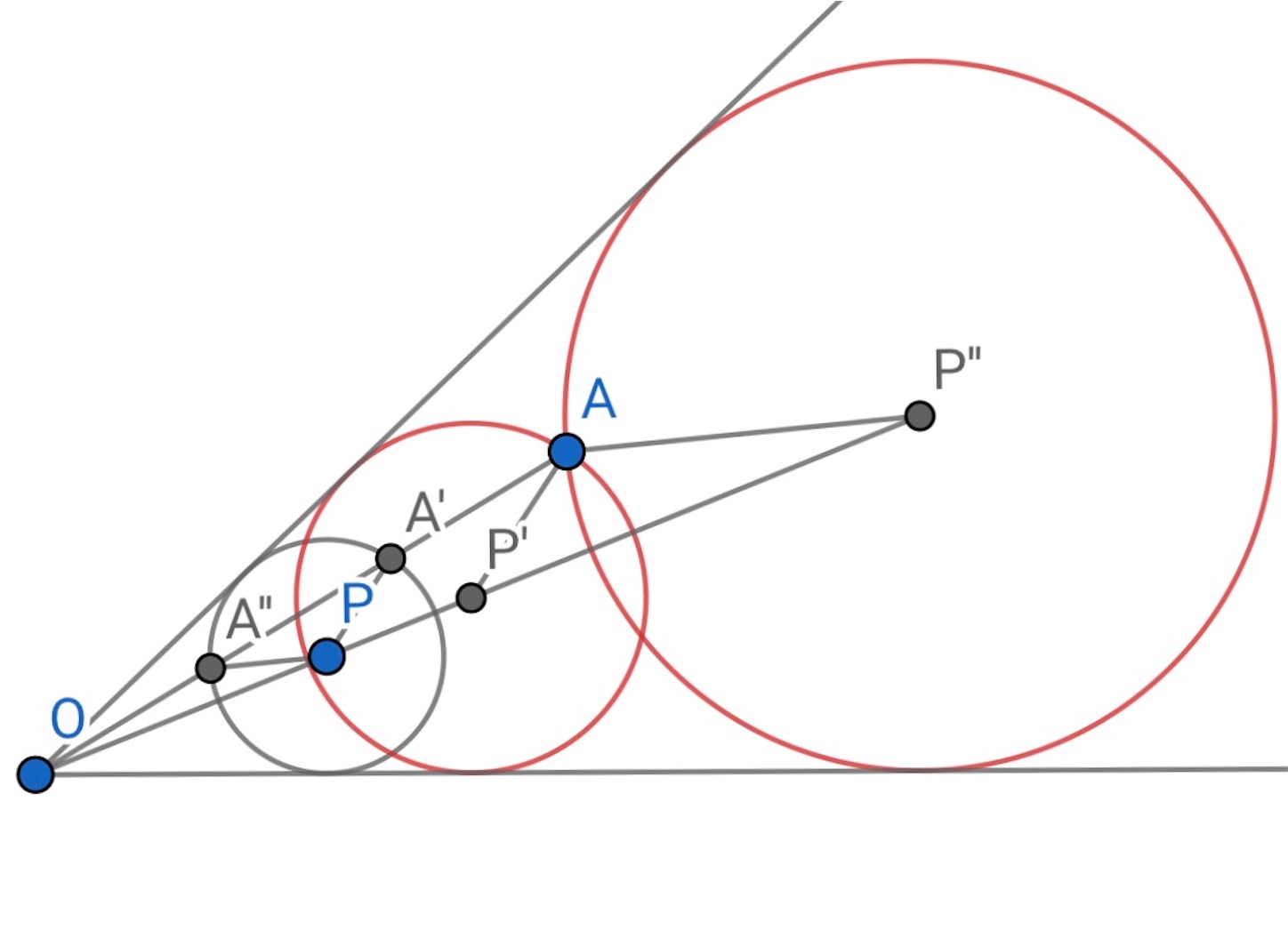
これが, 作図できれば, 直線と円に接する円も描けることがわかる.