陥没地帯 (200) - ノリの悪い日記

ある人が学ぶことが, どんどん貧しくなっている下のような具体例を挙げてくれていて, なるほどなと思った.

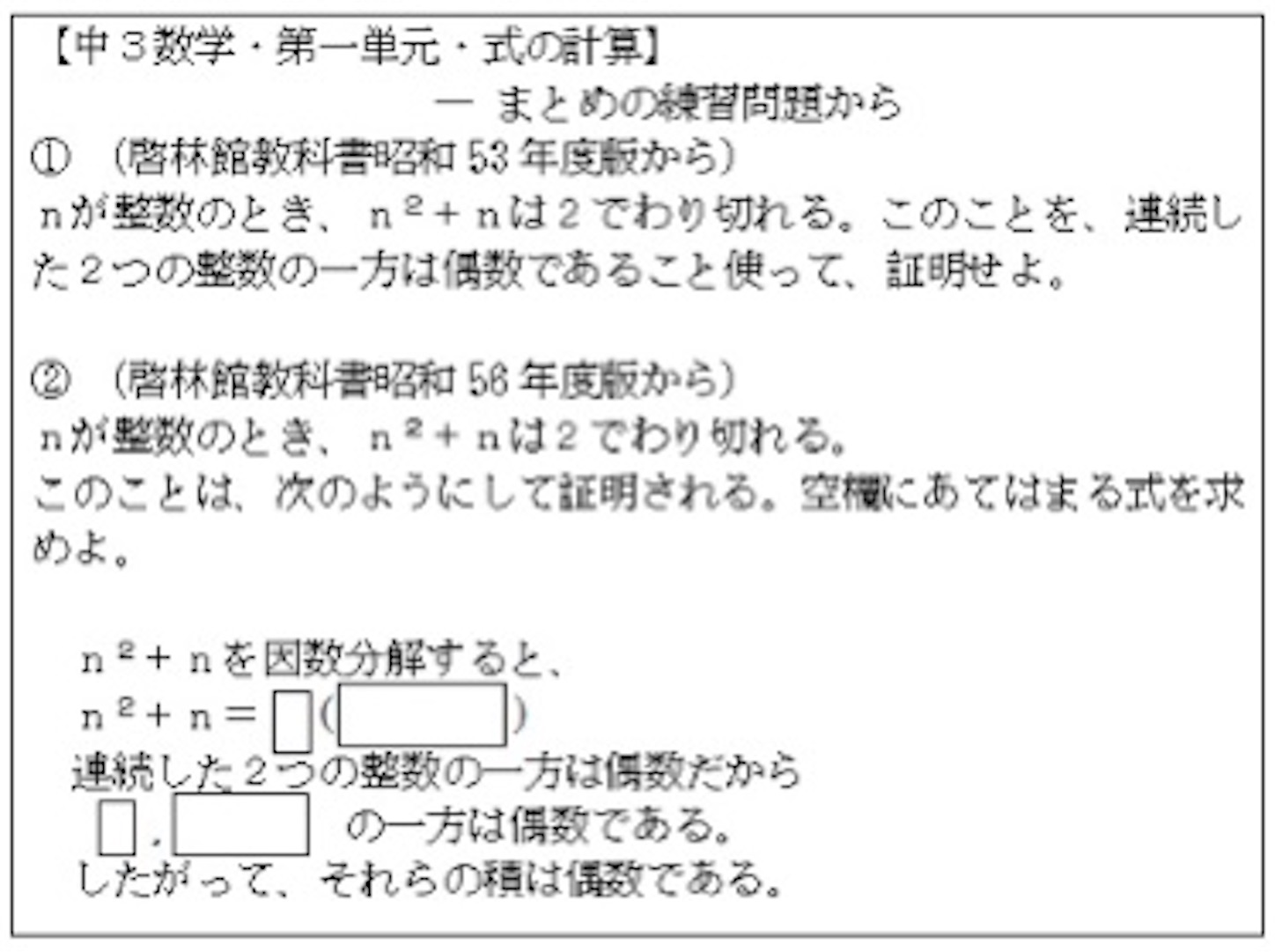
その人は, 自分だったら「連続した $2$ つの偶数の積は, $8$ の倍数であることを証明せよ」とノーヒントで出すとも言っているが, この発言にも共感できる. 自分もかつて同じ問題を考えて, そのときに連続した二つの整数の一方が必ず偶数であることが, とてつもなく偉大な事実のように思え, それ以来整数の問題を解くときにはその事実が自然に頭に浮かんで利用できるようになったからである. 側から見れば大変ささやかといえるだろうが, その小さな発見が数学をやる喜びのひとつであろう. それを最初から消し去るなんて……

昭和 $53$ 年というと「数学の現代化」が喧しくいわれた最後くらいで, 昭和 $56$ 年は「ゆとり教育」が始まった年だが, そんなレッテルとは関係なく昭和 $53$ 年の時点ですでに「学ぶとは (小さくはあっても) 強度の体験である」ことがひたすら忘れさられ, それがさらに加速して現代に至っていると思わせてしまうような例である. 最近, 昭和初期の数学学習誌を熟読して, その時代の幾何がいかに面白かったか *1 を実感して, ファンになってしまった自分としては, このことは, 旧制中学の出題の仕方にまで遡って比較してみると事態がもっと明らかになるように感じてしまう. (まあ, 世界的な大衆化現象のひとつと言ってしまえば, それまでだが.)

その一方で, $1991$ 年の東京大学の入試問題のような良問は出題されている.

【問】
$xy$ 平面上, $x$ 座標, $y$ 座標がともに整数であるような点 $(m, n)$ を格子点と呼ぶ. 各格子点を中心として半径 $r$ の円がえがかれており, 傾き $2/5$ の任意の直線は, これらの円のどれかと共有点をもつという. このような性質をもつ実数 $r$ の最小値を求めよ.

【解】
任意の格子点を選んで, それを原点 $(0, 0)$ とする. 右を $x$ 軸方向, 上を $y$ 軸方向とする. まず, その原点を通る傾き $2/5$ の直線を考える. $x$ 軸方向に $5$ 進むと, 直線は格子点 $(5, 2)$ を通るが, $2$ と $5$ は素だから $(0, 0)$ と $(5, 2)$ の間で直線が格子点を通ることはない.

原点を通過する傾き $2/5$ の直線を道だと考えて, その道沿いに右へ進んでいくとする. 原点ですぐ上と下の格子点の $y$ 軸方向の相対変位は, 上 $1$ , 下 $1$ である. $x = 1$ まで直線に沿って進むと, すぐ上の格子点の変位は、 $3/5$ , 下は $2/5$ である。同じようにして, $x = 2$ のとき, 上に $1/5$ , 下に $4/5$ , $x = 3$ のとき, 上に $4/5$ , 下に $1/5$ である. $x = 4$ では上に $2/5$ , 下に $3/5$ となる.

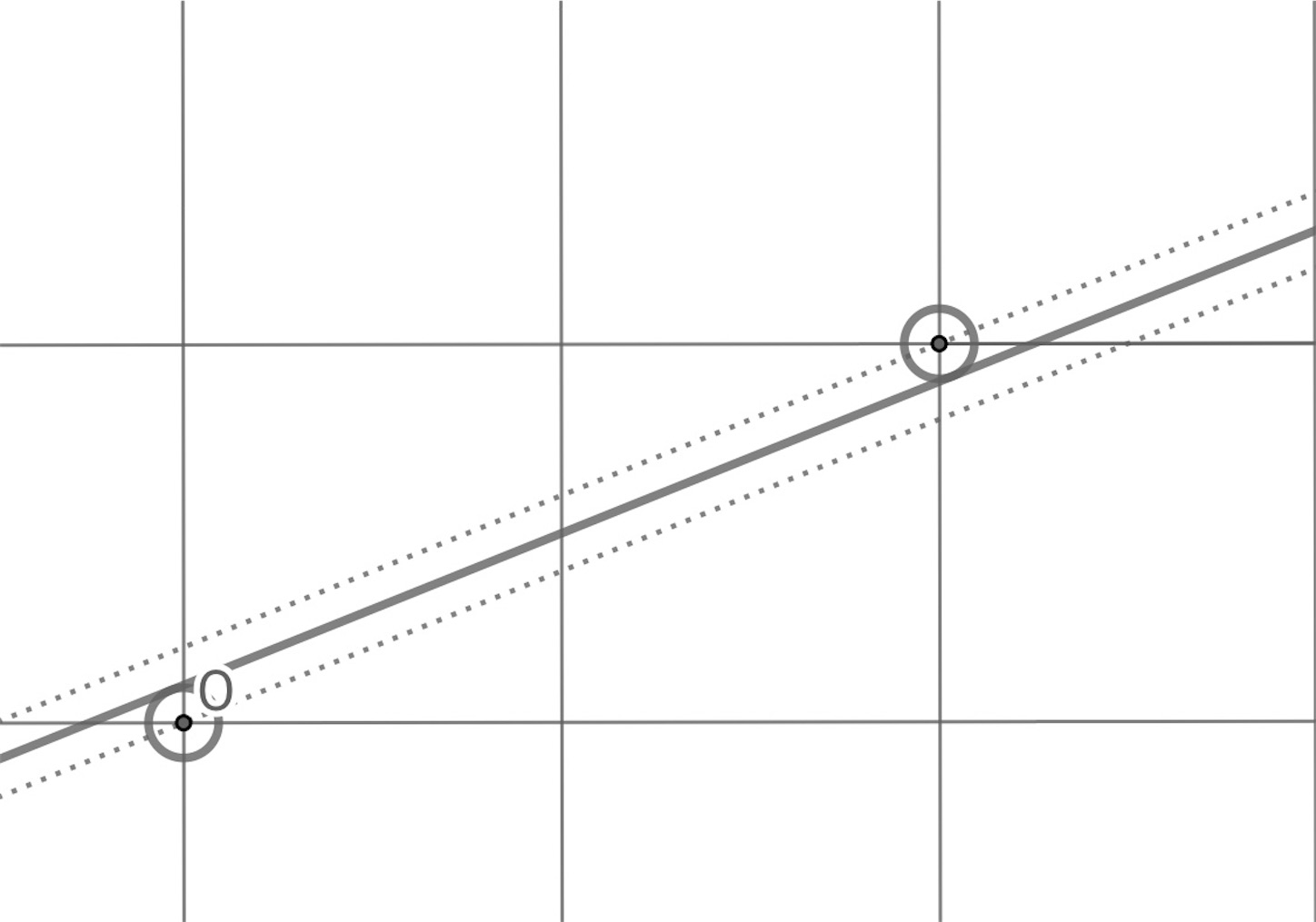
今度は, 原点を通る傾き $2/5$ の直線を少しずつ $y$ 軸方向 (上) に移動させていく. そうすると, 最初に $(2,1)$ の場所の格子点を通過することがわかる. そこで, $(2,1)$ を新しい原点とすれば, 対称性から後は同じことの繰り返しである. 同じようにして, 直線を下に移動させれば, 最初に通過する格子点は, $(3,1)$ であり, $(3,1)$ (または $(-2,-1)$ )に移動すれば, 後は同じことの繰り返しである.

そうすると, 原点を通過した直線を連続的に上下に移動させて, 次の格子点を通るまでの間に, 常に原点と $(2,1)$ または $(3,1)$ の格子点の円と共有点をもっていれば題意を満たすことから, $r$ の最小値は上の図に示したように、移動のちょうど中間点で, 直線が $2$ つの円の共通接線となる場合であることがわかる.

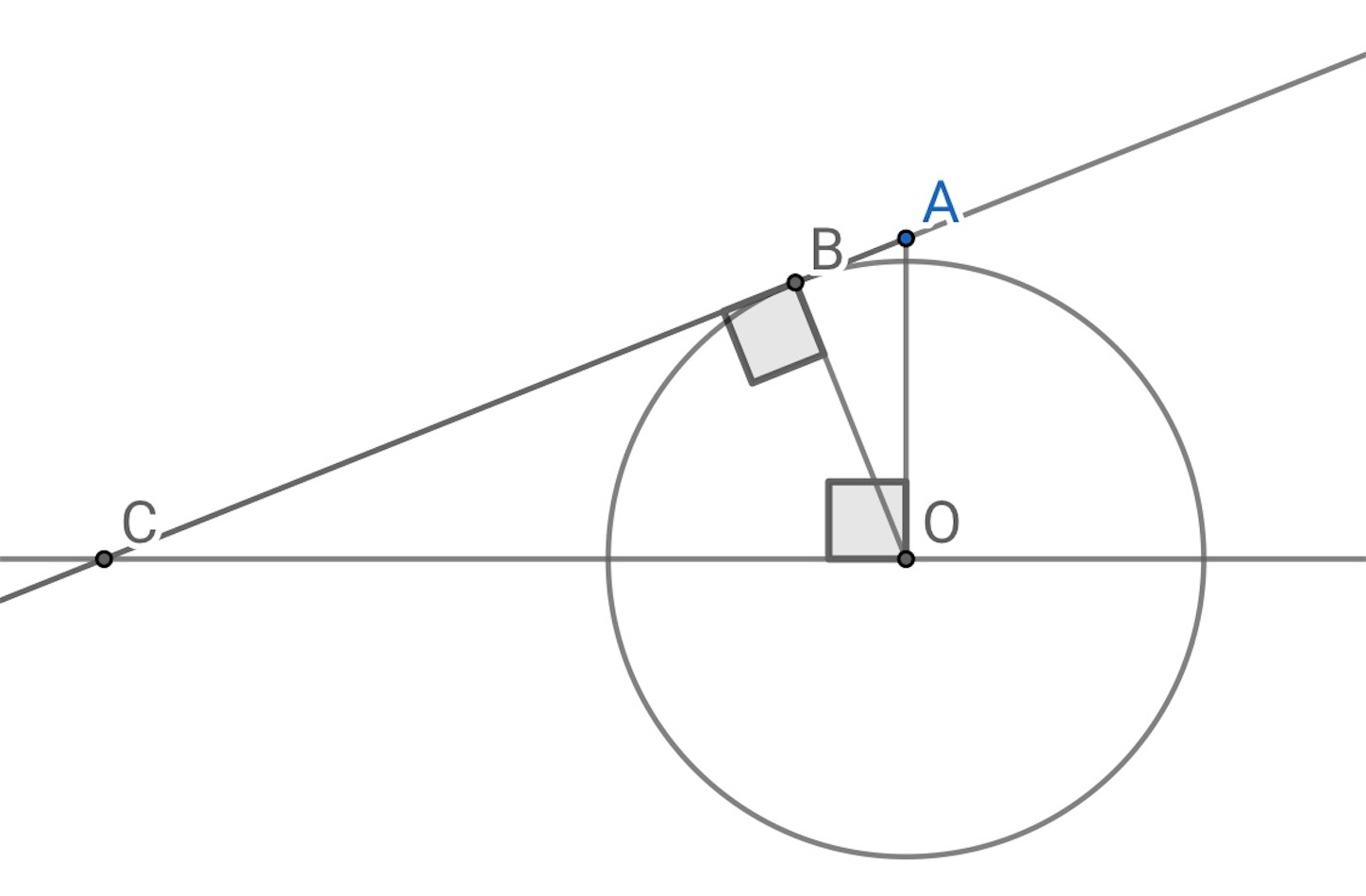
具体的な円の半径の最小値 $r$ の計算は, 上の図の $\triangle OAB$ にピタゴラスの定理を適用して,

$\displaystyle{ OA = \frac{1}{5} \times \frac{1}{2}}$

であることから,

$\begin{align} r^2 + \left(\frac{2r}{5}\right)^2 &= \left(\frac{1}{10}\right)^2\\ \left(\frac{29}{25}\right)r^2 &= \left(\frac{1}{10}\right)^2 \end{align}$

$r > 0$ より,

$\displaystyle{r = \frac{1}{2\sqrt{29}}= \frac{\sqrt{29}}{58}}$
//

【別解】
上記の解はやや冗長なので, より解析的な解を与えておく. ここでは, 以下の事実を使う.

任意の実数 $x$ に対して整数 $n$ を適当にとって $|x-n| \leq r$ となることと, $\displaystyle{\frac{1}{2} \leq r}$ であることは同値である.

傾き $2/5$ の任意の直線を

$2x - 5y + k = 0$

とおく. $k$ は任意の実数である.

任意の傾き $2/5$ の直線に対して, 適当にとった格子点 $(m, n)$ を中心とする半径 $r$ の円が共有点をもつ条件は, 点と直線の距離の公式より,

$\displaystyle{\frac{|2m-5n + k|}{\sqrt{29}} \leq r}$

で与えられる. $m$ , $n$ は任意の整数であり, また $2$ と $3$ は互いに素であるから, 1次不定方程式の整数解の存在条件により, $-N = 2m-5n$ とおくと, $N$ は任意の整数である. したがって, 傾き $2/5$ の任意の直線に対して円が共有点をもつ格子点が存在する条件は,