前回の 年度の神奈川県公立高校入試問題の続き.
【問】
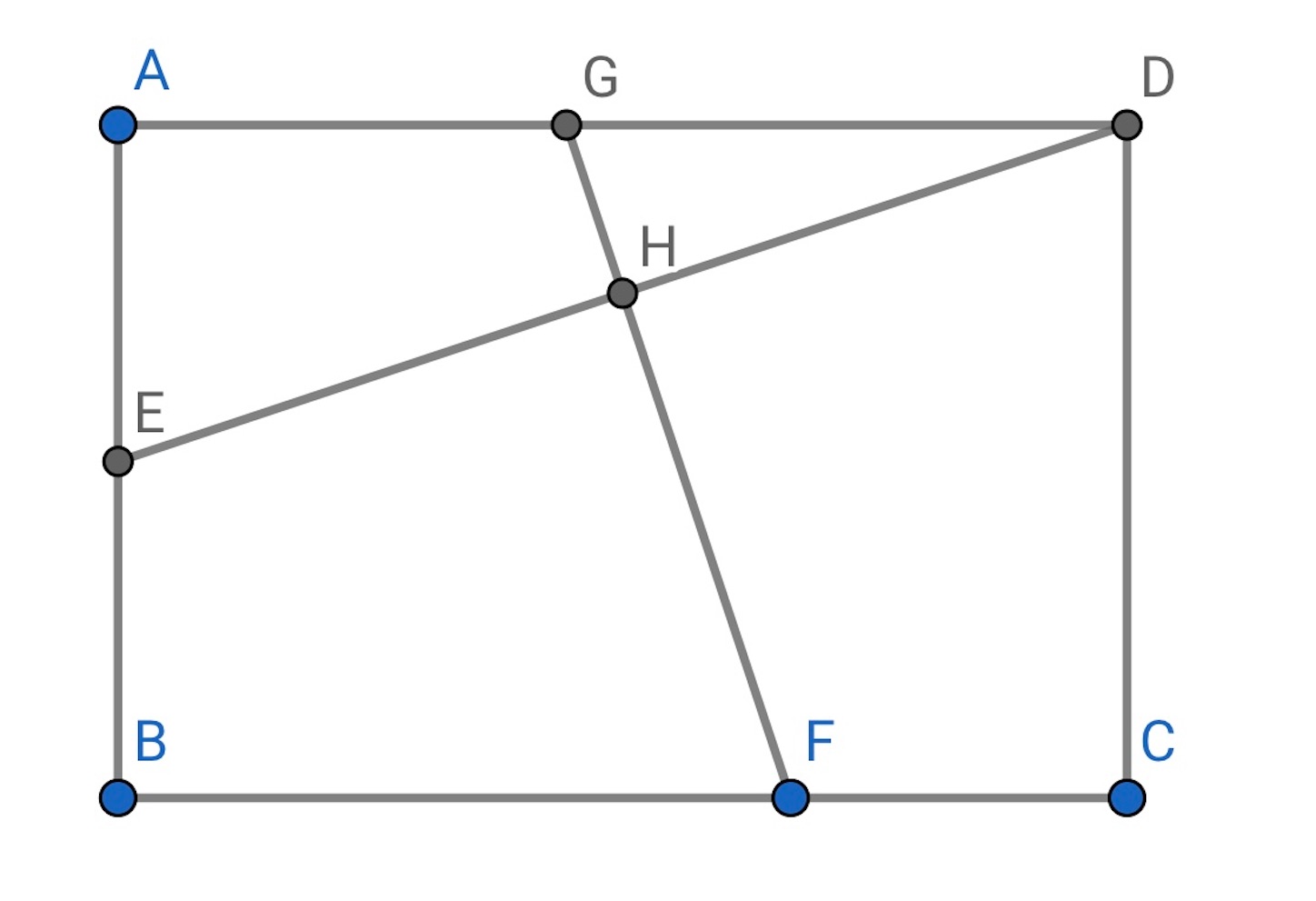
図のように長方形 があり, 辺
の中点を
とする. また辺
上に点
を
となるようにとり, 辺
上に
を線分
と線分
が垂直に交わるようにとる. さらに線分
と線分
の交点を
とする.
,
のとき, 線分
の長さを求めなさい.
※ 前回は別解として, 下図のように、 は
の重心であることを示したところで寝てしまった.
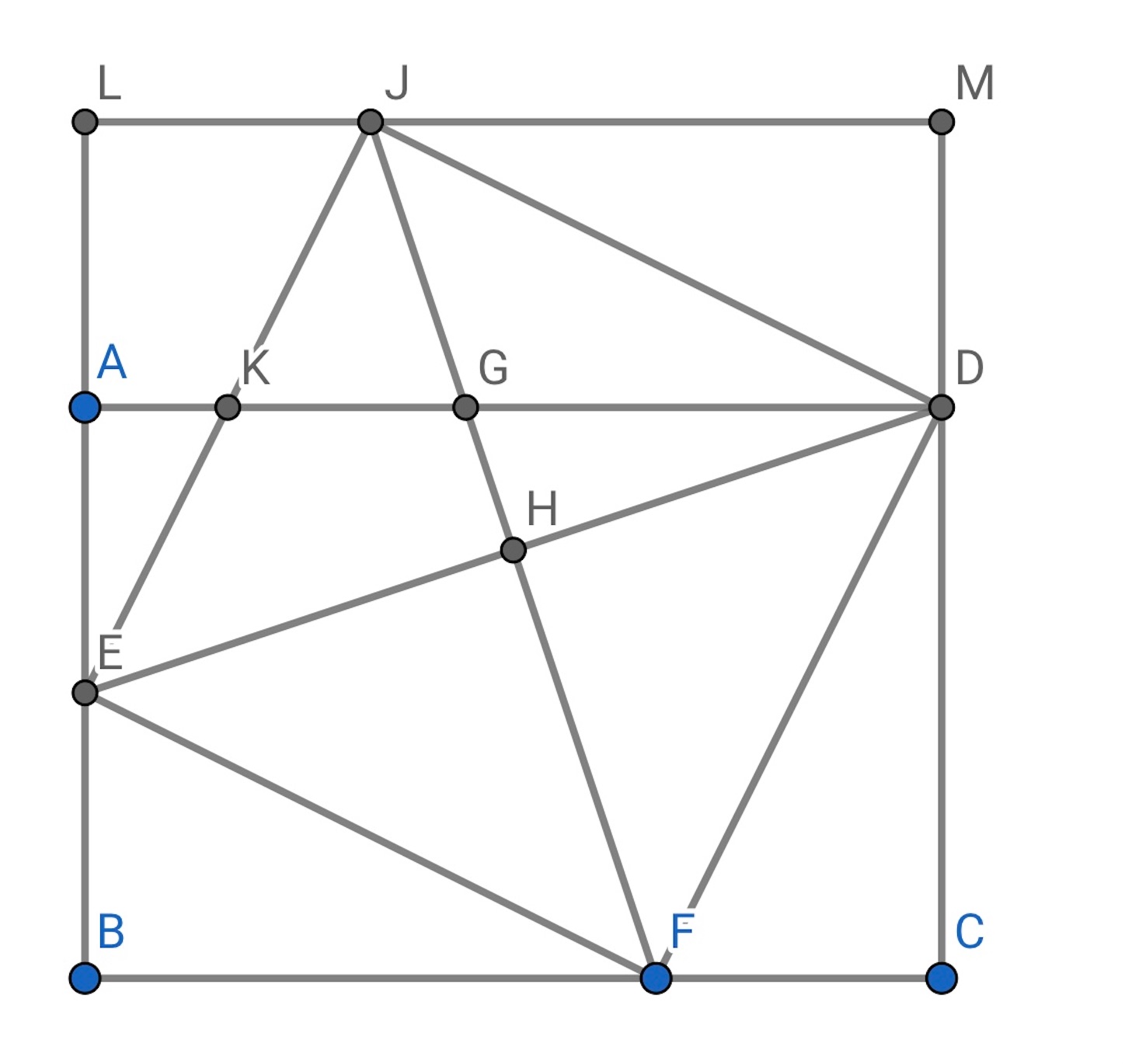
他にないか考えてみる.
【別解 】
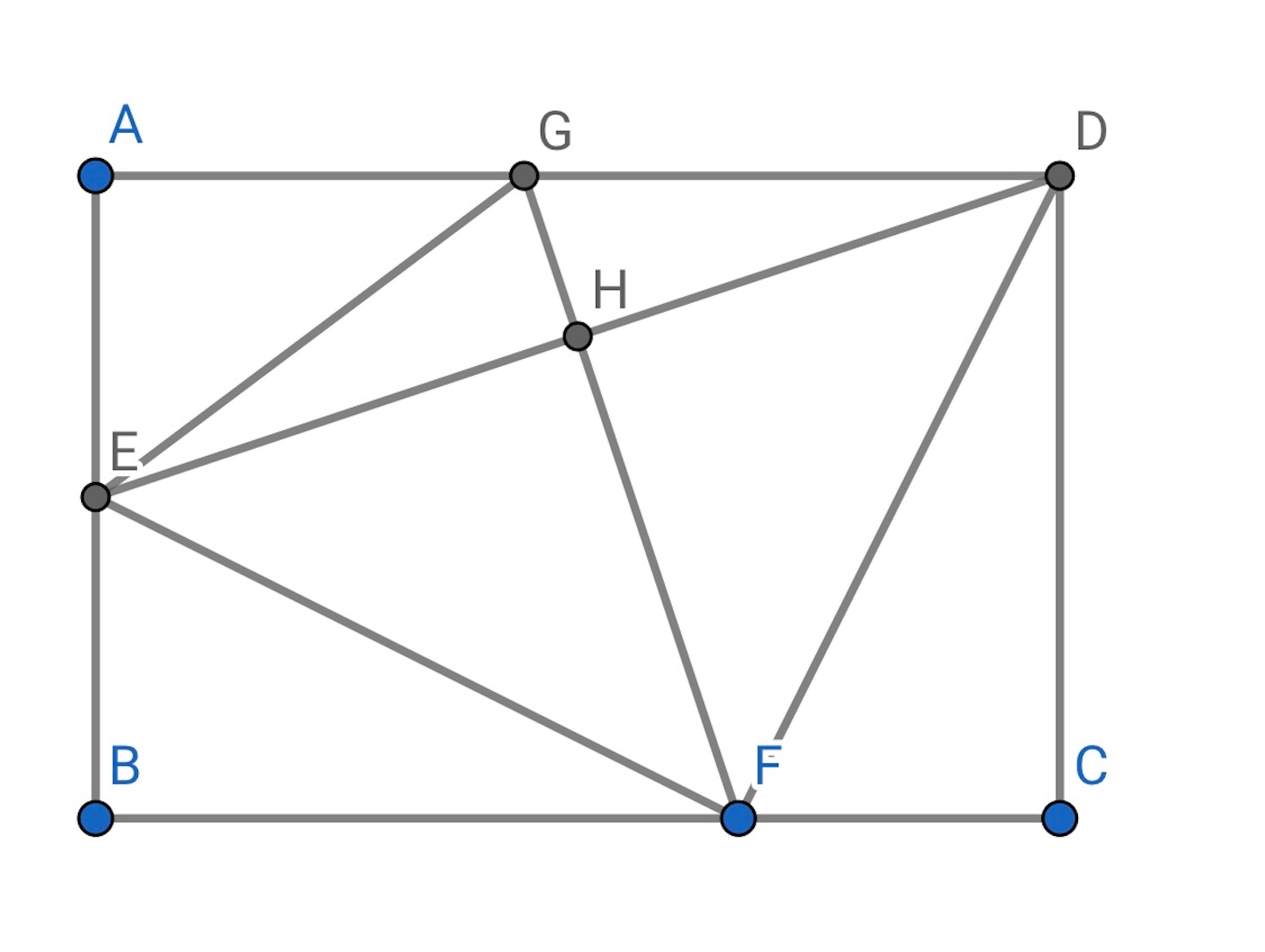
ピタゴラスの定理より,
とおくと,
から,
これを解いて,
なので,
これから,
である.//
【別解 】
したがって,
これから,
//
【別解 】
四辺形 は円に内接するので, 方べきの定理から,
//
【別解 】
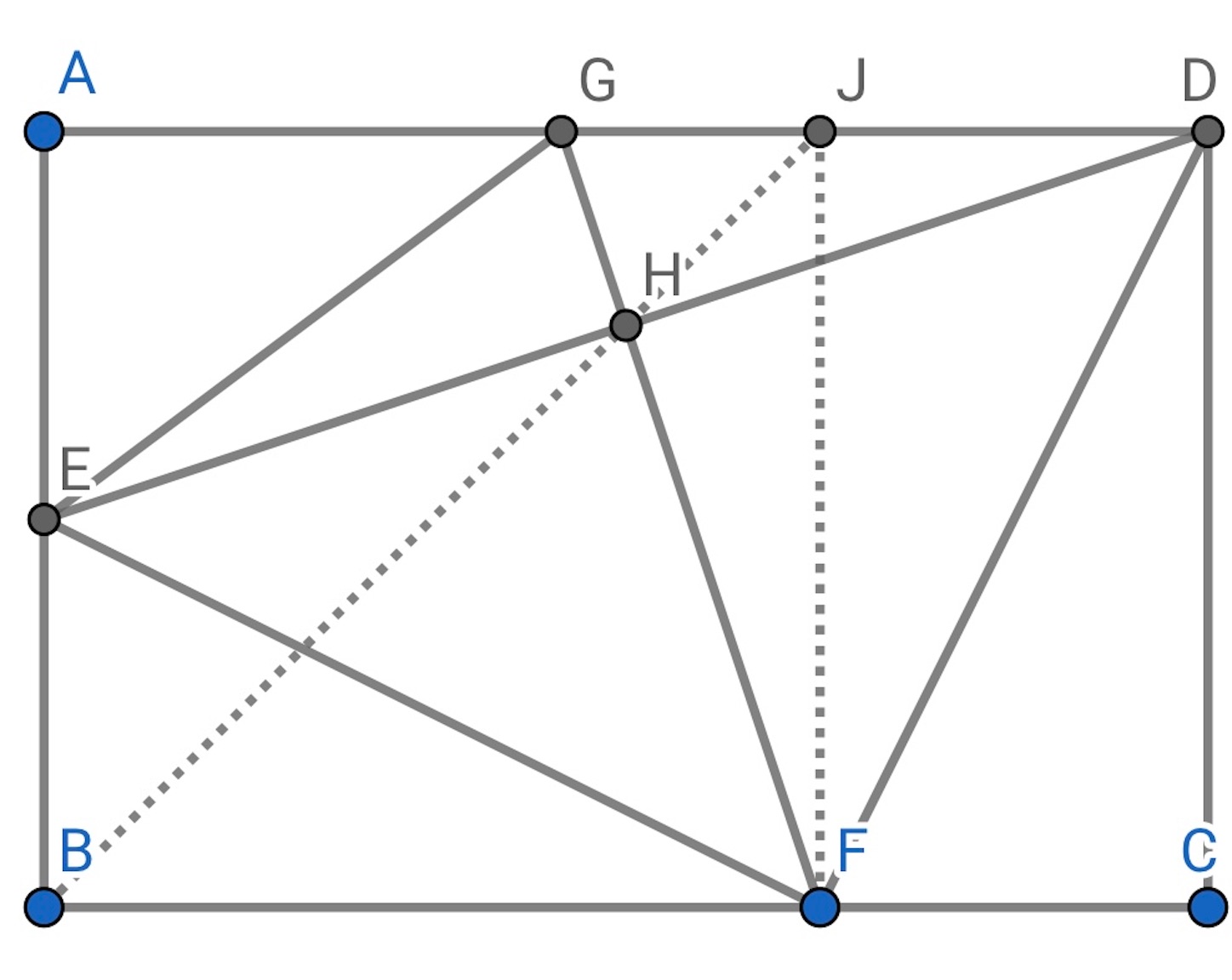
から
に垂線を下ろし, その足を
とする.
は
の外接円の周上にあるので, シムソンの定理により,
,
,
は一直線上にある.
とそれを切る
にメネラウスの定理を使って,
から, である.
と
は相似なので,
である.
なので,
である.//
【別解 】
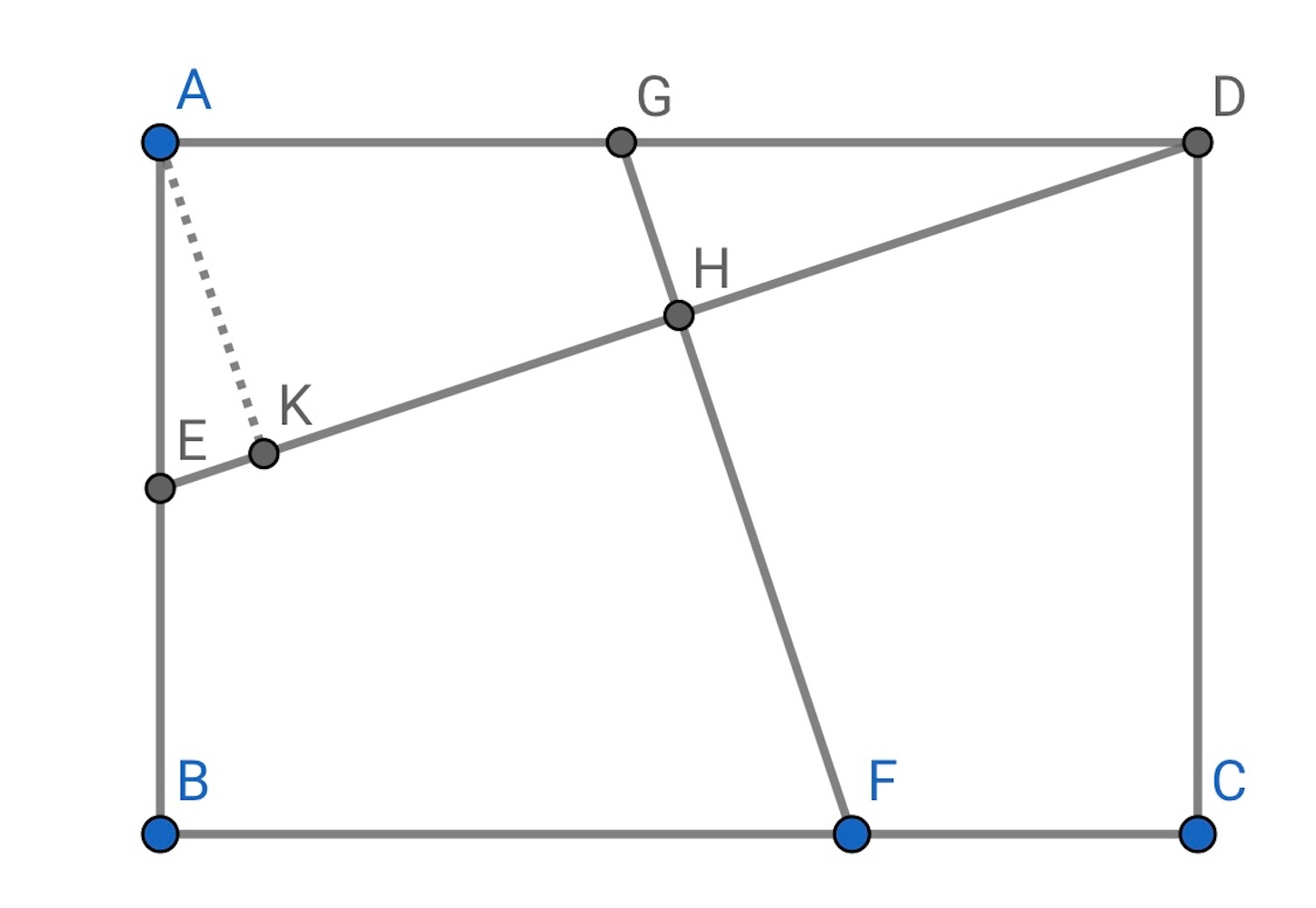
から
に垂線を下ろし, 垂線の足を
とする.
と
は相似なので(もちろん、
と
が相似であることを利用するのが最短であるが……),
と
は相似であることから,
である.//